The best hydraulic section of horizontal-bottomed parabolic channel section＊

Yan-cheng Han (韩延成), Xue-ping Gao (高学平), Zheng-he Xu (徐征和)

1.School of Resources and Environment, University of Jinan, Jinan 250022, China,

E-mail: stu_hanyc@ujn.edu.cn

2.State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China

The best hydraulic section of horizontal-bottomed parabolic channel section＊

Yan-cheng Han (韩延成)1, Xue-ping Gao (高学平)2, Zheng-he Xu (徐征和)1

1.School of Resources and Environment, University of Jinan, Jinan 250022, China,

E-mail: stu_hanyc@ujn.edu.cn

2.State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China

The best hydraulic channel section makes the maximum flow capacity for the same flow cross-area, and the minimum cross-area and wetted perimeter for the same discharge. The construction cost can be reduced nearly to the minimum at the same time. The horizontal bottom parabolic section (HBP section) is a composite section. It is important for design to find the best combination form of the horizontal bottom and the parabolic sides. This paper studies the best hydraulic section and its hydraulic characteristics. The explicit formulae are proposed to determine the dimensions and the best combination form of the horizontal bottom and the parabolic sides. These explicit formulae and the parameters make it easy to design the channel. It is shown that the ratios of the surface width to the depth and the bottom width to the depth are constant for the best hydraulic section. The comparisons with the classic parabolic, rectangular, trapezoid, triangular, semi-cubic and horizontal-bottomed semi-cubic sections show that the HBP section has the largest flow capacity and the shortest wetted perimeter for the same flow area, and has the smallest flow area for the same discharge. It is indicated that the parabolic side parts of the best hydraulic HBP section are different from those of the classic section. The results of the best hydraulic section of the classic parabolic channel cannot be applied directly to the HBC section.

Channel, parabolic shape, horizontal-bottomed, best hydraulic section

Introduction

The best hydraulic cross-section makes the largest flow capacity for a given cross-area. In other words, the cross-area or the wetted perimeter is the minimum for a given conveyance capacity. It can reduce the construction cost nearly to the minimum at the same time[1]. Therefore, the best hydraulic section is always a focus of research. Chow[2]described the explicit formulae of the best hydraulic section for semi-circle, trapezoid, rectangular, parabolic, catenary sections, which helps greatly the designer. Anwar and Clarke[3,4]introduced the freeboard as an additional parameter to be taken into account when designing a power-law channel. Huang et al.[5]proposed a method to design the stable channel using the minimum principle for the river power. It is shown that the shape of the stable channel is circular. Vatankhah[6]presented a type of semi-regular polygon sections such as semi-square, semi-hexagon and semi-octagon sections, and a general solution for the best hydraulic section. Han[7]presented a channel section with horizontal bottom and semi-cubic parabolic shaped sides, deduced the parameters and formula for the best hydraulic section. Wen and Li[8]proposed the hydraulic calculation formula for the horseshoe II type cross-section with flat bottom. Babaeyan-Koopaei et al.[9]proposed a parabolic bottomed triangular shape section using the Lagrange’s multiplier method. Abdulrahman[10]considered a composite channel section with a lower trapezoidal section and an upper rectangular section. Froehlich[11]presented the most hydraulically efficient lined channel. Liu et al.[12]presented an optimal hydraulic section of the compound channel with horizontal bottom and vertical sides. Lu et al.[13]studied thehydraulic characteristics and the best hydraulic section of the U shaped section. Mohanty and Khatua[14]studied the discharge and its distribution in compound channels. Han et al.[15]deduced the formulae of the best hydraulic section for the ice-covered trapezoidal channel. Maleki and Khan[16]evaluated the effect of different channel shapes for accuracy and efficiency of the open channel flow.

There are varieties of forms of the channel section. The parabolic section is one of them. It was suggested[17,2,7]that the unlined canals and the irrigation furrows all might be approximated by a stable parabolic shape. Therefore, the channels can be made more hydraulically stable by initially constructing them in a parabolic shape. It was shown[18,19]that the discharge capacity of a parabolic section is larger than that of a trapezoid section under the same conditions. The cost of the former is less than the latter[20].

The horizontal bottomed parabolic section is composed of a horizontal bottom and two parabolic sides. There are three issues to be considered. The first one concerns the best combination form of the bottom and the sides. The second one concerns the flow capacity under the best hydraulic condition as compared with the classic parabolic section. The third one concerns the possibility of direct applications of the best hydraulic section of the classic parabolic section to the horizontal bottomed parabolic section.

In this paper, the best hydraulic section and the explicit equations are derived to be used to directly calculate the dimensions of the horizontal-bottomed parabolic section. The comparisons with the classic parabolic section and other types of sections are presented.

1. The classic parabolic section

The shape of the classic parabolic section (as shown in Fig.1) is defined by

Fig.1 Classic parabolic section

From Fig.1, it follows that, ifthenTherefore,can be computed by

The flow area and the wetted perimeter can be deduced using the integration method[19,21], as

Fig.2 Horizontal-bottomed parabolic section

2. Characteristics of horizontal-bottomed parabolic section

The horizontal-bottomed parabolic section (as shown in Fig.2) can be expressed by

Obviously, the flow area and the wetted perimeter of the horizontal-bottomed parabolic section can be obtained from the results of the classic parabolic section.

3. Optimum hydraulic section of horizontal-bottomed parabolic section

3.1Characteristics of the best hydraulic section

The discharge of the uniform flow is expressed using the Manningʼs formula as[2]

With dimensionless variables,in Eq.(7) andin Eq.(8) become

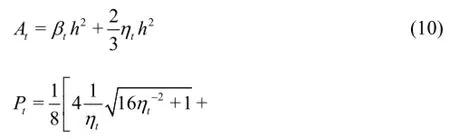
Equation (10), Eq.(11) and Eq.(9) indicate thatcan be determined by

According to the definition of the channel optimum hydraulic section, the best hydraulic section is the type of shape with the maximum discharge for a given area or with the minimum flow area for a given discharge. So the optimization model can be defined by

Based on the Lagrange’s multiplier optimization method, the optimal problem can be described as

From Eq.(12b), the first partial derivative ofΦwith respect to the variablesare expressed as

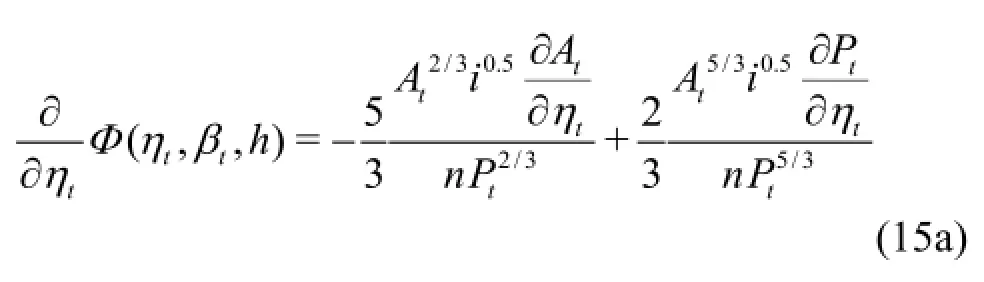
Substituting Eq.(15a) and Eq.(15b) into Eq.(14a) and simplifying, we have

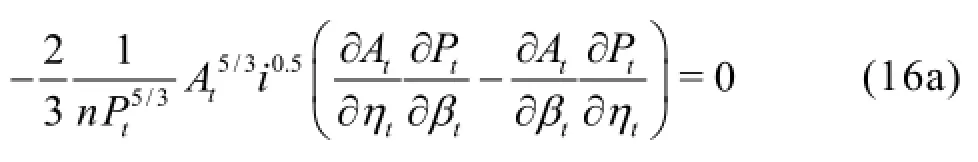
In the same way, substituting Eq.(15a) and Eq.(15c) into Eq.(14b) results in

Therefore, the conditions for the optimal hydraulic section of the horizontal-bottomed parabolic section become

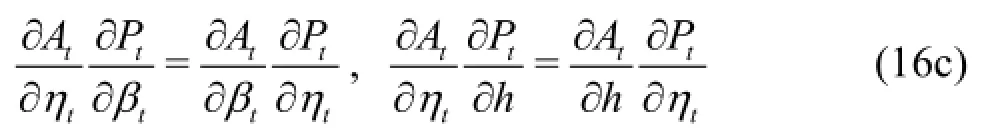
From Eq.(10) and Eq.(11), the partial derivatives ofwith respect to the variablesandhare:

Substituting Eq.(17) into Eq.(16c), after simplifying, the following expression is obtained:

Using the bisection root finding method or the Newton iterative method to solve the first equation of Eqs.(18), the parameterof the best hydraulic section of the horizontal-bottomed parabolic section can be obtained as

From Eq.(19) and Eq.(20), one obtains

Equation (19), Eq.(20) and Eq.(21) describe the best combination form using the horizontal bottom and parabolic shape sides.

3.2Explicit formulae of the best hydraulic section for design

In design, it is often required to compute the discharge when the section dimensions are known. Now letin Eq.(2), Eq.(10) and Eq.(11), the explicit formulae of the optimum hydraulic section forcan be deduced as

Sometimes, it is necessary to calculate the dimensions such asfor a known flow discharge. From Eq.(25), the normal water depthfor the best hydraulic section can be obtained firstly

Then using the relationships:andthe values ofcan be obtained.

Substituting Eq.(26a) into Eq.(6), Eq.(7) and Eq.(8), the following formulae forare obtained as

These parameters (Eq.(19) to Eq.(22)) and the explicit equations(Eq.(23) to Eq.(26d)) are easy to use for the design of the best hydraulic section.

3.3The normal depth and the critical depth of the best hydraulic section

Obviously, Eq.(26a) is the explicit formula for the normal depth of the best hydraulic section.

The general critical equation is expressed as[2]

Substituting Eqs.(7) and (21) into Eq.(26e), the critical depthis obtained as

3.4Verification by using numerical optimization method

For verifying the results of the best hydraulic section from another angle, the optimization variables are set as, according to the definition of the best hydraulic section and Eq.(2), Eq.(7) and Eq.(8), The numerical optimization model can be expressed as wherecan be computed by Eq.(8).

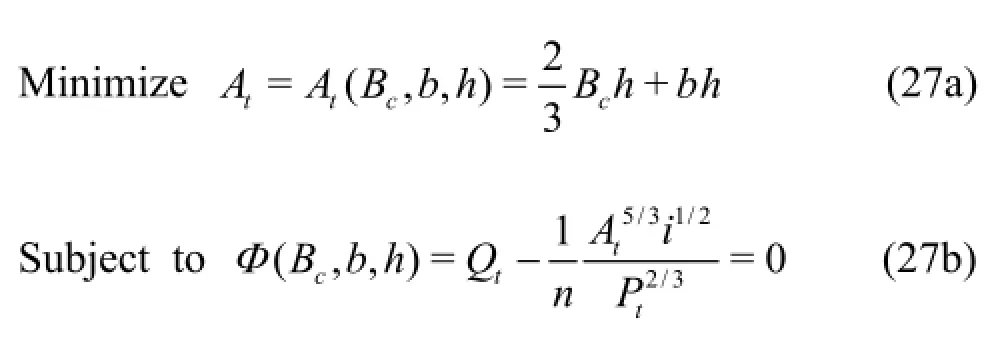
Here, the optimization algorithm of the sequential quadratic programming (SQP) is adopted to verify the above analytical solution. The initial values ofare limited to any values in the range of. It is shown that for any initial values ofthe final optimization result is the same, as Eq.(19) and Eq.(20).

3.5Examples

Example 1: A channel of the designed water depth of 2.2 m, the bed roughness of 0.014, and the bottom slope of 1/12 000. Now we make this channel to have the largest flow capacity for the same flow area.

From Eq.(20) and Eq.(21), one can obtain the bottom width, and the total water surface. From Eq.(22), the shape factor is obtained. From Eq.(23) and Eq.(24), one can obtain the flow area, the wetted perimeter

Example 2: A channel of the flow discharge of 9.0 m3/s, the bed roughness of 0.014, and the bottom slope of 1/15 000. Now we design a channel having the largest flow capacity for the same flow area.

From Eq.(26a) and Eqs.(19) through (22), one obtains the normal water depththen

Secondly, with all known values in Eq.(26c) and Eq.(26d), the flow area and the wetted perimeter are obtained as

We have solved these two examples also by using the nonlinear optimization method. The results are the same as above. However, it is much easier using these analytical solutions, the explicit parameters and the formulae to design the channels than using the nonlinear optimization method.

4. Comparison with classic parabolic shaped section

4.1Best hydraulic section of classic parabolic shaped section

In Fig.2, with the dimensionless variable(Eq.(4)) of the classic parabolic section become

From Eq.(28a) and Eq.(28b), the area and the wetted perimeter can be determined byandin the classic parabolic section. In the same way, using the Lagrange’s multiplier method, the condition for the best hydraulic section is

From Eq.(27) and Eq.(28), the partial derivatives ofandwith respect to the variablesare

Substituting Eq.(30) into Eq.(29), the following equation is obtained

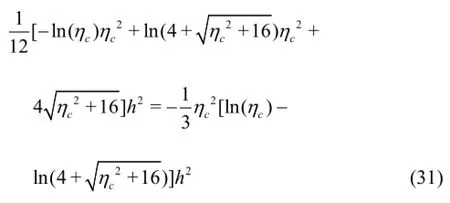
Solving Eq.(31) , the value ofof the best hydraulic section for the classic parabolic section is obtained

Substituting Eq.(32) into Eq.(2), Eq.(27) and Eq.(28), the explicit formulae forare obtained

Substituting Eq.(34) and Eq.(35) into the uniform flow formulathe relationship betweenfor the classic parabolic best hydraulic section is obtained as

The normal water depth under the best hydraulic section conditions can be computed by

Substituting Eq.(37a) into Eq.(32), Eq.(34) and Eq.(35), the explicit equations for design are obtained for a given discharge

4.2Best hydraulic section of trapezoid section

It is known that the ratio of the bottom width to the depth isfor the best hydraulic section of the trapezoid section. Whenthe flow discharge is the maximum[2]. Using the same method, the characteristics of the best hy draulic section for the trapezoid section can be ob tained (as listed in Table 1).

4.3Comparison with classic parabolic section and trapezoid section

From Eqs.(19) through (26d) and the comparisons listed in Table 1, it follows that

Table 1 Properties of the best hydraulic section for trapezoid, classic parabolic and HBC sections

Table 2 The best hydraulic section of trapezoid, HBP and HBC sections for Example 1

(1) The water depth flow area, the wetted perimeter and the water surface width of the horizontalbottomed parabolic section are all smaller than those of the classic parabolic and trapezoid sections for a given flow discharge for the best hydraulic section.

(2) It is indicated that for a given area or wetted perimeter, the flow discharge of the HBC section is larger than that of the classic parabolic and trapezoid sections.

4.4Applications

Example 1: A canal with parabolic sides and horizontal bottom with the bed roughnessthe bottom slopeand the water depth1.5 m. Now it is necessary to design the best hydraulic section, and calculatethen compare the results with those of the classic parabolic section.

(1) The results of the section with horizontal bottom and parabolic sides

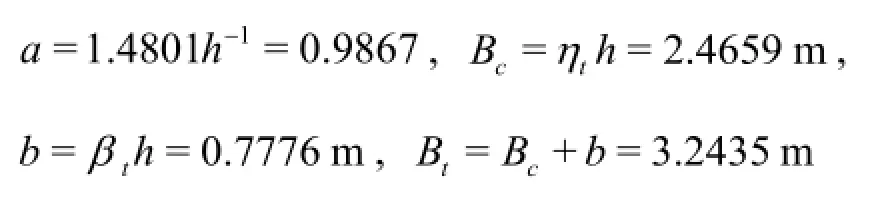
Then substituting all known values into Eqs.(22) through (25), we obtain

(2) The results of classic parabolic section

Substituting all known values into Eq.(32) and Eq.(33), we have

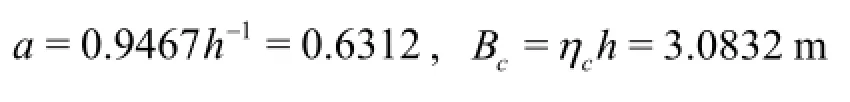
Similarly, substituting all known values into Eqs.(34) through (36), we obtain

The results are listed in Table 2.

Example 2: A channel with parabolic sides and horizontal bottom withNow design a channel using the best hydraulic section method.

(1) The results of using horizontal bottom parabolic section

Firstly, substituting the flow discharge and other known values into Eq.(26a) and Eqs.(19) through (22). The water depthand other dimensions can be calculated:

Secondly, substituting all known values into Eq.(26c) and Eq.(26d), we obtain

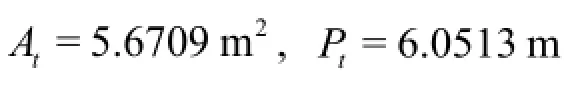
Table 3 The best hydraulic section of trapezoid, HBP and HBC sections for Example 2

Table 4 Properties of best hydraulic section for different types of sections

Table 4 Properties of best hydraulic section for different types of sections

(2) The results of using classic parabolic section

Substituting all known values into Eq.(37a), Eq.(32) and Eq.(33), we have

Secondly, substituting all known values into Eq.(37b), we obtain

The results are listed in Table 3.

The results from two examples show that these explicit formulae are easy to use in the design of the best hydraulic section. The comparisons in the Example 2 show that the flow area and the wetted perimeter of the HBC section are smaller than those of the classic parabolic section.

5. Comparison with other types of sections

In the same way, one can study the characteristics of the rectangular, trapezoid, triangular, semi-cubic and horizontal-bottomed semi-cubic sections under the best hydraulic conditions. The comparisons between the horizontal-bottomed parabolic section and other nine types of sections are listed in Table 4.

The comparisons show that the flow area and the wetted perimeter of the HBC section are the smallest among all seven types of sections listed in Table 4 for the same discharge. In other words, the discharge is the largest for a given flow area. The construction cost of the channel is mainly related with the earthwork excavation, lining and land requisition expenses. In general, the land requisition accounts for a small proportion. Therefore, the HBC section is an economic section.

6. Conclusions

To find the best combination form of the horizontal bottom and parabolic sides is important for the design of the horizontal bottom parabolic channel section. In this paper, the section parameters and the explicit formulae of the best hydraulic section are derived and can be used to calculate the channel dimensions directly. It is shown that the ratio of the horizontal bottom to the water depthis 0.5184, the ratio of the total water surface width to the water depthis 2.1623, the product of the shape factor and the water depthis 1.4801. The comparisons with othernine types of sections (the classic parabolic, rectangular, trapezoid, triangular, semi-cubic and horizontalbottomed semi-cubic sections) show that the HBP section has the largest flow capacity and the shortest wetted perimeter for the same flow area. On the other hand, it has the smallest flow area for the same discharge. Comparing the shape parametersit is shown that the parametersof the classic parabolic and HBC sections are different. Therefore, the side shape of the best hydraulic section of the classic parabolic section cannot be applied directly to the horizontal bottomed parabolic section.

[1] Jain A., Bhattacharya R. K., Sanaga S. Optimal design of composite channels using genetic algorithm [J].Journal of Irrigation and Drainage Engineering, 2004, 130(4): 286-295.

[2] Chow V. T. Open channel hydraulics [M]. New York, USA: McGraw-Hill, 1959.

[3] Anwar A. A., Clarke D. Design of hydraulically efficient power-law channels with freeboard [J].Journal of Irrigation and Drainage Engineering, 2005, 131(6): 560-563.

[4] Anwar A. A., de Vries T. T. Hydraulically efficient powerlaw channels [J].Journal of Irrigation and Drainage Engineering, 2003, 129(1): 18-26.

[5] Huang C. A., Gong M. F., Chen Z. C. et al. Stable channel shape based on the principle of minimum stream power [J].Journal of Hydrodynamics, Ser. A, 2005, 20(2):189-195 (in Chinese)

[6] Vatankhah A. R. Semi-regular polygon as the best hydraulic section in practice (generalized solutions) [J].Flow Measurement and Instrumentation, 2014, 38: 67-74.

[7] Han Y. C. Horizontal bottomed semi-cubic parabolic channel and best hydraulic section [J].Flow Measurement and Instrumentation, 2015, 45: 56-61.

[8] Wen H., Li F. L. Hydraulic calculation of horseshoe crosssection with flat-bottom [J].Transactions of the Chinese Society of Agricultural Engineering, 2013, 29(10): 130-135.

[9] Babaeyan-Koopaei K., Valentine E. M., Swailes D. C. Optimal design of parabolic-bottomed triangle canals [J].Journal of Irrigation and Drainage Engineering, 2000, 126(6): 408-411.

[10] Abdulrahman A. Best hydraulic section of a composite channel [J].Journal of Hydraulic Engineering, ASCE, 2007, 133(6): 695-697.

[11] Froehlich D. C. Most hydraulically efficient standard lined canal sections [J].Journal of Irrigation and Drainage Engineering, 2008, 134(4): 462-471.

[12] Liu H. Y., Zhang X. Y., Sun D. H. et al. Design of optimal hydraulic section and economic practical section for compound canal [J].Journal of Water Resources and Water Engineering, 2006, 17(4): 89-91(in Chinese).

[13] Lu H. X., Zhou W. B., Liu H. J. Hydraulic characteristics and hydraulic calculation of U-shaped channel [J].Journal of Irrigation and Drainage, 2004, 23(4): 50-52(in Chinese).

[14] Mohanty P. K., Khatua K. K. Estimation of discharge and its distribution in compound channels [J].Journal of Hydrodynamics, 2014, 26(1): 144-154.

[15] Han Y. C., Xu Z., Easa S. M. et al. Optimal hydraulic section of ice-covered open trapezoidal channel [J].Journal of Cold Regions Engineering, 2017, 06017001.

[16] Maleki S. F., Khan A. A. Effect of channel shape on selection of time marching scheme in the discontinuous Galerkin method for 1-D open channel flow [J].Journal of Hydrodynamics, 2015, 27(3): 413-426.

[17] Mironenko A. P., Willardson L. S., Jenab S. A. Parabolic canal design and analysis [J].Journal of Irrigation and Drainage Engineering, 1984, 110(2): 241-246.

[18] Chahar B. R. Optimal design of parabolic canal section [J].Journal of Irrigation and Drainage Engineering, 2005, 131(6): 546-554.

[19] Han Y. C., Easa S. M. Superior cubic channel section and analytical solution of best hydraulic properties [J].Flow Measurement and Instrumentation, 2016, 50: 169-177.

[20] Easa S. M. Improved channel cross section with two-segment parabolic sides and horizontal bottom [J].Journal of Irrigation and Drainage Engineering, 2009, 135(3): 357-365.

[21] Chahar B. R. Optimal design of a special class of curvilinear bottomed channel section [J].Journal of Hydraulic Engineering, ASCE, 2007, 133(5): 571-576.

(Received April 23, 2015, Revised July 4, 2015)

* Project supported by the Key Research and Development Program of Shandong Province (Grant No. 2016GSF117038), the National Science and Technology Support Program of China (Grant No. 2015BAB07B02), the Development of Science and Technology Plan of Jinan City, China (Grant No. 201302052), and the Teaching and Research Projects of the University of Jinan (Grant No. J1641).

Biography: Yan-cheng Han (1971-), Male, Ph. D.,

Associate Professor