基于一种渐进半软阈值函数的小波去噪*

2017-04-25吴安全沈长圣肖金标孙小菡

电子器件 2017年2期

关键词：方根小波信噪比

吴安全,沈长圣,肖金标,孙小菡

(东南大学电子器件和系统可靠性研究中心,南京 210096)

基于一种渐进半软阈值函数的小波去噪*

吴安全,沈长圣*,肖金标,孙小菡

(东南大学电子器件和系统可靠性研究中心,南京 210096)

针对硬软阈值函数的不足,提出了一种渐进半软阈值函数,不仅弥补了硬阈值函数不连续性的缺陷,同时还克服软阈值函数重构信号后存在恒定偏差的缺陷,使得估计的小波系数逐渐接近于真实小波系数。通过对含噪Doppler信号的MATLAB仿真实验结果表明,与传统阈值函数和几种改进阈值函数相比,渐进半软阈值函数在去噪性能上能够获得更优的信噪比(SNR=21.443 1 dB)和均方根误差(RMSE=0.343 3),更适合于实际应用。

信号处理;小波变换;阈值去噪;信噪比;均方根误差

通信系统中的各种电子设备和信道,都有轻重不同的噪声源,影响着有用信号的传输,在实际工程中,为了提取和分析信号的有用信息,对受污染的信号进行去噪是非常重要的;通信系统中的包含的有用信号以及各种噪声信号,具有非线性,非平稳的特性,小波变换因具有时频域局部化的能力和良好多分辨率分析的特性是分析分析这类信号的有力工具。经过二十几年的发展,而小波变换已经被证明是在信号去噪方面的一种非常有效的方法,并且应用范围越来越广泛[1-2]。

在小波去噪方法中,小波域的阈值去噪法是一种简单常用的技术,然而传统的硬阈值[3]和软阈值[4]存在一些不足:硬阈值函数使得小波系数在阈值位置处是不连续的,导致重构的信号振荡;而软阈值函数有更好的连续性,但是原来的小波系数和噪声信号的阈值小波系数之间存在恒定的偏差。为了克服硬软阈值的缺点,提出了一种渐进半软阈值函数,与原来的阈值函数相比,渐进半软阈值函数,不但同软阈值函数一样是连续的,而且不存在恒定的偏差。

一个含噪的一维信号模型可表示为如下形式:

x(k)=s(k)+ε(k)k=1,2,…,n

(1)

式中:x(k)为含噪信号,s(k)为有用信号,ε(k)为噪声信号,k为信号的数目。ε(k)通常表现为高频信号,而实际工程中s(k)为相对低频信号或者是一些比较平稳的信号。

小波阈值去噪过程如图1所示。(1)对含噪信号进行N层的小波分解;(2)对高频系数能够阈值处理;(3)信号的小波重构。

图1 小波去噪过程示意图

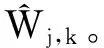
硬阈值函数是当某位小波变换值大于给定阈值时,保持不变,而小于给定阈值时变为零,其表达式如下:

(2)

软阈值函数是当某位小波变换值大于给定阈值λ时,向着减小系数幅值的方向作一个收缩λ;而小于给定阈值λ时,变为零,其表达式如下:

(3)

尽管硬阈值和软阈值在实际的信号处理得到了广泛的应用[5-6],但是还是存在不足:式(2)所表示的硬阈值函数在λ和-λ处存在间断点,不连续性将导致重构的信号容易产生伪吉布斯现象和一定程度的振动往往有较大的方差。式(3)所表示的软阈值函数有较好的连续性,不会产生额外的振荡,但是在估计的小波系数和原始小波系数间存在恒定的偏差;重构信号后,将会失去一些有用的高频信号,这会导致重构信号的信噪比较低,均方根误差较大;软阈值函数导数的不连续性也将直接影响重构信号与真实信号的逼近程度[7-8]。

1 渐进半软阈值函数

针对硬阈值和软阈值函数的不足,提出了一种渐进半软阈值函数,其函数表达式如下:

(4)

当小波系数的绝对值小于或等于阈值时,同传统阈值函数一样,将其全部置零;当小波系数的绝对值大于阈值时,小波系数收缩。如图2所示,该函数在小波域内是连续的,弥补了硬阈值函数存在间断点的不足,重构的信号不存在振荡的情况。

考察函数:

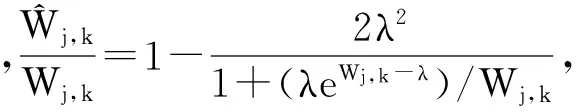
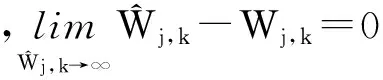
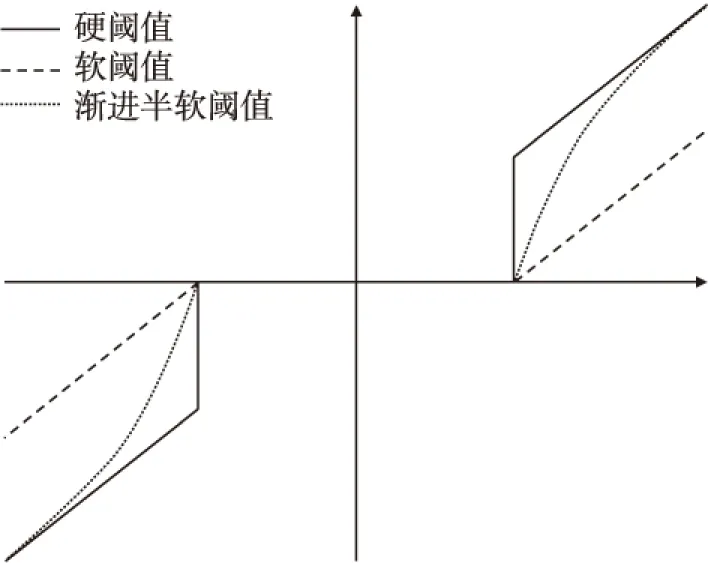
图2 硬阈值、软阈值和渐进半软阈值函数的比较

2 仿真结果及讨论

为了验证新渐进半软阈值函数的有效性,除了硬软阈值函数以外,并与其他3种阈值函数法进行比较:GaoHongYe提出的Garrote函数[9],文献[10-11]提出的改进阈值函数,其表达式分别为

函数1[9]:

(5)

函数2[10]:

(6)

函数3[11]:

(7)

去噪性能的指标通常是用去噪后的信噪比(SNR)与均方根误差(RMSE)进行评价的,SNR和RMSE表达式分别为

(8)

(9)

基于MATLAB平台对含有高斯白噪声的Doppler信号进行仿真实验,采样点数N=1 024;同时将渐进半软阈值函数与硬阈值,软阈值,文献[9-11]中分别提出的阈值函数,这里选用sym6小波,分解层数为5层,阈值λ的获取是基于Minimax算法[12].

不同阈值函数对含有SNR=12.299 8dB的高斯白噪声的Doppler信号进行仿真实验得到如图3和表1的实验结果。

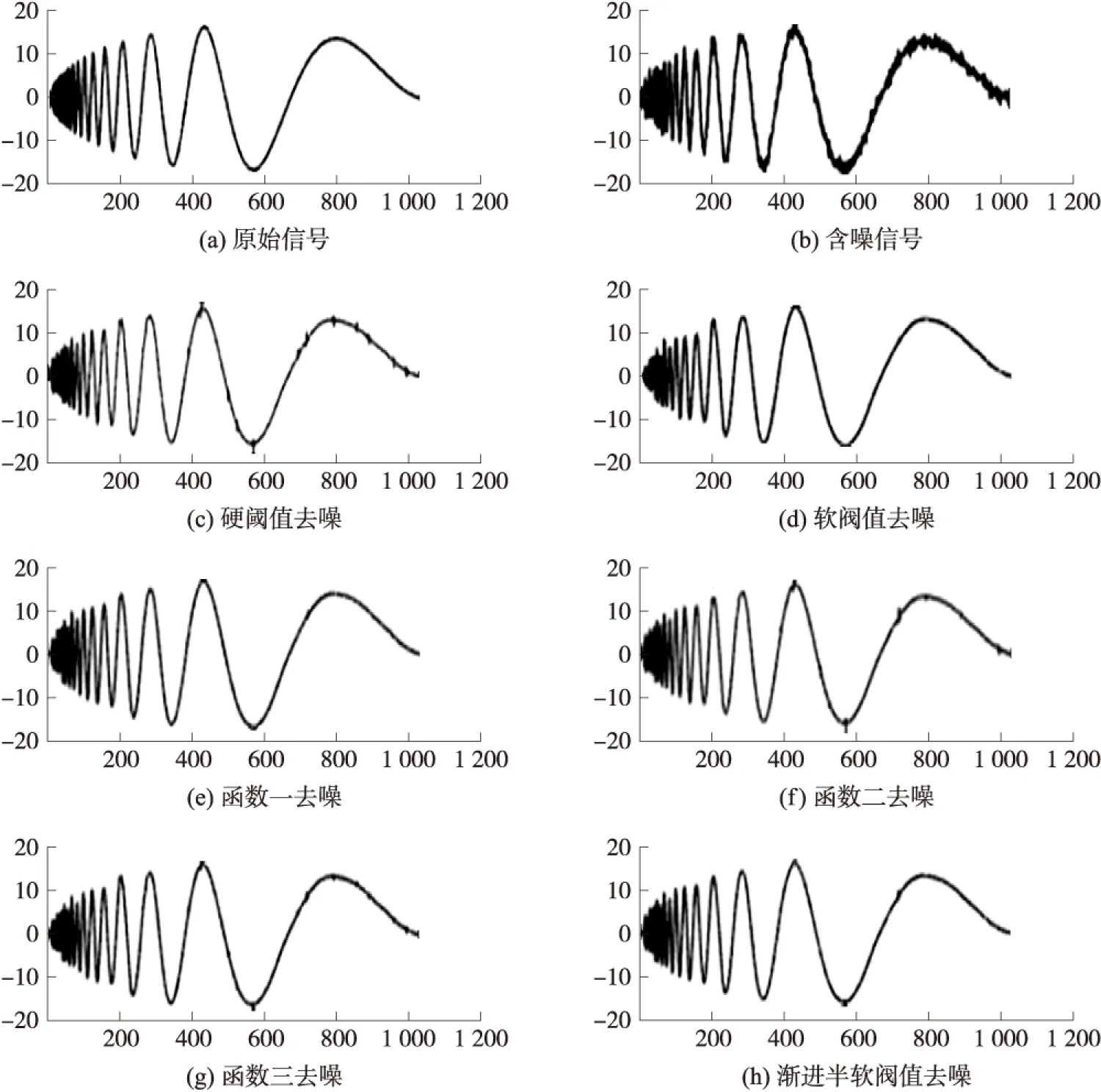
图3 不同阈值函数对含噪Doppler信号去噪

表1 去噪后的信噪比与均方根误差

从图3和表1可以看出,几种阈值函数都能较好的去掉信号中的噪声。但是硬阈值函数去噪后的波形有较多的振荡点,而软阈值函数去噪后虽然光滑,但信噪比较低。而其他3种改进阈值函数虽然信噪比较高,但都有较多的振荡点;渐进半软阈值函数无论在SNR增益还是RMSE上都是最优的。

分别对加入不同信噪比高斯白噪声Doppler信号进行去噪处理,对去噪后得到了SNR和均方根误差比较,得到如图4所示的实验结果。

图4(a)和图4(b)的横坐标为去噪前的信噪比,纵坐标分别为去噪后相应的SNR和RMSE。由图4可以看出,无论是低信噪比还是高信噪比中,相较于硬阈值,软阈值,文献[9-11]中分别提出的阈值函数,渐进半软阈值函数去噪后获得的SNR增益和RMSE上均使最优的。

图4 不同信噪比下的去噪性能对比

3 结论

在分析传统小波阈值函数存在的固有缺点的基础上,提出了一种渐进半软阈值函数。通过半软阈值函数与硬阈值,软阈值,文献[9-11]中分别提出的阈值函数,对Doppler信号去噪效果的比较证明,渐进半软阈值函数量化得到的重构信号最接近原始信号,并且弥补了硬阈值函数的不连续和不完全去除噪声的缺陷,同时又克服了软阈值函数具有恒定偏差的缺点,具有较高的实用价值。

[1] Alshamali A. Wavelet Based ECG compression with Adaptive Thresholding and Efficient Coding[J]. Journal of Medical Engineering and Technology,2010,34(5/6):335-339.

[2] Zhang Shuqi,Li Jinzhong. Guo Rui,et al. Study on White Noise Suppression Using Complex Wavelet Threshold Algorithm[J]. Applied Mechanics and Materials,2014,521:347-351.

[3] Donoho D L,Johnstone I M. Ideal Spatial Adaption Via Wavelet Shrinkage[J]. Biometrika,1994,81(12):425-455.

[4] Donoho D L. De-Noising by Soft Thresholding[J]. IEEE Transactions on Information Theory,1995,41(3):613-627.

[5] Chen Cheng,Zhou Ningning. A New Wavelet Hard Threshold to Process Image with Strong Gaussian Noise[C]//Proc of the 5th International Conference on Advanced Computational Intelligence. Nanjing:IEEE.2012:558-561.

[6] Phu Ngoc Le,Ambikairajah Eliathamby,Choi Eric. An Improved Soft Threshold Method for DCT Speech Enhancement[C]//Proc of the 2nd International Conference on Communications and Electronics. 2008:68-271.

[7] Qian Sumin,Zhang Linxu,Zhang Yun,et al. Study of De-Nosing Improved Based on Wavelet Threshold[J]. Foreign Electronic Measurement Technology,2012,31(5):49-51.

[8] Ren Zhong,Liu Ying,Liu Guodong,Huang Zhen. Improved Wavelet Denoising with Dual-Threshold and Dual-Factor Function[J]. Journal of Computer Applications,2013,33(9):2595-2598.

[9] Gao Hongye. Wavelet Shringkage Denoising Using the Non-Negative Garrote[J]. Journal of Computational and Graphical Statistics,1998,7(4):469-488.

[10] 许后磊,储冬冬. 基于改进阈值的提升小波变换在探地雷达信号去噪中的应用[J]. 三峡大学学报(自然科学版),2010,32(2):42-47.

[11] Zhao Qiming,Dai Wenzhan. A Wavelet Denoising Method of New Adjustable Threshold[C]//Proc of the 16th International Conference on Communication Technology(ICCT). Hangzhou:IEEE,2015:684-688.

[12] Gao Hongye,Bruce A G. Wave Shrink with Semisoft Shrinkage[J]. Statistica Sinica,1997(7):855-874.

Wavelet Denoising Based on an Asymptotic Semisoft Thresholding Function*

WUAnquan,SHENChangsheng*,XIAOJinbiao,SUNXiaohan

(Research Center for Electronic Device and System Reliability,Southeast University,Nanjing 210096,China)

For defect of the hard and soft threshold function,a semisoft threshold function is proposed. The function not only compensates for that the defect of the hard threshold function is not continuous,but also overcome the problem of that the soft threshold function exists constant bias in reconstructed signal. The semisoft threshold function makes the estimated wavelet coefficients of the wavelet coefficients gradually closer to the real. The results of MATLAB simulations show that Doppler affected by noise can get better SNR which is 21.443 1 dB and RMSE which is 0.343 3 on de-noising performance,compared with the traditional threshold functions and several improved threshold function. Therefore,it is more suitable for practical applications.

signal processing;wavelet transform;threshold de-noising;SNR;RMSE