LMS自适应滤波器模块化设计及其FPGA实现*

2017-04-25靳宝全王云才安光峡

电子器件 2017年2期

关键词：调用权值模块化

雷宇,靳宝全*,王云才,安光峡,王宇,王东

(1.太原理工大学新型传感器与智能控制教育部重点实验室,太原 030024;2.山西煤层气(天然气)集输有限公司,太原 030032)

LMS自适应滤波器模块化设计及其FPGA实现*

雷宇1,靳宝全1*,王云才1,安光峡2,王宇1,王东1

(1.太原理工大学新型传感器与智能控制教育部重点实验室,太原 030024;2.山西煤层气(天然气)集输有限公司,太原 030032)

针对LMS自适应滤波器在FPGA上实现结构灵活性的问题,提出了一种模块化设计方法。根据LMS算法结构特点,结合FPGA硬件语言特点进行模块化设计,分别阐述了各模块设计结构,对模块进行并行调用与综合。对模块化设计的自适应滤波器与纯串行及纯并行设计的自适应滤波器所占用的资源以及处理速率进行比较,8个并行模块结构比全串行结构处理速率快了近7.6倍,硬件资源占用比全并行结构减少了近50%;结果说明模块化LMS自适应滤波器设计具有更加灵活的结构特点。

自适应滤波器;模块化设计;最小均方误差准则;现场可编程门阵列

自适应滤波器可以即时调节滤波参数,具有优秀的动态滤波效果。最小均方误差LMS(Least Mean Square)算法广泛应用于自适应滤波器的设计中,已经成为自适应滤波所采用最佳准则的一种。而FPGA芯片时钟频率高、控制周期短、执行速度快、灵活性强[1]、可以满足系统对实时性、高速数据处理的要求[2],在FPGA上实现基于LMS算法的自适应滤波器的方法及结构改进是目前的一个研究热点。

LMS自适应算法为递推式,采用该算法的自适应滤波器硬件实现更为便捷。近几年的研究已经在FPGA上实现了LMS自适应滤波器,并提出改进的延迟LMS自适应滤波器,提高了滤波器的数据吞吐速率[3-4],针对LMS滤波算法收敛性能提出了变步长LMS自适应滤波算法显著改善了收敛性能[5],应用方面利用FPGA设计的LMS自适应滤波器进行飞机机翼的振动主动控制[6]。利用FPGA设计的变步长自适应滤波器进行信号去噪[7];在金属塑性材料细观损伤过程声发射特性得到了良好的实验效果[8]。设计结构方面,有学者在FPGA上对改进后的LMS算法时的处理速率以及逻辑资源占用率进行了实践探究与分析,并利用符号算法节约了自适应滤波器对乘法器资源的利用[9],利用流水线结构设计提高了数据处理速率[10-11]。目前对LMS自适应滤波器在FPGA上实现时结构的探究仍然有待加深,进一步对FPGA实现LMS自适应滤波器时的资源与速率的探究是必要的。

本文在之前研究的基础上,探究利用模块化结构以FPGA为载体设计LMS自适应横向滤波器,提高其在FPGA上的面积与速率交换的灵活性,并且能达到较高的阶数(4～64)。利用Altera公司的EP4CE15F17C8芯片上设计串并结构的滤波器,并对其性能进行了分析。

1 LMS自适应算法硬件实现原理

LMS算法便于硬件结构实现,采用改进均方误差梯度的估计值计算方法[12],算法的逼近过程用式(1)表示:

(1)

由上面一组递推公式,输出信号y(n)等于滤波器系数向量W(n)与输入信号X(n)的积。而滤波器系数向量不断根据误差信号e(n)更新,误差信号为期望信号d(n)与实际输出信号的差。

由推导公式可知LMS自适应滤波器的全并行结构图如图1所示。

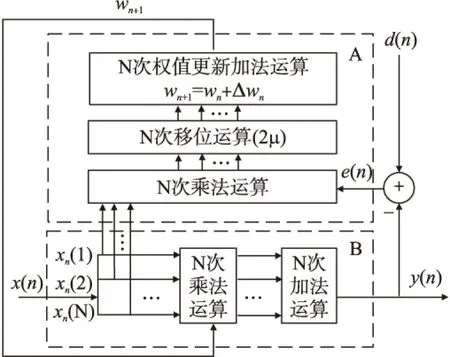
图1 LMS自适应滤波器全并行结构示意图

图1中A虚线框内为LMS权值更新模块,B虚线框内为滤波器模块,LMS自适应滤波器中,权值更新模块以及滤波器模块是相对独立的2个部分。所以,若采用全并行结构进行设计,对于深度为N的滤波器,需要占用2N个乘法器以及较多逻辑资源,而采用全串行结构设计则完成一次权值更新至少需要N个时钟周期,制约了数据处理速率。

在进行FPGA设计时,可以对LMS算法模块化设计,既保证处理速度的同时又能对FPGA逻辑资源进行合理利用。图1中对于LMS自适应滤波器可以分为3个模块组成,多级处理结构如图2所示。

由图2可知,在LMS自适应算法的多级结构中,需要对各模块进行FPGA模块化编程,以及对输入、输出以及误差信号进行同步分配处理。最终组合成为完整的自适应滤波器。

图2 LMS多级处理结构

2 多级LMS自适应滤波器结构

2.1 FIR串行模块的设计

考虑FIR滤波器部分公式(2)

y(n)=WH(n)X(n)

(2)

FIR滤波器串行结构示意图如图3所示。

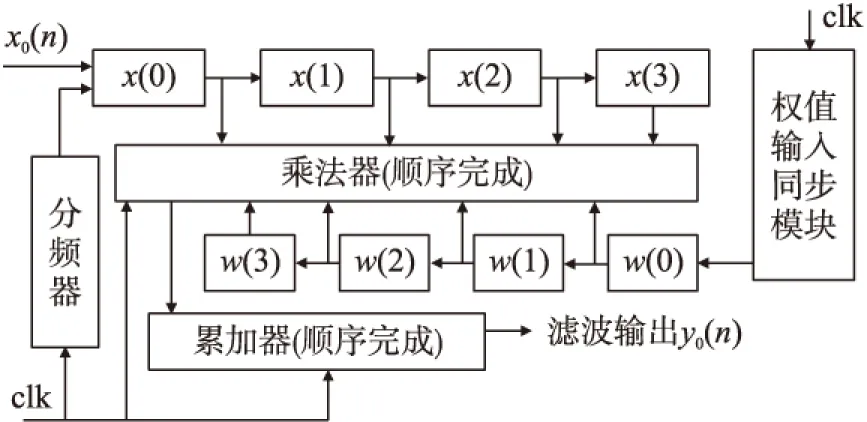
图3 FIR滤波输出串行结构示意图

图3中串行FIR模块需要在时钟控制下顺序完成4次抽头系数的权值更新运算,由于LMS算法中的权值信号不是对称的,不需要进行对称系数加法运算,所以模块内需要调用1个加法器1个乘法器以及1个移位器,每个器件重复调用4次。

定义FIR串行功能模块名为FSMO,它的输入输出配置如下:输入为时钟clk,复位信号rst,以及12位波形信号输入Xin,12位加权系数值输入Win,28位信号输出Yout。

对FIR滤波输出串行模块根据时序以及功能要求进行verilog HDL程序设计,进行行为仿真,仿真结果如图4所示。

仿真中设置数据频率clk_data,为时钟频率clk的4倍,模块仿真输入Xin与Win为MATLAB仿真生成的数据,通过文本文档方式输入到FPGA专用仿真工具Modulesim中进行功能仿真测试。

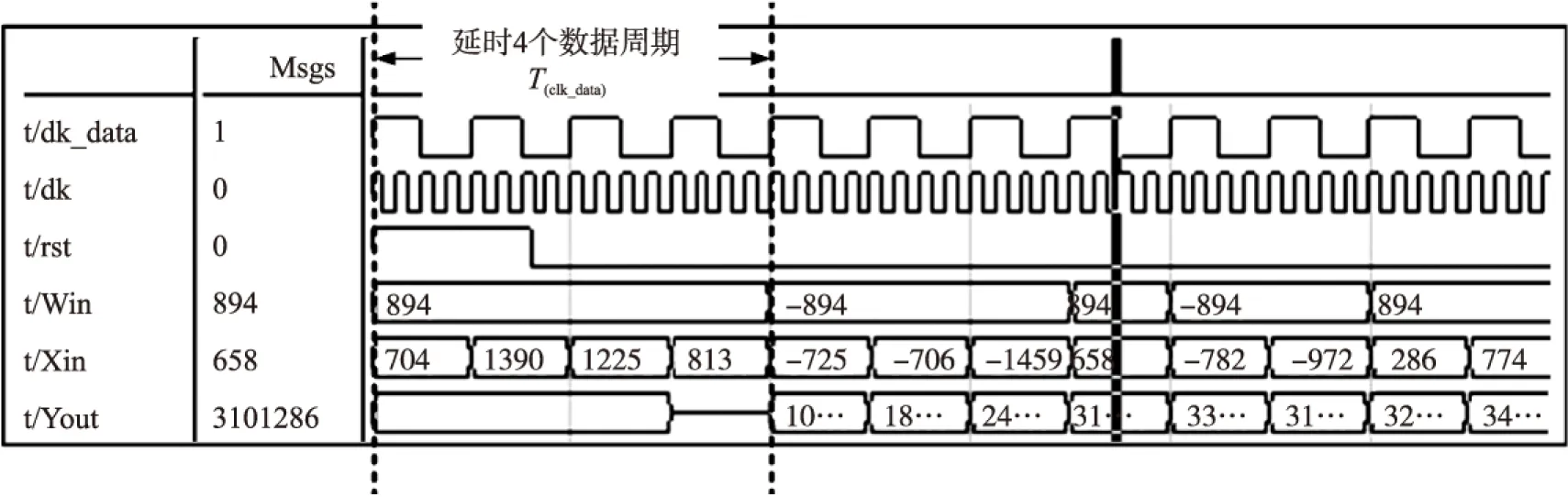
图4 功能模块FSMO时序仿真

由图4可知FIR串行模块实现了权值与输入的四次乘法累加运算,延时4个数据周期(clk_data)后,Yout开始输出。由图中看出输出Yout的值3101286刚好对应从Xin为1225输入到706的与对应系数Win乘积的累加和。仿真结果说明模块功能正确。

2.2 LMS串行模块的设计

LMS串行结构设计如图5所示,要考虑将反馈路径设计为输入接口,将求取误差信号的部分排除,以方便调用。将LMS公式改写为式(3):

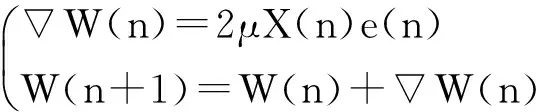
(3)

设计LMS串行模块示意图如图5所示。

图5中权值输入同步模块,根据时钟控制,乘法器模块完成x(n)与e(n)的对应运算并按照时序进行乘μ以及权值更新输出。该模块的接口配置为:输

入时钟clk,复位信号rst,以及与FIR同步的12位波形信号输入Xin,12位拆分好的误差输入error,在进行误差信号处理时,对“error[16:5]”处理以完成移位操作,相当于乘以权值μ=1/64。对权值更新串行模块根据时序以及功能要求进行RTL级程序设计,其仿真图如图6所示。

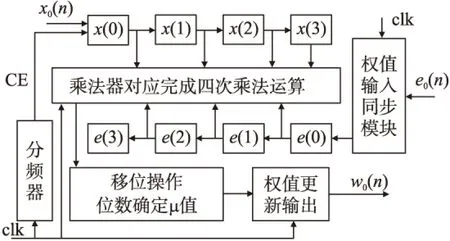
图5 多级LMS算法示意图

图6 功能模块LMSC时序仿真

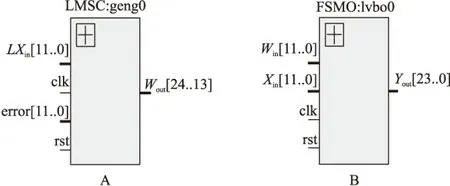
图7 最终设计LMSC模块以及FSMO模块

最终设计的2个模块FSMO以及LMSC的封装RTL(Register-Transfer Level)级视图如图7所示。

图7中A为LMS权值更新模块,B为FIR串行模块,A模块以及B模块中的输入LXin与Xin引脚输入原始信号数据,error输入式(1)中求取的误差信号e(n)数据,Win输入不断更新的权值数据,数据位数均为12位字长的数据。输出接口Wout输出更新好的权值数据,需要进行高位截位处理,B模块中输出Yout为单个模块的滤波结果。

2.3 LMS多级处理结构整体设计

由图2可知,多级处理结构在并行调用串行模块时,要将输入输出数据进行同步分组和组合,以求取误差值以及最终的滤波输出结果。

以15阶自适应FIR滤波器,12位系数量化位数,12位位宽输入信号,输出数据为25比特,参考信号以及误差信号量化位数均为12位的模块化设计为例,其并行模块通过例化并重复4次调用2.1、2.2节设计的串行FIR以及LMS权值更新模块FSMO以及LMSC,为了使2个并行模块结合,以及求取误差信号,设计方案如图8所示。

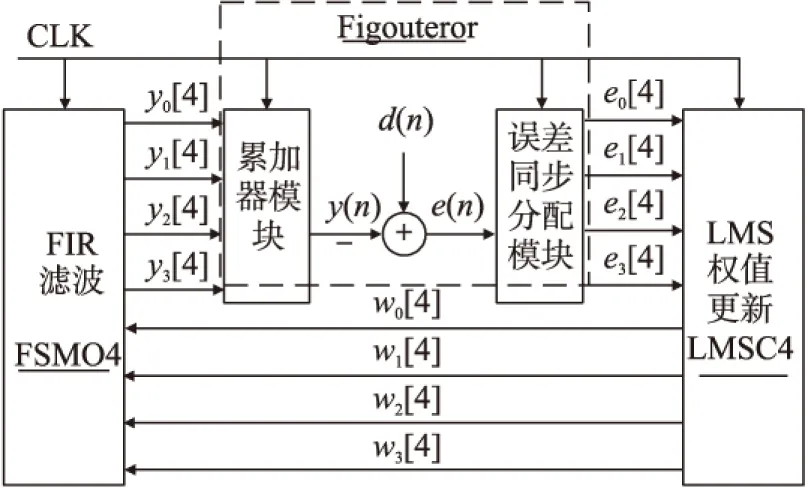
图8 求取误差信号结构图

如图8所示为求取误差信号Figouteror模块示意图,整体模块化结构的LMS自适应滤波器运行的过程中,串行模块计算出来的输出不是滤波输出,根据滤波器原理如式(4):

(4)

由于N=16故一共需要调用4个FIR串行模块,其输出分别为y0[4]、y1[4]、y2[4]、y3[4],则最终输出如式(5):y(n)=WH(n)X(n)=y0[4]+y1[4]+y2[4]+y3[4]

(5)

由于LMS算法具有严格时间顺序要求,通过图8中各模块内部对clk时钟的调用时序控制各模块计算的先后顺序。时序确定需要严格按照上述公式的顺序,设计好的模块RTL程序视图如图9所示。

由图9可知整体模块输入12为字长由X接口输入原始信号,Din输入参考信号,整体模块的输入数据输入分配采用十六位并行分配模式,并在Xap模块中调用FIFO先入先出核,每当十六位数据满时,将两组数据同步并行输出到LMS自适应滤波器模块中,分别由并行调用的4组LMSC模块更新权值以及FSMO滤波模块滤波,滤波输出以串行方式从Y接口输出。

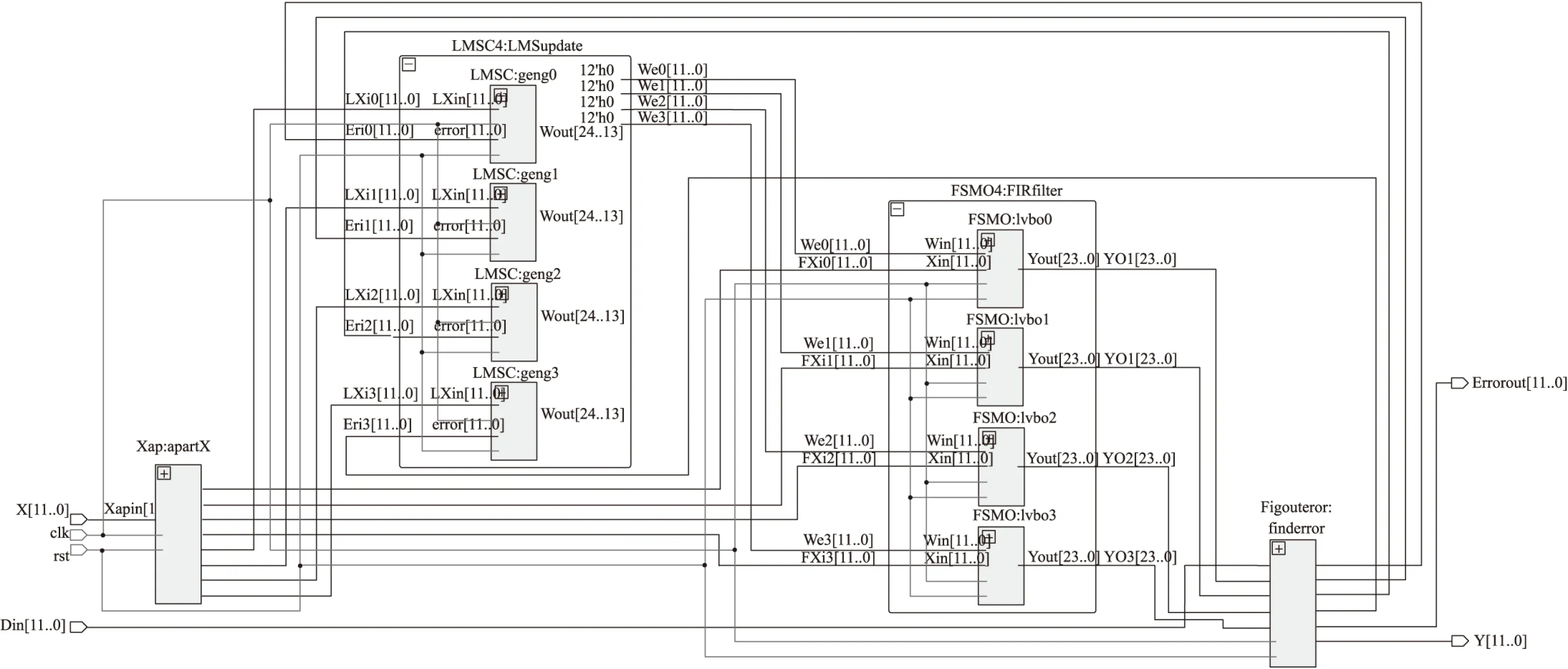
图9 整体模块化LMS自适应滤波器设计的RTL视图

利用上述原理,分别设计32阶以及64阶的LMS自适应横向滤波器,并对其调用逻辑资源以及数据处理速率进行比较。

3 实验结果及分析

整体结构设计完整之后进行RTL级程序编程,调用芯片乘法器资源,对整个系统进行设计,使用3种设计方法设计参数为15阶(N=16)与31阶(N=32)的自适应滤波器,一种是全串行结构,以及全并行结构,还有本文所述的模块化设计方法,模块化1调用4组并行模块,模块化2调用8组并行模块,并设计阶数N=64的63阶滤波器,此时全并行设计由于过于消耗乘法器资源所以没有设计的意义,故调用16组串行模块进行模块化设计,为了便于对比,采用统一的系统时钟约束条件为10ns,目标器件采用Altera公司的cycloneIV系列芯片EP4CE15F17C8,调用逻辑资源以及数据处理速率比较如表1所示。

根据表1、表2绘制资源占用以及数据速率对比图,以串行模式结构的资源占用以及数据处理速率为基准,求取比值图如图10所示。

表1 N=16时3种结构系统资源占用以及数据速率对比

表2 N=32时3种结构系统资源占用以及数据速率对比

N=64时3种结构系统资源占用以及数据速率对比

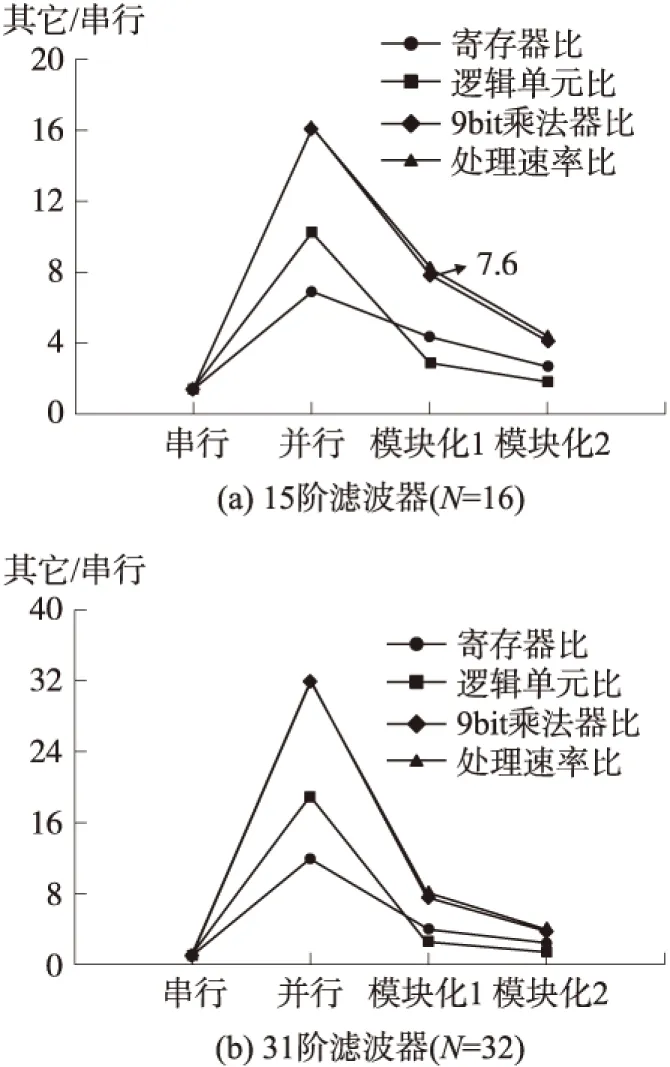
图10 设计方式对比图(与串行模式的比值)

由表格数据以及图10结果说明,模块化设计方法便于灵活利用硬件逻辑资源以及提高数据处理速率,图10(a)、10(b)中,可知全并行模式虽然处理速度能达到比较高的倍数,但是所消耗的寄存器以及逻辑单元都是所有结构中最高的,而模块化设计的LMS自适应滤波器通过并行调用基本模块模块化1设计结构调用了8组串行模块,达到了近7.6倍的数据处理速度。并且在较高阶数N=32与N=64时均能达到较好的提升速度的效果,在设计N=64的自适应滤波器时,全并行结构必须使用128个硬件乘法器资源,很多FPGA芯片乘法器资源都不足以满足要求,采用软件乘法则会大大制约数据处理速率,此时采用模块化设计的灵活性就凸显出来。所以,采用模块化设计,满足FPGA设计LMS自适应滤波器的结构灵活性,更加利于FPGA设计时资源与处理速率的灵活选择。

4 结论

本文首先介绍了LMS自适应算法的基本原理,然后分别介绍了FIR串行模块以及LMS串行模块的设计方法,并介绍了模块的调用组合方法,编写了Verilog HDL代码,在Quartus Ⅱ 13.1中进行仿真测试。最后使用Altera公司的Cyclone IV系列的EP4CE15F17C8芯片进行了硬件测试。结果表明,采用模块化设计满足LMS自适应横向滤波器的要求,并且能提高对数据处理速度与芯片资源调用进行最优化设计的灵活性。提出的模块化LMS自适应横向滤波器设计思路也可以应用到类似的FPGA功能模块设计中。

[1] 郝天琪,崔建利,李策,等. 基于FPGA的侵彻过程数据采集系统设计[J]. 电子器件,2016,29(1):160-163.

[2] 常高嘉,冯全源. 基于FPGA的高速数据采集系统的设计与实现[J]. 电子器件,2013,35(5):615-618.

[3] 高金定. 一种改进的延迟型LMS自适应滤波器及其FPGA实现[J]. 核电子学与探测技术,2013,32(12):1450-1453.

[4] Priya D,Saravanan V,Santhiyakumari N. Power Efficient Implementation of Least Mean Square Algorithm Based Fir Filter Design Using FPGA[J]. i-Manager’s Journal on Digital Signal Processing,2014,2(1):14-21.

[5] 彭继慎,刘爽,安丽. 低信噪比下基于新型变步长LMS的自适应滤波算法[J]. 传感技术学报,2013,26(8):1116-1120.

[6] Prakash S,Kumar T G R,Raja S,et al. Active Vibration Control of a Full Scale Aircraft Wing Using a Reconfigurable Controller[J]. Journal of Sound and Vibration,2016,361:32-49.

[7] Kumar R,Bali A. FPGA Implementation of Variable Step Size Adaptive Filters for Signal De-Noising[J]. Journal of Semiconductor Devices and Circuits,2015,1(2):7-19.

[8] 张颖,李彬,赵广宇,等. 金属塑性材料细观损伤过程声发射特性实验研究[J]. 中国测试,2015,41(1):115-119.

[9] 邱陈辉,李锋,徐祖强. 基于 FPGA 和符号 LMS 算法的自适应滤波器设计[J]. 电子器件,2014,37(5):904-907.

[10] Montazerolghaem M A,Moosazadeh T,Yavari M. A Predetermined LMS Digital Background Calibration Technique for Pipelined ADCs[J]. IEEE Transactions on Circuits and Systems Ⅱ:Express Briefs,2015,62(9):841-845.

[11] 付学志,刘忠,胡生亮,等. 基于FPGA的改进型最小均方自适应时延估计器[J]. 系统工程与电子技术,2011,33(5):1191-1196.

[12] Widrow B,Hoff M E,Jr. Adaptive Switching Circuits[J]. IRE WESCON Conv Rec,1960,4:96-104.

[13] 杜勇. 数字滤波器的MATLAB与FPGA实现[M]. 北京:电子工业出版社,2015:220-252.

A Modular Design of LMS Adaptive Filter Based on FPGA*

LEIYu1,JINBaoquan1*,WANGYuncai1,ANGuangxia2,WANGYu1,WANGDong1

(1.Key Lab of Advanced Transducers and Intelligent Control System of Ministry of Education,Tai Yuan Universityof Technology,Taiyuan 030024,China; 2.Shanxi CBM(NG)Gathering and Transportation CO. LTD,Taiyuan 030032,China)

A modular design method is proposed to achieve flexibility in structure on FPGA for the LMS adaptive filter. Modular is designed conducted according to the structural characteristics of LMS algorithm and in combination with the FPGA hardware language features. It expounds the design structure of each module individually,parallel calls and integrates the modules. Comparison of the occupied resources and process rate among adaptive filters of modular design,adaptive filters of single serial design and adaptive filters of single parallel design shows that structure of 8 parallel module is nearly 7.6 times faster in process rate than that of the single serial structure,its occupied hardware resource decreases by nearly 50% than that of single parallel structure;the results show that the modular design method of LMS adaptive filter is more flexible in structure.

adaptive filter;modular design;Least Mean Square;FPGA