一种新型双腔隔振器动力学特性仿真与试验研究

周俊辉，陈前，李方硕

（南京航空航天大学机械结构力学及控制国家重点实验室，南京210016）

一种新型双腔隔振器动力学特性仿真与试验研究

周俊辉1，陈前2，李方硕3

（南京航空航天大学机械结构力学及控制国家重点实验室，南京210016）

双腔液固混合介质（SALiM）隔振器是一种适用于低频重载隔振的新型隔振器，它由主腔室、附加腔室、连通管道以及油液和波纹管弹性单元体组成的液固混合介质构成。根据连通管道中流体运动的动量方程建立隔振器非线性动力学模型，将非线性流体阻尼线性化，得出系统的等效刚度和阻尼表达式。理论分析和仿真结果表明，系统的等效刚度和阻尼具有复杂变化特性。连通管道内部油液流动受到流体阻尼力、管道内部液柱惯性力的综合影响，系统等效刚度可能会出现渐软、渐硬、振荡等复杂特性。运用MTS试验机测试隔振器在简谐位移激励下的刚度和阻尼特性，并搭建隔振试验系统。试验结果较好地验证了理论分析和仿真计算所得结论，为下一步的工程设计奠定了基础。

振动与波；液固混合介质；双腔；隔振；非线性

被动隔振装置如橡胶隔振器和钢丝绳隔振器，因其结构简单，性能可靠而在工程中得到广泛应用。尽管工程中已经应用多种类型的隔振器[1–3]，但是依然迫切需要研究和开发新的隔振器，以应对机械设备越来越严苛的工作环境，以及满足人们对固定结构、交通工具等舒适性的更高要求[4]。SALiM隔振器是一种适用于重载机械低频隔振的新型隔振装置。最新式的SALiM隔振器采用波纹管容器作为可变形压力容器，以波纹管单元体作为弹性介质，具有诸多优良特性[5]。波纹管结构由铝合金材料锻压而成，因而具有耐油、耐高温、抗腐蚀和疲劳寿命长等优点，使SALiM隔振器具有更加稳定的隔振性能。由于容器的端部通过焊接密封，解决了可能存在的油液泄漏问题，而空气弹簧很难杜绝慢漏气的问题。此外，可以通过填充不同数量的弹性单元体来改变SALiM隔振器的刚度特性。

在单腔室SALiM隔振器的基础上做改进，设计一种带附加腔室的SALiM隔振器。主、附加腔室通过连通管道连接，系统振动时会驱动油液在连通管道中来回流动，从而会消耗大量能量。附加腔室作为弹性元件和原本的隔振器串联布置，因而可以进一步改善系统的刚度特性。以双腔空气弹簧为代表的双腔隔振系统在隔振领域获得了广泛的运用[6–7]。借鉴双腔空气弹簧的相关理论，建立双腔SALiM隔振器的复刚度模型，得到了系统等效刚度和阻尼的表达式。与双腔空气弹簧不同，在分析双腔SALiM隔振系统连通管道两端的压差流量特性时必须考虑油液的惯性力。而油液振动对于系统动力学特性的影响是研究重点之一。另一个重点是考察节流开度对于系统动力学特性的影响。文章第一部分介绍了双腔隔振系统的动力学模型；第二部分通过理论和数值仿真分析了系统刚度阻尼的变化特性；第三部分给出了刚度、阻尼特性试验测试结果。

1 隔振器结构及动力学模型

图1为双腔SALiM隔振器物理模型，隔振器包括主腔室、附加腔室以及连通管道三个主要部分，其中两个腔室内部充满油液和弹性单元体组成的混合介质。

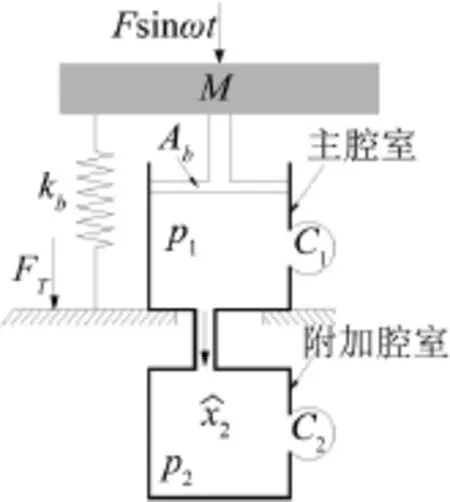
图1 隔振器的等效物理模型

主腔为可压缩的多层波纹管容器，既是压力容器也是承力构件，其自身的刚度和等效截面积分别为kb和Ab，内部油压和单元体集合的体积柔度分别为p1和C1。附加腔室为刚性容器，其内部油压和单元体集合的体积柔度分别为p2和C2。连通管道的长度、直径及截面积分别为li、di和Ai，连通管道上安装了节流阀，节流阀的流通面积为Av，其大小受节流阀开度控制。假设隔振器受到f=Fsinωt的简谐激励力作用，载荷质量M位移响应为x1，流体相对于管道的位移为x2，隔振器传递至基础的力为FT。

根据连通管道内油液运动的动量方程可以得到[8]

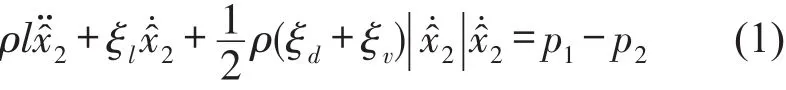
式中ξl表示流体流经连通管道的损耗因子，其值为表示流体的动力粘度，ξd表示流体进出管道时截面突变引起的局部损耗因子表示流体流经阀口的损耗因子，Cd表示流量系数，当AiAv＞49时，流体完全收缩，取Cd=0.61～0.62，不完全收缩时，Cd=0.7～0.8。

由于工作压强较低，忽略油液的可压缩性，则图（1）中主腔活塞扫过的体积等于两腔室内单元体的体积压缩量，流经连通管道的油液体积等于附加腔室内单元体的体积压缩量，故有

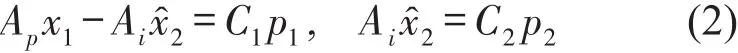
载荷质量受到激励力、主腔波纹管弹性力和主腔油压力的共同作用，其运动方程及隔振器传递至基础的力分别为

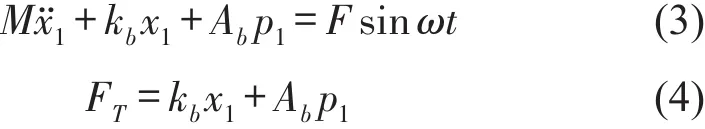
图2为隔振器的等效力学模型，其中mi表示连通管道中液柱的等效质量，液柱的等效质量相比其真实质量放大了R2倍，因此振动过程中液柱作用被放大了。

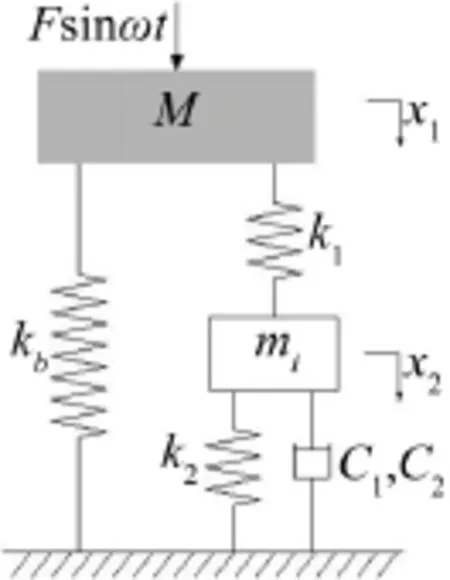
图2 隔振器等效力学模型

2 隔振器的刚度和阻尼特性

2.1 简化后的等效刚度和阻尼模型

假设系统在简谐激励作用下，位移响应x1和x2做简谐运动，其位移形式如下

X1与X2表示x1和x2的振动幅值，θ表示x2与

2.2 等效刚度和阻尼的理论与数值仿真研究

定义k0=k|ω→0和k∞=k|ω→∞，基于式（13）可以得到k0和k 的值分别为

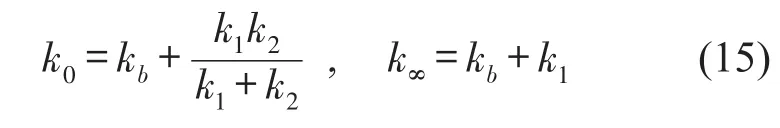
由式（6）分析可得连通管道中液柱的共振频率为

当ω=ωn时，将其代入式（13），得到液柱共振时的等效刚度值为

可以看出这三个点(0，k0)，(fn，k∞)，(+∞，k∞)是与外激励和系统阻尼参数无关的定点，这一性质可用来识别系统的刚度参数。

对式（13）求导并令其导数等于零，得到等效刚度取极值时的频率ω1和ω2，进一步求导分析发现等效刚度在ω=ω1处取得最小值，在ω=ω2处取得最大值，将其代回式（13），可以得到等效刚度的最小值kmin和最大值kmax，定义液柱振动方程的等效阻尼比为ξ，则

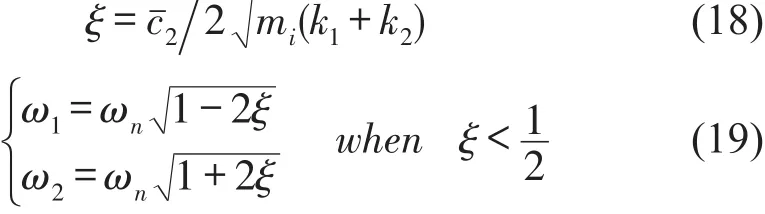
因此，当ξ＜1 2，ω∈(0,ω1)⋃(ω2,+∞)时，系统的等效刚度随频率的增大而减小，当ω∈(ω1,ω2)时，系统的等效刚度随频率的增大而增大；等效刚度的最小值随ξ的增大而增大，最大值随ξ的增大而减小，表明增大流体阻尼能够抑制液注共振的影响。

对式（14）求导，类似可得到等效阻尼最大值cmax及其对应频率ω3为

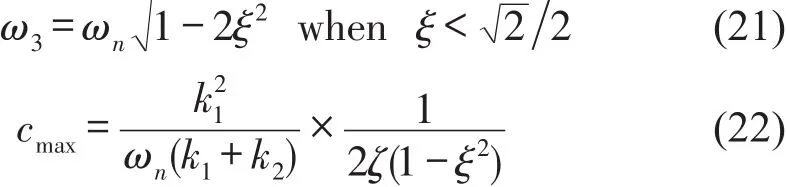
由式（21）可知，当ξ＜2 2时，随ξ增大，峰值频率左移，对式（22）分析可得，当ξ∈(0,3 3)时，cmax随ξ的增大而降低，当ξ∈(3 3,2 2)时，cmax随ξ增大而增大。

这里λ、z1、z2、fe、fT分别是ω、x1、x2F、FT的无量纲化形式，当隔振器无负载情况下受到正弦位移z1激励时，基于式23(b)和式23(c)进行数值仿真，通过识别FT=k x1+cx1中的参数得到数值仿真结果，而理论结果则是基于等效刚度和阻尼表达式（13）和式（14）获得。相关的仿真参数设置为kr=2.4×105N/m，ζ1=0.95，ζb=0.1，ξ1=0.25，ξ2∈[1 ×10-2，1 ×102]，图3为无量纲化后的等效刚度和阻尼变化特性曲线，从图中可以看出数值仿真结果与理论结果基本吻合，证明了等效刚度和阻尼模型的正确性。

隔振器的连通管道上安装有节流阀，可近似认为阀门从开启到关闭过程中，平方阻尼系数c2从零到无穷大变化。从图4可以看到等效刚度曲线均相交于点(ωn、k∞)，c2较小时，等效刚度在液柱共振频率两侧出现谷值与峰值，随着c2的增大，液柱振动方程的等效阻尼比ξ增大，等效刚度的谷值增大、峰值降低，当ξ2=10时，等效刚度的谷值和峰值消失，等效刚度随着频率的增大迅速升高并趋近于k∞。

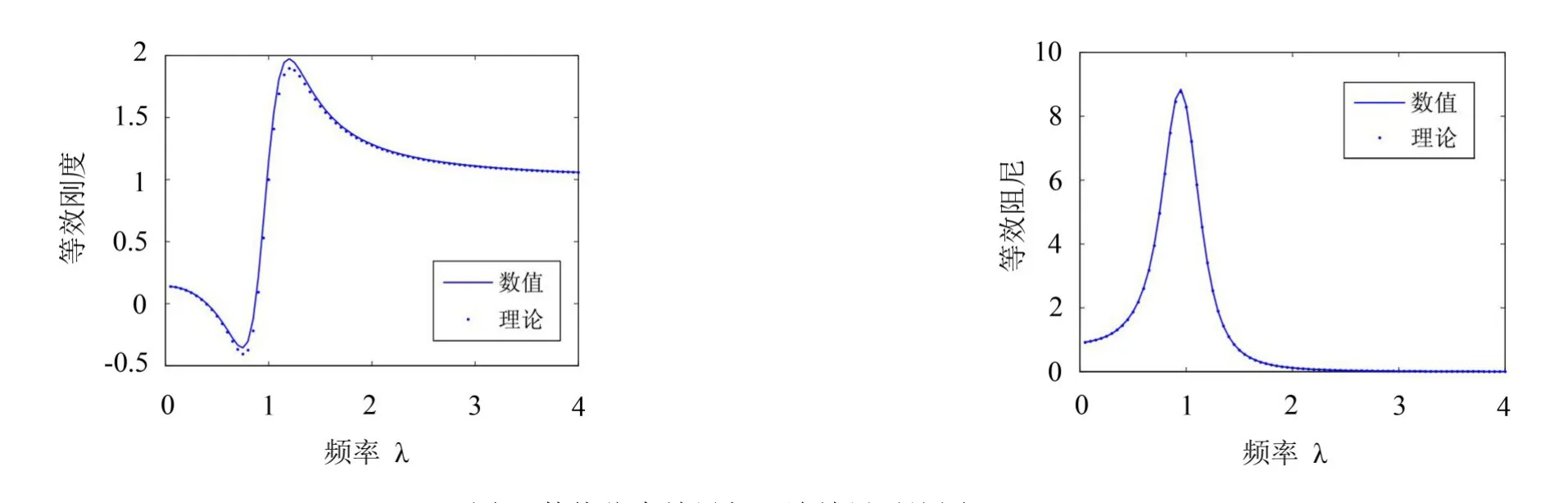
图3 数值仿真结果与理论结果对比图（ξ2=0.1）

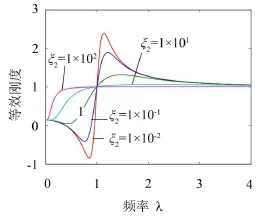
图4 非线性阻尼对等效刚度的影响

这是因为连通管道内部的流阻作用包括流体阻尼力和和液柱惯性力，小阻尼情况下液柱惯性力起主导作用，具体表现为低频段等效刚度值下降，在液柱共振处出现急剧变化；大阻尼情况下流体阻尼力起主导作用，液柱共振受到抑制，等效刚度值迅速增大。

从图5可以看出c2较小情况下，等效阻尼在液柱共振频率附近取得峰值，随着c2的增大，峰值阻尼和对应的频率均减小，c2超过某个值之后，等效阻尼的峰值随c2的增大而增大，这与等效阻尼理论的分析结论是一致的。

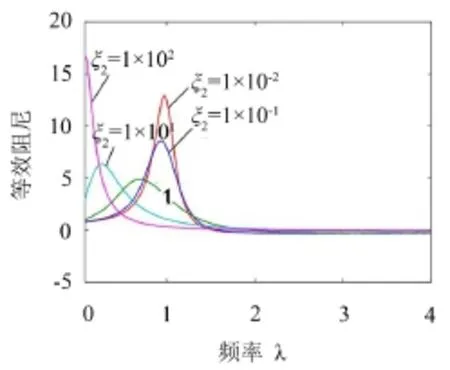
图5 非线性阻尼对等效阻尼的影响

因为双腔SALiM隔振器的等效阻尼取决于两个因素，一是管道阻尼水平，二是液柱振动的响应水平，后者受前者的制约，而液柱的响应水平随频率的升高而衰减，这是等效阻尼呈现复杂变化特性的原因，当流体阻尼很大时，可以忽略液柱振动的影响，等效阻尼峰值消失。

3 动态特性试验

为了验证理论的正确性，利用疲劳试验机对隔振器进行动态特性实验，图6中疲劳试验机夹头夹持的波纹管容器为主腔室，左侧油缸为附加腔室，两腔室通过油管连接，油管中间安装有高压球阀。用β表示球阀的开度，β=0表示阀门全开，β≥60表示阀门关闭。通过疲劳试验机上夹头对主腔室进行正弦位移激励，由于受限于疲劳试验机性能影响，试验的频率范围选择在0～20 Hz之间。

图6 隔振器动力学特性实验

双腔SALiM隔振器可通过改变阀门开度来调节连通管道的阻尼参数，平方阻尼系数c2随β的增大而增大，当β≥60时，阀门关闭时，c2取无穷大。图7中箭头表示β增大的方向，随着β的增大等效刚度的谷值增大，峰值减小，这是因为增大阻尼抑制了液柱共振的影响，这与式（20）分析得出的结论是一致的，当β=57时，等效刚度近似有keq=k∞。不同阀门开度下的等效刚度曲线均在频率点f=8Hz处相交，从而证明了定点(ωn，k∞)的存在。

图7 阀门开度对等效刚度的影响

从图8中等效阻尼曲线可以看出，阀门开度较大情况下，c2较小，等效阻尼峰值频率ω3与液柱共振频率ωn接近，随着阀门开度减小，ω3向坐标轴原点方向移动，继续减小至某一开度之后，等效阻尼峰值消失。

图8阀门开度对等效阻尼的影响

图7和图8反映的等效刚度和阻尼的变化规律与图4与图5仿真曲线变化趋势基本一致，说明理论建模的准确性。

4 结语

通过理论分析、数值仿真和试验验证相结合的方法对于双腔隔振系统的刚度阻尼特性进行较为详细的讨论。对于连通管道内部的油液运动，当流体阻尼力起主导作用时，系统主要表现为刚度渐硬特性，且刚度增长速度随着节流开度的减小而增大；而当液柱惯性力起主导作用时，系统刚度在液柱共振点附近出现振荡现象，且振荡幅度随着节流开度的减小而减小。隔振器的等效阻尼和流体阻尼系数以及液柱振动水平有正相关关系，当外激励一定时，液柱振动水平随着流体阻尼系数增大而减小，因而无法简单地通过调节阀门开度改善系统的耗散特性。有关结论为双腔SALiM隔振器的进一步改进设计提供了参照，也是下一步进行主动节流控制工作的基础。

[1]PLOOY N D,HEYNS P S,BRENNAN M J.The development of a tunable vibration absorbing isolator[J]. International Journal of Mechanical Sciences,2005,47 (7):983-997.

[2]WINTERFLOOD J,BLAIR D G,SLAGMOLEN B.High performance vibration isolation using springs in Euler column buckling mode[J].Physics Letters A,2002,300 (2-3):122-130.

[3]YILMAZ C,KIKUCHI N.Analysis and design of passive band-stop filter-type vibration isolators for low-frequency applications[J].Journal of Sound&Vibration,2006,291 (3-5):1004-1028.

[4]朱石坚.振动理论与隔振技术[M].北京：国防工业出版社，2006.

[5]GAO X,CHEN Q,TENG H D.Modelling and dynamic properties of a novel solid and liquid mixture vibration isolator[J].Journal of Sound&Vibration,2012,331 (16):3695-3709.

[6]LEE J H,KIM K J.Modeling of nonlinear complex stiffness of dual-chamber pneumatic spring for precision vibration isolations[J].Journal of Sound&Vibration, 2007,301(3-5):909-926.

[7]FAN R,LU Z.Fixed points on the nonlinear dynamic properties of hydraulic engine mounts and parameter identification method:Experiment and theory[J].Journal of Sound&Vibration,2007,305(4-5):703-727.

[8]游有彭.液压与气压传动[M].北京：科学出版社，2008.

Simulation and Experimental Research on Dynamics Characteristics of a Novel Dual-chamber Isolator

ZHOU Jun-hui,CHENQian,LI Fang-shuo
（State Key Laboratory of Mechanics and Control of Mechnical Structures, Nanjing University ofAeronautics andAstronautics,Nanjing 210016,China）

The dual-chamber Solid and Liquid Mixture(SALiM)isolator is a novel isolator which is designed for vibration isolation of heavy equipment with low frequency.It consists of main chamber,additional chamber and the oil pipe connecting the two chambers.According to the momentum equation of the fluid in the connection pipe,the nonlinear dynamic model of the vibration isolator is established.The equivalent stiffness and damping expressions are derived by simplifying the nonlinear fluid damping to a linear viscous damping when the isolator is excited by harmonic signals.The theoretical and simulation results show that the equivalent stiffness and damping of the system have complex properties. Since the internal flow of the connection pipe is affected by the fluid damping force and the inertia force of the liquid column in the pipe,the isolator may show stiffness hardening or softening effects under various situations.The stiffness and damping characteristics of the isolator are tested by an MTS.A vibration isolation system is established to test the frequency response characteristics of the isolator.The experimental results verify the theoretical and simulation results.This work provides a foundation for the engineering design of the isolators.

vibration and wave;solid and liquid mixture;dual-chamber;vibration isolation;non-linearity

A

10.3969/j.issn.1006-1355.2017.02.035

1006-1355(2017)02-0173-05

2016-11-01

周俊辉（1990－），男，湖南省永州市人，硕士生，主要研究方向为减振与振动控制。E-mail:jhzhou_detec@nuaa.edu.cn

陈前，男，博士生导师。E-mail:q.chen@nuaa.edu.cn