不同边界条件下由阻尼材料所制振动梁仿真计算

郝敏，苏正涛，裴高林，王辰，陈高升,张浩

（中国航空发动机集团公司北京航空材料研究院，

减振降噪材料及应用技术航空科技重点实验室，北京100095）

不同边界条件下由阻尼材料所制振动梁仿真计算

郝敏，苏正涛，裴高林，王辰，陈高升,张浩

（中国航空发动机集团公司北京航空材料研究院，

减振降噪材料及应用技术航空科技重点实验室，北京100095）

根据不同边界条件下振动梁的模态测试结果确定了振动梁振型和材料损耗因子，再由谐响应计算得到振动梁激励点和端点峰值、材料损耗因子，比较两种结果的差异，最终发现振动梁试样一端连接激振设备、另一端无约束（为自由端）、水平放置的实验方案最为合理。同时针对单个振动梁试样在测试频段内共振数据少的缺陷，采用改变试样长度、测试多组试样的方法加以规避。

振动与波；振动梁；边界条件；模态振型；损耗因子；仿真计算

材料阻尼性能的测试方法有:对数衰减法、共振放大法和半功率带宽法[1–3]。

对数衰减法相对简单，对可以简化为单自由度的系统比较适用。共振放大法的实测系统等效静位移无论是从加载设备和采集设备上都有一定的困难，难以实施。工程上常用半功率带宽法对结构的阻尼性能进行测试，半功率带宽法简便易行且精度能够满足大多数工程需求，故这种方法得到了广泛的应用[4]。

测试参考GB/T 18258-2000《阻尼材料阻尼性能测试方法》的相关规定进行，该方法的实质为半功率带宽法。该标准规定的测试频率范围为50 Hz～5 000 Hz，分析频率范围为1 000 Hz～5 000Hz，满足标准规定的测试要求。按照标准规定构建振动梁测试系统，测试系统的仪器由激励和检测两部分组成。由信号发生器产生一个正弦或随机信号，经放大器、激励激振器，对试样施加激振力。由检测传感器检测试样的振动响应信号，经放大器放大后送入显示与记录仪器，保持激振幅值恒定，连续改变频率测出试样的共振曲线，根据所测共振频率和半功率带宽，依据所给公式可计算出材料的各模量值和损耗因子[5]。

1 实验及计算

1.1 试样

被测试样为振动梁，振动梁是由金属层和阻尼层构成的复合试样，其结构示意图见图1。

图1 振动梁试样示意图

阻尼材料阻尼性能测试方法中推荐使用的振动梁宽度为10 mm，试样自由端长度为180 mm～250 mm，厚度为1 mm～3 mm。试验时选择振动梁长为220 mm，宽为10 mm，其中H＞H1，H为1 mm，H1为0.3 mm，基梁总厚度为2.3 mm。整个基梁L采用金属铝，L1段为实心金属铝，L2段中间夹有阻尼材料。阻尼材料为丁基橡胶类，其弹性模量约为8.7 MPa。

1.2 材料阻尼实验方案设计

参考GB/T18258-2000《阻尼材料阻尼性能测试方法》中的测试方法，文中提出了3种测试方案。方案1如图2所示，被测试样一端刚性固定在试验支架上部，另一端连接激振设备，激振设备的底座刚性固定在试验支架下部，试验支架底部固定在刚性基础上。

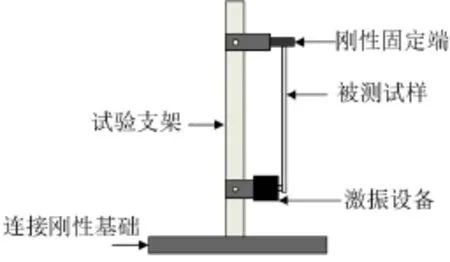
图2 方案1试验示意图

方案2如图3所示，被测试样一端无约束（自由端），另一端连接激振设备，激振设备的底座刚性固定在试验支架上部，试验支架底部固定在刚性基础上。方案3如图4所示，被测试样一端连接激振设备，另一端无约束（自由端），水平放置，激振设备底部固定在刚性基础。

图3 方案2试验示意图

图4 方案3试验示意图

1.3 不同实验方案的仿真计算

针对三种方案的特点建立三种方案的有限元模型（建模时输入已知的阻尼材料损耗因子），采用谐响应分析的方法模拟正弦扫频试验以求得被测试样的加速度振动响应曲线，根据GB/T18258-2000《阻尼材料阻尼性能测试方法》中的方法结合上述得到的被测试样的加速度振动响应曲线，求得阻尼材料的损耗因子，并将其与已知的材料损耗因子进行比较，对比不同方案的优劣。

图5 振动梁前6阶模态振型

采用Ansys16.0 workbench的mesh模块对方案3的几何模型进行网格划分，采用结构化六面体网格，控制网格的最小尺寸为1 mm。计算得到振动梁前6阶模态振型见图5。

按照试验方法测试出的共振频率所对应的振型主要集中在长度方向及厚度方向所确定平面内的弯曲振动。结合仿真计算结果，振动梁试验时能够测出的共振频率及其对应的振型为表1中的1、4、5阶共振。

表1 方案3振动梁模态计算结果

1.4 谐响应计算

当谐响应分析的频段设置较宽，并提供单位激励力时，其相当于进行一次扫频试验，从而能够求得结构在白噪声作用下的频率响应函数，而根据GB/T 18258-2000《阻尼材料阻尼性能测试方法》中的试验方法，其实质即为求解振动梁的频率响应函数，之后确定阻尼材料的损耗因子，因此利用谐响应分析对该试验进行仿真模拟是最为合适的。

动力学运动方程为

式中

[M]——结构质量矩阵；

[C]——结构阻尼矩阵；

[K]——结构刚度矩阵。

对于谐响应分析而言力矩阵{F(t)}和位移矩阵{u}是简谐的，频率为ω，力矩阵和位移矩阵以复数形式表示为

式中

Fmax为力的幅值；

φ为力函数的相位角；

F1=Fmaxcosφ，为力的实部；

F2=Fmaxsinφ，为力的虚部；

umax为位移的幅值；

ϕ为位移函数的相位角；

F1=Fmaxcosφ，为位移的实部；

F2=Fmaxsinφ，为位移的虚部。

因此谐响应分析的运动方程为

计算时在激励点施加1 N的激励力，激励频率范围为1 000 Hz～5 000 Hz，利用模态叠加的方法对振动测试点的振动响应进行计算，图6和图7分别为振动梁激励点及端点的响应曲线，其中粗线为响应幅值标准化曲线，细线为响应相位角标准化曲线。从图中可以看出在1 000 Hz～5 000 Hz频段范围内出现2阶共振峰值，分别对应模态计算时的1 763.4 Hz（XY平面3阶弯曲）及4 073.3 Hz（XY平面5阶弯曲），而模态计算时的2 781.6 Hz（XY平面4阶弯曲）未出现相应峰值，这是由于该频率所对应的模态振型在激振点出现了节点（振型位移为0的点），无法将该振型激出。

图6 振动梁激励点振动响应曲线

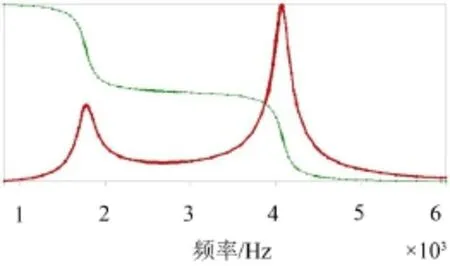
图7 振动梁端点振动响应曲线

当利用谐响应分析求解出振动梁的振动响应曲线后就可以利用GB/T 18258-2000《阻尼材料阻尼性能测试方法》推荐的计算方法对阻尼材料的损耗因子进行计算，计算公式如下

式中G为阻尼材料弹性剪切模量，Pa；

η2为阻尼材料剪切损耗因子，无量纲；

ηsi为复合板的损耗因子，无量纲；

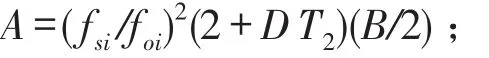
fsi为复合板第i阶共振频率，Hz；

foi为金属板第i阶共振频率，Hz；

D为阻尼材料密度和金属材料密度之比，无量纲；

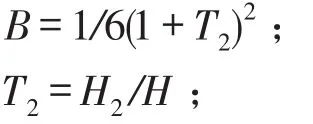
H为振动方向板体厚度，m；

H2为阻尼材料厚度，m；

Ci为第i阶模态系数，其中

Ci=(π/2)(i-0.5)（i＞3时）；

i为共振阶数(i=1，2，3，…)

ρ为板体密度，kg/m3；

l为板体长度，m。

由以上各式知道，测得振动梁试样有关数据和各阶共振频率以及结构损耗因子，就可以求出阻尼材料本身的弹性模量和损耗因子。

从表2计算结果可以看出，进行谐响应分析时，由于阻尼因素的影响，振动梁的响应峰值与模态计算结果略有偏差，这主要是由于数值计算误差所引起，同时从损耗因子的计算误差可以看出，振动梁端点（自由端）的计算误差比振动梁激励点的计算误差小，同时随着分析频段的上升损耗因子的计算误差逐渐减小。

采用同样的方法对方案1进行模态试验及谐响应计算，在方案1中出现的其他共振峰值实际上为伪数据，由于这些伪数据引入了夹具的影响，其不能利用上述标准中的计算公式进行损耗因子计算。但是在试验条件下无法判断哪些是伪数据，哪些是真实数据，故采用方案1的设计方法进行材料阻尼试验测试是不合适的。同时由于要求的分析频段较高，若想夹具的共振频率完全避开分析频段，一方面需要将夹具设计得较软，使频率低于1 000 Hz下限，或者将夹具设计得刚性较强，使其高于5 000 Hz上限，对于前者就失去了该方案夹具一端固定的意义，而对于后者实现的难度非常大，经济代价也比较高。最后对比方案3的简单易行且数据准确的特性，不推荐利用方案1的方法对材料的内损耗因子进行测试。

比较方案2与方案3可以确定，由于在方案2中试样一端与激振器直接连接，而另一端处于自由状态，根据激振器的原理，激振器与试验试样是通过“激振杆+弹簧”连接的，即相当于激振器与试样弹性连接，因此方案2中的试验夹具的共振频率一般不会对试样造成影响，其效果相当于试验方案3。

1.5 试样设计

在其他参数不变的情况下，通过改变振动梁长度的方法加工不同的试样，采用方案3对其进行模态分析以确定不同试样在1 000 Hz～5 000 Hz频段范围内的共振点。其中试样的长度在180 mm至250 mm间隔10 mm分别取值，通过有限元模态计算，其结果见表3和图8。

由于不同试样长度条件下的相同阶数弯曲振型都一致，仅对应频率不同，在此仅列出1 000 Hz～5 000 Hz频段范围内的出现的振动梁2～6阶弯曲频率，而不区分其对应的试样长度。

将方案3一组试样的计算频点与表3中计算得到的利用多个试样进行组合后得到的计算频点绘制图，见图9。

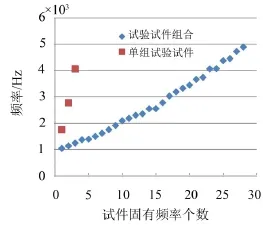
图9单组试验试样与试验试样组合对比分析

图9中x轴表示频点编号（按计算频率的从小到大），y轴表示计算频点所对应频率值（Hz）。从图中可以看出，在方案3中（单组试验试样）在1 000 Hz～5 000 Hz计算频段内，仅有3个频点的数据，而在方案3的基础上通过加工不同长度试验试样后进行组合试验可以得到28个计算频点数据，且这28个数据在分析频段内均匀分布，之后利用上文的方法对这28个计算频点的响应数据进行分析得到对应频率下的阻尼材料损耗因子，与之前的方法对比，能够解决在分析频段范围内数据不足的问题。

表2 方案3阻尼损耗因子计算结果

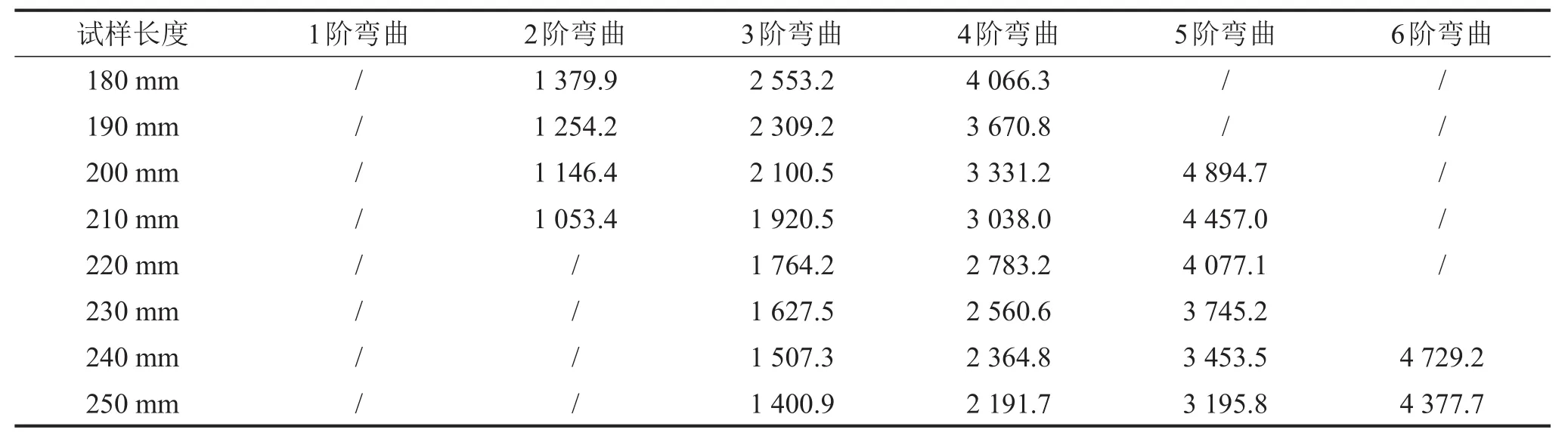
表3 不同试样模态有限元计算结果/Hz

图8 2～6阶振动梁弯曲振型

2 结语

（1）由于实施方便，数据精度满足工程要求，且试验时不受试验夹具的影响，采用方案3为最终的试验方案。方案3的振动梁试样一端连接激振设备，另一端无约束（自由端），水平放置。在试验方案3中试样的重量对阻尼材料损耗因子的计算结果不会产生大的影响。

（2）在方案3的基础上可以通过改变试样的长度来多加工几组试样以改进单个试验试样在测试频段内共振数据少的缺陷。

[1]戴德沛.阻尼减振降噪技术[M].西安：西安交通大学，2007.

[2]徐丰辰，李洪林，刘福.阻尼材料动态阻尼系数的测定[J].粘接，2013，9(3)：45-49.

[3]Garrett S L.Resonant acoustic determination of elastic moduli[J].Journal of the Acousticl Society of America, 1990,(88):210-221.

[4]陈高升.冰箱压缩机系统振动传递率预估与振动特性研究[D].西安：西安交通大学，2007.

[5]裴高林，米志安，苏正涛，等.约束阻尼材料性能测试方法的探讨[J].噪声与振动控制，2008，28(3)：156-159.

Simulation of Vibration of Beams Made of Damping Materials with Different Boundary Conditions

HAOMin,SU Zheng-tao,PEI Gao-lin,WANGChen,CHEN Gao-sheng,ZHANGHao
（Beijing Institute ofAeronautical Materials,Aviation Key Laboratory of Science and Technology on Materials andApplication Research for Vibration and Noise Reduction,Beijing 100095,China)

According to the modal testing results of vibrating beams under different boundary conditions,the modal shape and material loss factor are obtained.Through the harmonic response computation,the peak values of the responses at the excitation point and the end of the beam and the loss factor of the material are derived.Comparing these results mutually, it can be concluded that the horizontally placed beam with one end excited and the other end free is the most reasonable. Finally,due to the shortage of the resonance data in the frequency range of the test,several sets of beam specimens with different lengths are tested.

vibration and wave;vibrating beam;boundary condition;modal shape;loss factor;simulation

O327

A

10.3969/j.issn.1006-1355.2017.02.005

1006-1355(2017)02-0023-05

2016-09-30

郝敏（1984－），女，河北省保定市人，硕士，工程师，主要研究方向为特种橡胶材料和材料试验方法。E-mail:haomin_mail@163.com