基于误差四元数的火箭主动滚转控制技术研究

郑 新，杨宇和，严宝峰，付维贤，赵 民

（1. 北京宇航系统工程研究所，北京，100076；2. 中国运载火箭技术研究院，北京，100076）

基于误差四元数的火箭主动滚转控制技术研究

郑 新1，杨宇和1，严宝峰1，付维贤1，赵 民2

（1. 北京宇航系统工程研究所，北京，100076；2. 中国运载火箭技术研究院，北京，100076）

火箭助推段主动滚转飞行时，由于箭体的持续性滚转引起耦合效应，使其动力学和控制特性变得复杂。对于采用捷联惯组方案的主动滚转火箭，四元数控制方法可以不需要或减少姿态角的三角函数解算，避免欧拉角解算出现奇异值等问题。针对捷联惯组方案的助推段主动滚转火箭，对其动力学特性和误差四元数控制技术进行了相关研究。

滚转火箭；姿态控制；误差四元数；

0 引 言

火箭助推段主动滚转飞行时，箭体的持续滚转将使其运动及动力学特性呈现新特点，并对控制系统产生影响。

对于采用捷联惯组方案的主动滚转火箭，四元数控制方法可以不需要或减少姿态角的三角函数解算，避免欧拉角解算出现奇异值等问题；也便于在以姿态角偏差反馈控制的方案基础之上实现滚转飞行控制。

本文针对采用捷联惯组方案的助推段主动滚转火箭，对其动力学特性和误差四元数控制技术进行了相关研究。

1 数学模型

滚转火箭在飞行时绕箭体纵轴方向的持续自旋角运动，为便于运动与动力学特性分析和姿态控制系统设计，引入准箭体坐标系和准速度坐标系[1]，建立轴对称滚转火箭的六自由度刚体运动数学模型。

a）地面发射坐标系中的质心动力学方程，其分量形式为

式中 vx，vy，vz为箭体速度的发射坐标系中分量；x，y，z为箭体位置的发射坐标系中分量；GB′为准箭体坐标系到发射坐标系的方向余弦矩阵；GV′为准速度坐标系到发射坐标系的方向余弦矩阵。由于篇幅限制，其它符号含义参见文献[2]。

b）准箭体坐标系中的绕质心动力学方程，其分量形式为

式中Jx1′，Jy1′，Jz1′为箭体转动惯量的准箭体坐标系中分量；，，为转动惯量变化率的准箭体坐标系中分量；ωTx1′，ωTy1′，ωTz1′为箭体绝对姿态角速度的准箭体坐标系中分量；，为气动力矩偏导数的准箭体坐标系中分量；，，为控制力矩偏导数的准箭体坐标系中分量。因于篇幅限制，其它符号含义参见参考文献[2]。

由式（2）可知，由于滚转角速率ωTx1′的存在，俯仰、偏航两个通道之间存在交联项，产生了运动耦合效应，分别为气动耦合（马格努斯效应）和惯性耦合（陀螺效应）。

因火箭为轴对称式布局(Jz1′=Jy1′)，可忽略滚动通道与其他两个通道之间的交联项，认为其是独立的。

c）补充方程。包括运动学方程、控制方程、欧拉角之间的联系方程、附加方程等[2]。

d）伺服系统特性。火箭的俯仰、偏航通道多采用摆动喷管形式的推力矢量控制装置[3]，设伺服动力系统特性传递函数表示为

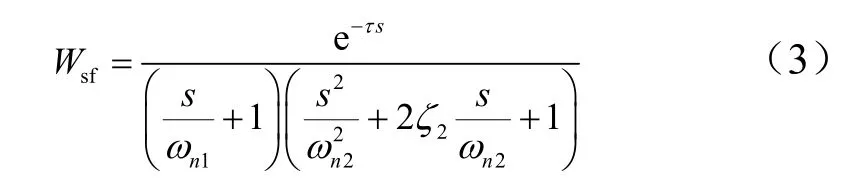
式中τ为纯延时环节的时间常数；ω1n为一阶环节的频率；ω2n，ζ2分别为二阶环节的频率和阻尼系数。

在滚转飞行条件下，伺服系统惯性等作用会产生交联耦合影响，称为控制耦合[4]。可采用双频点静态解耦法或动态解耦法对控制耦合效应在控制系统的工作频段内进行有效的对角优势化设计。

在进行控制耦合的对角优势化设计之后，为进行姿控系统的设计，还需要对其运动耦合特性进行分析，为此对运动及动力学方程进行小扰动线性化处理。

研究其小扰动运动时，系统输入量是对控制耦合处理后的俯仰、偏航通道等效舵偏角偏差Δδφ和Δδψ，输出量是俯仰偏差、偏航角偏差 Δφ和 Δψ，小扰动线性化方程的状态空间形式为

其中，

式中b1为气动阻尼力矩系数；b2为气动稳定力矩系数；b3为控制力矩系数；b4，b5为其它力矩系数；c1， c2， c3， c4， c5为相应的力系数； Δφ， Δψ为俯仰、偏航角偏差； θΔ， σΔ为弹道倾角、偏角偏差； δφΔ，Δδψ为俯仰、偏航等效舵偏角偏差。

由多变量频域控制理论[5]分析可知：在整个主动滚转飞行段，当滚转角速率ωTx1小于ωTx1_max（°）/s时，在控制系统的主要工作频段内，箭体动力学传递函数矩阵具有良好的对角优势性。姿态控制系统设计时，可忽略运动耦合效应，采用单通道控制思路进行设计。

2 滚转方案

箭体滚转方案的确定主要包括滚转飞行时段和滚转角速率的选取。

滚转飞行时段选取主要是取决于任务特性需求。

滚转角速率的选取需要从任务特性需求和火箭运动特性两方面考虑。箭体运动特性角度，主要分析耦合特性和伺服执行机构特性等因素。

取期望滚转角速率为ωTx1_exp，且ωTx1_exp小于ωTx1_max。

3 姿态控制技术

对于采用捷联惯组方案的滚转火箭，四元数控制方法可以不需要或减少姿态角的三角函数解算，既可以减轻箭上机的计算工作量，又可以避免欧拉角解算出现奇异值等问题；也便于在以姿态角偏差反馈控制的方案基础上实现滚转飞行控制。

3.1 基于误差四元数的姿控技术

本文中研究的四元数均为规范化四元数。采用误差四元数来实现火箭主动滚转控制，大致可以分为以下几步：

a）求初始姿态四元数。

根据火箭发射时的姿态来获得初始姿态四元数。姿态的欧拉角表示法比四元数表示法物理意义明确，因此，箭体的初始姿态通常以欧拉角形式给出。对于垂直发射的火箭，发射时箭体的初始姿态为

则，其四元数表达形式为

b）求当前姿态四元数。

已知初始姿态四元数时，可以利用四元数微分方程来进行姿态的实时更新解算。求解四元数微分方程的方法较多，本文采用如下的递推算法[6]，设控制系统的采样周期为h，则更新计算公式为

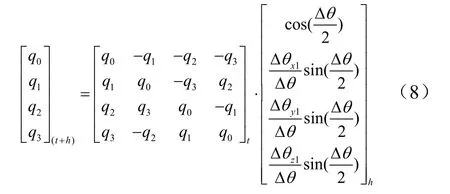
由于计算机计算精度等因素的影响，可能会导致四元数的非规范性，因此，在更新之后需要进行四元数的“规范化”处理，即令：

c）求期望姿态四元数。

求期望姿态四元数最直接的方法[7]是根据调姿目的利用当前箭体的四元数形式姿态角和角速率直接给出四元数形式的程序角。但是在传统的姿态角偏差反馈控制方案中，程序角通常是以欧拉角形式给出的，为简化实现，可直接将其转换成四元数形式，从而得到期望姿态四元数。

设欧拉程序角为φcx，ψcx和γcx，则期望姿态四元数为

d）求误差四元数。

得到当前姿态四元数和期望姿态四元数之后，便可以求得误差四元数。

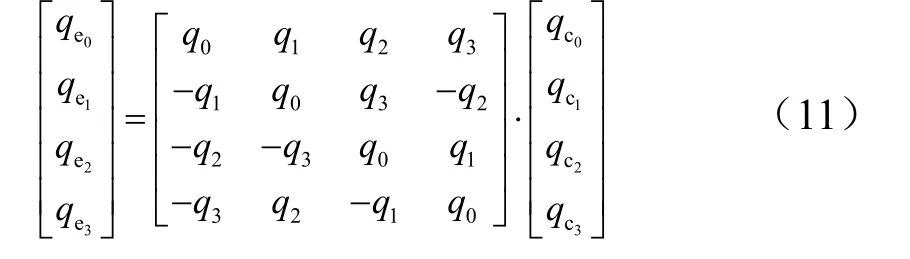
式中0eq=1。

e）求等效摆角控制指令。

火箭的当前姿态四元数为q，在任一控制周期内，将其按某一旋转顺序变换到期望四元数 qc需分别旋转Δφ，Δψ和 Δγ。在Δφ，Δψ，Δγ为小量的条件下，可由误差qe四元数计算其控制量[7]。

3.2 控制方程

在火箭进行主动滚转飞行时，俯仰和偏航通道采用摆动喷管、滚动通道采用滚控装置进行控制，3个通道的控制方程为

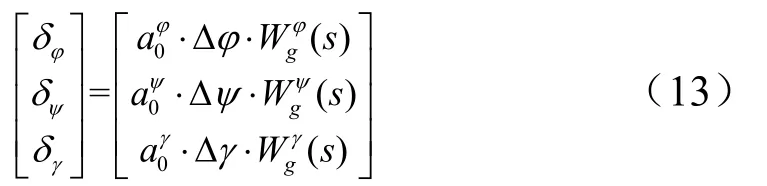
校正网络[8]取为

其中，k=φ，ψ，γ。

4 数学仿真

进行期望滚转角速率为 ωTx1_exp的六自由度数学仿真。仿真时，考虑推力矢量及滚控装置伺服系统的位置、速度和加速度限幅等特性。

在第 t0秒开始进行起旋控制，达到期望滚转角速率后保持恒定速率滚转飞行；在第t秒开始进行消旋控制，达到零滚转角速率状态后，保持零滚速状态飞行。仿真结果如图1～ 2所示。

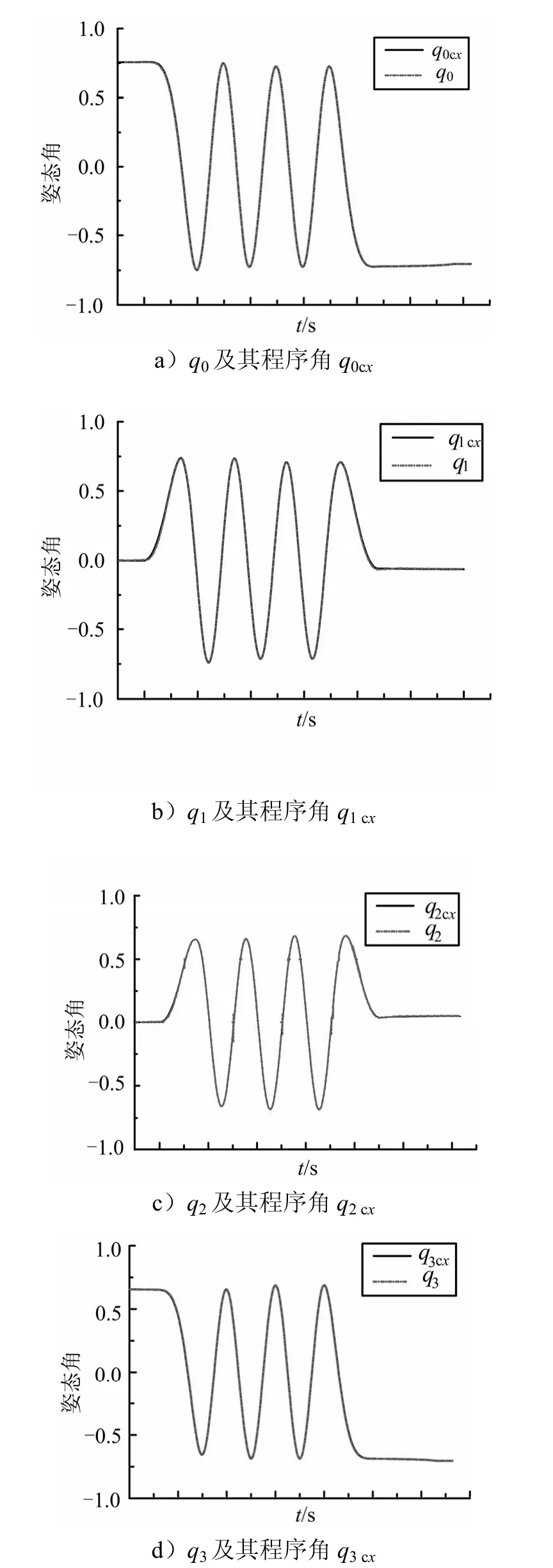
图1 四元数分量及其程序角变化

图2 姿态角速率的变化

由图1可知：姿态四元数可以实现对期望姿态四元数的精确跟随；箭体起旋后，由于持续滚转运动，尤其在箭体恒角速率滚转后，四元数的 4个分量呈现周期性变化规律。

由图2可以明显地看出起旋、恒定滚速及消旋的过程，箭体在第t1秒达到了期望滚转角速率；稳态时，角速率偏差控制在要求的姿态精度以内；由于滚控装置控制能力有限，起旋及消旋过程用时较长。

5 结 论

本文对采用捷联惯组方案的火箭助推段主动滚转控制技术进行了研究探索。研究结果表明：

a）采用误差四元数控制技术的火箭助推段主动滚转飞行技术可行；

b）应考虑提高滚控装置的控制能力，以能在较短时间内达到期望的滚转角速率。

[1]钱杏芳, 林瑞雄, 赵亚男. 导弹飞行力学[M]. 北京: 北京理工大学出版社, 2008.

[2]贾沛然, 陈克俊, 何力. 远程火箭弹道学[M]. 长沙: 国防科技大学出版社, 1993.

[3]龙乐豪. 总体设计（中）[M]. 北京: 宇航出版社, 1993.

[4]袁天保. 弹道导弹滚动飞行动力学与控制研究[D]. 长沙: 国防科学技术大学, 2005.

[5]高黛陵, 吴麒. 多变量频率域控制理论[M]. 北京: 清华大学出版社, 1998.

[6]徐延万, 余显照, 王永平, 等. 控制系统设计(上) [M]. 北京: 宇航出版社, 1991.

[7]李伶, 倪少波. 四元数反馈控制计算研究[J]. 航天控制, 2009, 27(03): 46-49.

[8]吴麒, 等. 自动控制原理[M]. 北京: 清华大学出版社, 2006.

Study on Spinning Control Technology of Rocket Based on Error Quaternion

Zheng Xin1, Yang Yu-he1, Yan Bao-feng1, Fu Wei-xian1, Zhao Min2
(1. Beijing Institute of Aerospace Systems Engineering, Beijing, 100076; 2. China Academy of Launch Vehicle Technology, Beijing, 100076)

The spinning characteristic of rocket during the boost stage will result in the coupling effect, which makes rocket’s dynamic and controlling characteristic more complex. For spinning rocket with SINS, quaternion control system can function without or with less attitude angle’s trigonometric function, thus avoiding singular values of Eulerian angle. Focusing on spinning rocket with SINS the rocket’s kinetics and error quaternions control technology are studied in this paper.

Spinning rocket; Attitude control; Error quaternion

V448.12

A

1004-7182(2017)01-0047-04

10.7654/j.issn.1004-7182.20170112

2016-05-08；

2016-08-30

郑 新（1984-），男，工程师，主要从事飞行器姿控系统总体设计及仿真