青岛市科技型中小企业融资效率研究

崔 玲 李 聪 何 帆

(青岛大学经济学院，山东 青岛 266000)

青岛市科技型中小企业融资效率研究

崔 玲 李 聪 何 帆

(青岛大学经济学院，山东 青岛 266000)

科技是第一生产力，因此为青岛市科技型中小企业选择适当的融资模式来解决其融资难题，对推动青岛市科技型中小企业的发展及青岛市经济的增长有着非常重要的意义；基于融资效率的视角，借助层次分析法与灰色关联度结合的综合模型，本文从6个不同层面对青岛市科技型中小企业的融资效率进行评价，并对青岛市科技型中小企业普遍采用的7种融资模式进行比较研究，最终得出不同融资模式与典型融资模式之间关联度的排序。

融资模式；融资效率；层次分析法；灰色关联分析

一、引言

改革开放以来，科技型中小企业在促进我国经济发展、增加劳动就业等方面发挥了关键作用。截止2015年年底，青岛市科技型中小企业年产值达到4349亿元，占2015年工业产值比重的26%。由此可见，科技型中小企业对青岛市经济发展所作出的贡献不容小觑。然而由于自身规模、融资渠道等问题，我市科技型中小企业仍然面临着融资困难这一重要难题。

为解决科技型中小企业融资难题，青岛市政府通过与社会资本及金融机构的合作，为全市科技型中小企业募得400亿元银行机构授信资金与9.9亿天使投资基金。虽然我市科技型中小企业融资难的问题在政府的帮助下得到一定程度的缓解，但仍有近75%的企业的融资需求得不到满足。而在融资过程中，影响融资效率的决定因素是融资模式的不同。因此，对我市科技型中小企业普遍选用的融资模式的融资效率的研究则显得特别重要。

二、研究回顾

对于融资理论与融资模式的研究一直是国内外当前的研究重点。Modigliani 和Miller(1958)提出了著名的MM定理，MM定理认为在特定的条件下，存在着一个最优的融资结构可以使企业价值最大化[1]；廖理和朱正芹(2003)通过对中国上市公司首次公开募股后债权与股权融资成本的实证研究，得出债权融资成本低于股权融资成本的结论[2]。

对于融资效率的研究则起步较晚。在我国，曾康霖(1993)最早提出“融资效率”这一概念，并给出了影响融资成本与融资效率的七个相关因素[3]；彭晓英(2008)利用数据包络法对已上市煤炭企业的融资效率进行了实证研究，基于研究结果提出了提高股权融资效率的方法[4]。

综上所述，国内外学者从不同角度对融资模式与融资效率进行了研究，但针对具体地市的科技型中小企业融资模式的融资效率的研究却较少。因此，本文以青岛市为例，对科技型中小企业所选取的主要融资模式的融资效率进行研究，并将互联网融资这一新型融资模式考虑进来，综合运用层次分析法与灰色关联度法对各种融资模式进行比较，以期探讨适合青岛市科技型中小企业的融资模式，进而提出解决青岛市科技型中小企业融资问题的政策建议。

三、构建融资效率评价模型

关于融资模式影响因素的相对重要性的判断，我们在专家主观意识的基础上，运用层次分析法进行研究，继而运用灰色关联法得出不同融资模式的融资效率；最后对多种融资模式的相对重要性进行排序。

(一)构造层次结构模型

对于层次分析法来说，最关键的一步是构造好的层次结构模型。对于具体评价内容来说，就是将其关键指标进行高度概括，通过科学分析将具体指标进行层层分解的过程。

在图1所构造的层次结构模型中，共包含个目标层、m个准则层和n个方案层。最终目标是得出n个方案在影响目标层的m个因素中所占的比重。

图1 层次结构模型

(二)构造判断矩阵

为了使评判结果更加合理，本文选取m名专家对融资模式的影响因素进行评判，A1,A2,…Am为与之相对应的判断矩阵。

表1 标度1-9的含义

(三)层次单排序及一致性检验

对于综合判断矩阵A*的特征值，运用归一化方法求解。在对模型归一化处理的方法选择上，本文选用和积法。步骤如下：

1、将判断矩阵A*的每一列归一化：

(1)

2、对按列归一化后的判断矩阵A*再按行相加：

(2)

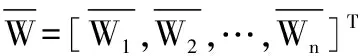
(3)

4、计算判断矩阵A*的最大特征根：

(4)

式中，(A*W)i代表向量A*W的第i个分量。

至此，我们已经求得了A*的特征值和特征向量，下一步判断矩阵A*的不一致性程度是否在容许范围内，用随机一致性比率CR表示：

CR=CI/RI

(5)

其中，CI=(λmax-n)/(n-1)，RI的值则与矩阵的阶数有关，本文中所有矩阵阶数均为6，而当矩阵阶数为6时，RI=1.26。

CR的数值反映了判断矩阵的不一致性是否在容许范围内。只有当CR≤0.1，才能说明判断矩阵的不一致性在容许范围内，能够通过一致性检验。

(四)灰色关联度分析

灰色关联度分析指的是在系统发展过程中，如果两个系统变化的态势是一致的，即同步变化程度较高，则可以认为两者关联较大；反之，则两者关联度较小。设有两个数列{Xit,Xjt}，那么两数列的灰色关联度定义如下：

(6)

其中，εij,k为t=k时{Xit,Xjt}的灰色关联系数，其计算公式为：

(7)

式中，Δij,k为t=k时刻{Xit,Xjt}之间的绝对差，即Δij,k=|Xik-Xjk|；Δmax,Δmin代表在任何时刻{Xit,Xjt}之间绝对差的最大值与最小值；ρ为分辨系数，0<ρ<1，一般取ρ=0.5。

(五)灰色关联系统的建模

设融资模式q为典型融资模式。记Xqi为典型融资模式q在第i个影响因素下所占的比重，那么典型融资模式q在所有影响因素下的比重构成特征向量为Xq={Xq1,Xq2,…，Xqn}，同时，将与典型融资模式进行关联度计算的剩余P种融资模式所构成的矩阵为：

最后，计算剩余P种融资模式与典型融资模式q之间的关联度，得到基于融资效率的不同融资模式的优先排序。

四、基于融资效率的青岛市科技型中小企业融资模式评价

本文将运用上文所构造的模型，对目前青岛市科技型中小企业普遍采用的几种融资模式进行分析研究。经过调研发现，青岛市科技型中小企业普遍采用的融资方式有内部融资、银行贷款、风险投资、民间借款、互联网金融、担保融资及财政直接融资7种融资模式，因此本文将对这7种融资模式进行展开讨论。

(一)建立层次结构模型

对于研究青岛市科技型中小企业的融资效率来说，其目标层为融资效率的评价，准则层为影响融资效率的6个因素，方案层为我们要进行评价的7种融资模式。由此可以得出图2所示的层次结构：

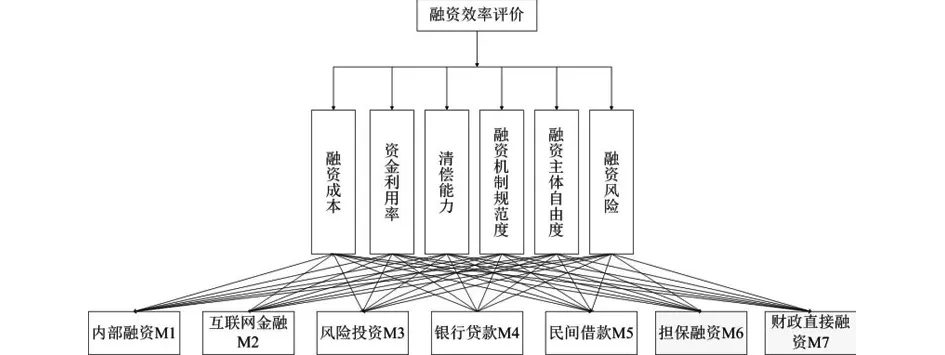
图2 融资效率评价的层次结构

(二)典型融资模式的选择及其特征向量

本文对青岛市科技局的13名专家进行问卷调查，将融资效率评价的6项影响因素之间进行两两比较，根据表一对其相对重要性进行打分，继而构建出相应的判断矩阵。在上文提到的7种融资模式中，结合已有研究成果可知内部融资的融资效率是最高的。因此，从融资效率角度，本文将内部融资看作典型融资模式，然后对其余6种融资模式的融资效率进行排序。

在本文中，我们所选取的典型融资模式为内部融资，因此可以将6个因素对目标层影响程度的比重作为内部融资的特征向量。然后利用上文所构建的灰色系统关联模型，对内部融资与其他6种融资模式的灰色关联度进行计算，便可得出基于融资效率的融资模式的有效排序。将13名专家的调查问卷的结果进行整理，每项取其平均数且保留两位小数，得出影响融资效率的6个因素的综合判断矩阵A*为：

W=[0.35，0.23，0.12，0.12，0.15，0.03]

据公式(4)可求得判断矩阵A*的最大特征根为λmax=6.1162。

最后根据公式(5)与公式(6)求得CI=0.0232，CR=0.0184≤0.1,因此综合判断矩阵A*通过一致性检验，即专家组对影响融资效率的6种因素的评价具有一致性，结果可信。

(三)确定待检验融资模式的特征向量

通过专家组对7种融资模式在影响融资效率的6个因素中进行的两两比较，构造了相应的判断矩阵，整理结果详见表2至表7(表2至表7中用字母A代表最大特征根λmax)。

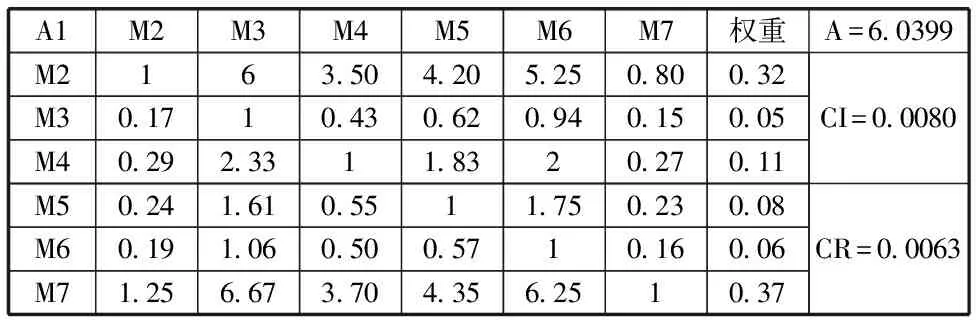
表2 融资成本下的判断矩阵及权重系数

表3 资金利用率下的判断矩阵及权重系数

表4 清偿能力下的判断矩阵及权重系数

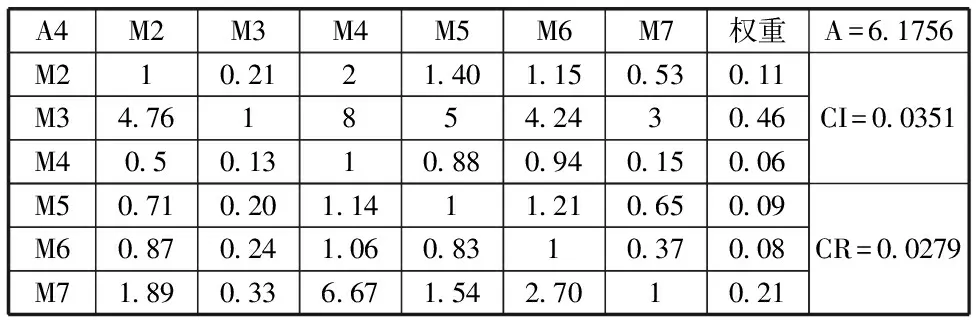
表5 融资风险下的判断矩阵及权重系数

表6 融资主体自由度下的判断矩阵及权重系数

表7 融资机制规范度下的判断矩阵及权重系数

由表2至表7的结果可知，的值均小于。因此，根据专家组的调查问卷整理得到的判断矩阵的不一致性均在容许范围之内，通过一致性检验，结果可信。于是，我们可以得到互联网金融、风险投资、银行贷款、民间借贷、担保融资及财政直接融资这6种融资模式各自的特征向量如下：

Y1=[0.32，0.24，0.19，0.11，0.27，0.20]

Y2=[0.05，0.33，0.12，0.46，0.08，0.04]

Y3=[0.11，0.20，0.21，0.06，0.08，0.39]

Y4=[0.08，0.06，0.24，0.09，0.26，0.04]

Y5=[0.06，0.07，0.19，0.08，0.27，0.26]

Y6=[0.37，0.10，0.06，0.21，0.03，0.06]

(四)利用灰色关联系统模型对融资模式进行排序

首先，将作为典型融资模式的内部融资的特征向量初始化，得到：

下一步，将其余6种融资模式的特征向量分别与内部融资的特征向量作差并求其绝对值得到：

Z1=|Y1-X|=[0.68,0.41,0.17,0.23,0.18,0.10]

Z2=|Y2-X|=[0.95,0.32,0.24,0.12,0.36,0.06]

Z3=|Y3-X|=[0.89,0.45,0.15,0.28,0.36,0.29]

Z4=|Y4-X|=[0.92,0.59,0.12,0.25,0.18,0.05]

Z5=|Y5-X|=[0.94,0.59,0.17,0.26,0.17,0.16]

Z6=|Y6-X|=[0.63,0.55,0.30,0.13,0.41,0.04]

于是

Δmax=max[0.68,0.95,0.89,0.92,0.94,0.63]=0.95

Δmin=min[0.10,0.06,0.15,0.05,0.16,0.04]=0.04

根据公式(8)，求得其余6种融资模式与内部融资的关联系数，如表8所示，其中ρ=0.5：

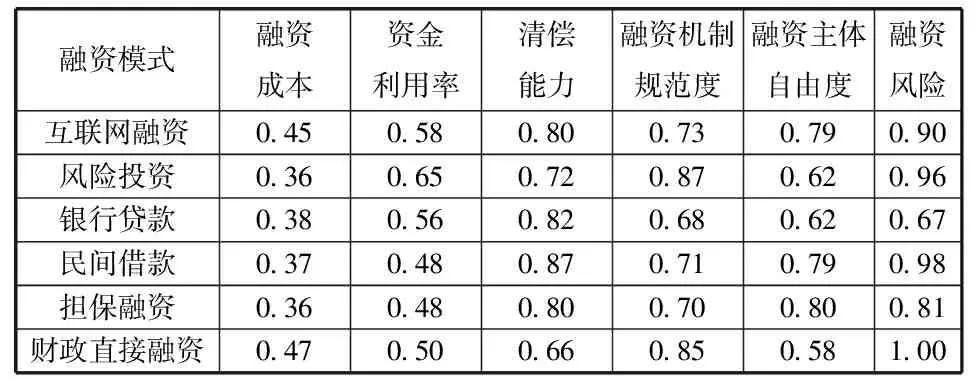
表8 关联系数计算结果

最后，根据公式(7)，通过计算得到其余6种融资模式与内部融资的关联度为：

表9 关联度计算结果

综上，通过对其余6种融资模式与内部融资的关联度的对比可得：M2>M3=M5>M7 >M6>M4。

从以上结果中我们可以看出，与内部融资模式关联度最大的是互联网金融这一新型融资模式，其次是风险投资与民间借款，而作为传统融资模式的银行贷款模式则位居末位。

五、结论

本文通过构建基于层次分析法与灰色关联度的综合评价模型，将互联网金融这一新型融资模式考虑进来，研究了青岛市科技型中小企业普遍采用的7种融资模式之间关联度的关系。结果表明，基于融资效率视角的融资模式的排序为内部融资、互联网金融、风险投资与民间借款、财政直接融资、担保融资、银行贷款。此研究结果为青岛市科技型中小企业在日后的融资模式选择上提供了新的思路。随着互联网金融的迅速发展，加之其审核时间短、放款速度快等优点，互联网金融越来越受到中小型企业家的青睐。除内部融资外，互联网金融很有可能成为日后青岛市科技型中小企业家的首选融资模式，而作为传统融资模式的银行贷款模式由于其对中小企业的融资需求审查过于严格且违约利息高等缺点，正在逐渐失去其在融资模式中的传统地位。

[1] Modigliani，Miller.The Cost of Capital，Corporate Finance and The Theory of Investment[J].American Economic Review，1958，48(3).

[2] 廖理，朱正芹.中国上市公司股权融资与债权融资成本实证研究[J].中国工业经济，2003，183(6).

[3] 曾康霖.怎样看待直接融资与间接融资[J].金融研究，1993，(10).

[4] 彭晓英，张庆华.基于DEA模型的煤炭上市公司股权融资效率评价[J].中国矿业，2008，17(12).

本课题受《青岛市科技金融的作用机制与模式创新研究》(项目号15-9-2-1-(8)-zhc)资助。