混凝土柱承载力按砌体柱计算的不合理性分析

林上顺，陈宝春

(1.福建工程学院福建省土木工程新技术与信息化重点实验室，福建 福州 350118；2.福州大学土木工程学院，福建 福州 350116)

混凝土柱承载力按砌体柱计算的不合理性分析

林上顺1，陈宝春2

(1.福建工程学院福建省土木工程新技术与信息化重点实验室，福建 福州 350118；2.福州大学土木工程学院，福建 福州 350116)

我国公路混凝土拱承载力计算通常将拱圈等效为梁柱后，按砌体柱公式计算承载力.通过混凝土柱和砌体柱轴压构件和偏压构件的破坏模式与计算方法进行对比分析，结果表明:混凝土柱的破坏模式、截面强度、偏心率折减系数、纵向弯曲系数与砌体柱均有所不同；混凝土柱截面强度采用砌体柱的强度计算将小于实际值；而混凝土柱纵向弯曲系数、偏心率折减系数均小于砌体柱.因此，混凝土偏压柱按砌体柱的计算方法计算将大于实际承载力，偏于不安全也不合理.混凝土柱的承载力应采用合理方法计算.

砌体柱；素混凝土柱；极限承载力

0 引言

拱桥是我国公路常用桥型之一.按主拱材料可分为等砌体拱(由块石或混凝土砌块(较少采用))和混凝土拱(含筋率不高的素混凝土拱或钢筋混凝土拱)两大类.拱面内承载力计算时，采用等效梁柱法.

《公路砖石及混凝土桥涵设计规范(JTJ 022-85)》[1](以下简称JTJ 022-85)给出了砌体柱的承载力计算方法，但没有给出素混凝土柱的承载力计算方法.《公路钢筋混凝土及预应力混凝土桥涵设计规范(JTJ 023-85)》[2](以下简称JTJ 023-85)给出了钢筋混凝土柱的承载力计算方法，也没有给出素混凝土柱的承载力计算方法.同时，JTJ 023-85第3.3.7条规定，钢筋混凝土拱的承载力计算也可按JTJ 022-85的相关规定进行.因此，在85版公路桥梁规范下,我国的混凝土拱桥多按照砌体拱桥的计算方法进行设计计算，如文[3-6]的算例计算.

《公路圬工桥涵设计规范(JTG D61-2005)》[7](以下简称为JTG D61-2005)中砌体柱的计算方法沿用了JTJ 022-85的计算方法，同时给出了混凝土柱的承载力计算方法.然而，由于文[5-6]近期没有再版，目前在实际的工程设计中，一般仍以文[5-6]为参考，采用砌体柱的计算方法来计算混凝土拱的承载力[8-10].

这种将混凝土柱视为砌体柱的计算方法的合理性，目前未见深入的探讨.本研究将对此展开分析讨论.

1 计算方法简介

JTJ 022-85给出的砌体柱稳定(承载力)计算公式:

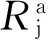
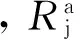
2 轴压构件

2.1 破坏模式

文[11]介绍了多功能空心砌块砌体受压柱从开始受压至破坏的过程，测力计的读数越来越不稳定，偏压砌体试件会有明显的变形，并伴随有崩裂和炸裂的声音，直到无法加载或试件破坏，此阶段为破坏阶段.破坏时，试件的裂缝多数沿着砌缝开展，而且以竖向裂缝为主，见图1.

图1 轴压砌体柱破坏模式[11]Fig.1 Failure mode of axially loaded masonry column[11]

图2 素混凝土轴压柱破坏模式Fig.2 Failure mode of axially loaded plain concrete column

混凝土轴压短柱的破坏，一般情况下只与混凝土材料的抗压强度有关.文[12]开展了素混凝土柱的轴压试验，从加载开始至破坏的过程大致也可分为弹性受力、裂缝发展与破坏3个阶段.随着荷载增大，试件裂缝出现多条不连续的短裂缝.当荷载接近承载力时，混凝土柱出现宏观斜裂缝，柱端混凝土表面开始出现剥落、掉块现象，试件内部主要存在纵向裂缝或称劈裂裂缝.试件破坏无明显预兆.素混凝土轴压柱的破坏照片见图2.与砌体柱不同的是，素混凝土柱的裂缝方向是不明确的，而砌体柱的裂缝开展方向是明确的，即首先沿着砌缝开展.

2.2 承载力计算方法

2.2.1 砌体轴压短柱的承载力计算方法

大量研究表明，砌体柱的截面强度不仅与砌块形状、尺寸、强度有关，且与砂浆强度有关[13-16].JTJ022-85和JTGD61-2005均以列表方式给出了相应砌体柱的截面强度，其强度值远低于砌块的强度.JTGD61-2005在条文说明中则给出了砌体强度的计算公式:

式中：fm为砌体的强度；f1为块材的抗压强度等级值或平均值；f2砂浆的抗压强度平均值.式(2)仅适用于采用普通砂浆砌筑的砌体，若砂浆强度达到一定值时，式(2)不再适用.假设f1和f2均取30.8 MPa，代入式(2)可得fm为31.7 MPa，大于f1，这显然是不合理的.因此，JTG D61-2005仅提供了砂浆强度不大于M20的砌体强度.

砌体柱的截面强度可表示为:

式中：A为砌体柱的截面积.

文[14]开展了混凝土小型空心砌块砌体的试验，其中包括40个偏压短柱(偏心率为0.1、0.2、0.3、0.4)和52个轴压(长细比6.3～15.8).试验结果表明，计算承载力时采用混凝土抗压强度是不合理的，而应采用砌体的抗压强度.

2.2.2 混凝土轴压短柱的承载力计算方法

根据文[17]，整体浇注的混凝土柱的抗压强度fc取值为0.8fcu(fcu为混凝土立方体抗压强度).则素混凝土柱的截面强度可表示为:

1)混凝土与砌体轴压短柱的承载力比较.根据式(4)，文[12]中编号为C1-3的试件的截面强度N0t为1.848 MN，其余18根试件的N0t为1.48 MN.

按式(2)和式(3)计算砌体柱承载力时，为进行同等程度比较，f1取值与式(4)的fc相同，f2按JTG D61-2005中砂浆强度等级的最大值取为M20.根据式(3)，编号为C1-3的试件的截面强度N0q仅为1.448 MN，其余试件的N0q仅为1.139 MN.N0q与N0t的比值约为0.77，换言之，混凝土柱承载力按砌体柱强度进行计算，强度取值偏小，可表示为：

2)混凝土柱视为砌体柱的算法与试验比较.按照式(1)，混凝土柱视为砌体柱承载力计算方法，即混凝土强度取式(4)中的fc，而承载力影响系数按式(1)计算，取式(1)中的偏心距为零.

文[12]进行了19根素混凝土柱承载力试验，其中5根轴压试件，14根偏压试件.试件为矩形截面，宽300 mm，高200 mm，主要参数有长细比和偏心率，试件详细资料见文 [12].

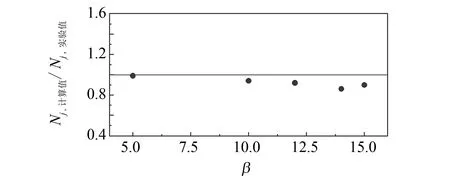
图3 轴压柱的比值Fig.3 Ratio of axially loaded specimens

将偏心率e为零代入式(1)中，即可得到轴压柱承载力计算式.如果再将长细比β为零代入，则得轴压短柱的计算式.

对文[12]中5根轴压试件采用砌体柱的承载力计算式计算，结果与试验值比较见图3.由图3知，采用这种算法得出的试件承载力均小于试验值.

2.2.3 轴压柱弯曲系数比较

1)砌体轴压柱的弯曲系数.若取偏心距为零代入式(1)，可得到砌体轴压柱的弯曲系数，

2)素混凝土轴压柱的弯曲系数.根据文[12]，素混凝土轴压柱的弯曲系数为：

比较式(6)和式(7)可知，砌体柱的弯曲系数与砂浆的强度有关，而素混凝土柱的弯曲系数与混凝土的强度无关.

3 偏压构件

3.1 破坏模式

文[17]介绍了砌体偏压短柱的破坏过程.当荷载加至破坏荷载的70%左右时，一些试件是刀铰下方附近的正面(宽度方向)出现第一条竖向裂缝；继续加载，竖向裂缝亦不断增多，但是远离刀铰一侧的侧面(高度方向)上一直未有竖向裂缝出现；当荷载达到极限荷载时，竖向裂缝基本贯通，如图4所示.

图5显示了素混凝土偏压短柱的破坏照片，其裂缝以水平向裂缝为主，与砌体柱以竖向裂缝为主有明显的不同，混凝土被压碎或拉裂的区域一般集中在试件的中点附近.

图4 砌体偏压柱破坏模式[13]Fig.4 Failure mode of eccentrically loaded masonry column[13]

图5 素混凝土偏压柱破坏模式[11]Fig.5 Failure mode of eccentrically loaded plain concrete column[11]

3.2 混凝土柱视为砌体柱的算法与试验比较

取文[12]中14根偏压试件，按2.2.4节方法(式(1))计算其承载力.对于试件，不考虑材料安全系数的影响，整体浇注的混凝土柱的抗压强度fc按文[17]取值为0.8fcu(fcu为混凝土立方体抗压强度)，按照上一节计算方法计算的14根素混凝土偏压柱的承载力与试验值对比见图6.仅个别试件承载力计算值与试验值较接近，大部分试件的承载力计算值大于试验值，这显然是偏于不安全的.

3.3 偏心率影响系数比较

由于破坏模式不同，素混凝土短柱的偏心影响系数与砌体短柱有所差别.根据文[12]，素混凝土短柱的偏心率影响系数可由下式表示，它与式(1)显然有所不同.

文[18]进行了3根编号为PA3-1、PA3-2、PA3-3,长细比为3.0的素混凝土偏压短柱试验.图7示出了这3根试件的试验值与式(2)、式(8)的比较情况.从图中可知，试验值与式(8)较接近，而小于式(1)的计算结果.

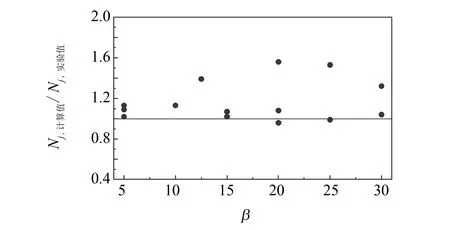
图6 偏压柱的比值Fig.6 Ratio of eccentrically loaded specimens

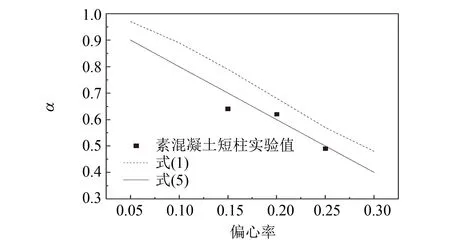
图7 素混凝土短柱偏心影响系数对比图Fig.7 Comparison on the eccentric influence coefficient of short plain concrete columns

3.4 承载力影响系数比较

JTJ 022-85的砌体柱和文[12]中的素混凝土柱，其承载力影响系数均为纵向弯曲系数与偏心率影响系数的乘积.文[12]给出了混凝土柱的弯曲系数：

式中：β为构件长度与截面高度的比值，当β≤3时，取β=3.在承载力计算中，纵向弯曲系数与混凝土强度等级无关.

图8 承载力比值Fig.8 Ratio of the specimens

比较式(9)与式(1)中的承载力影响系数，显然两式是不同的.在砌体柱的承载力影响系数中，α′ 是与砂浆强度有关的系数，对于混凝土，α′ 取为0.002.而式(9)与混凝土的强度无关.

图8示出文[12]中偏心率为0.2的试件承载力影响系数试验值和按砌体柱算出的结果.可见，按砌体柱算出的承载力影响系数均大于试验值.文[12]中其他试件的情况也类似，这里不再一一示出.

若以φ01表示砌体柱承载力影响系数，以φ02表示素混凝土承载力影响系数，则:φ01>φ02.

3.5 偏压柱承载力计算结果综合比较

各种算法可用下列算式表示:

砌体偏压柱算法：Nu1=φ01N0q

素混凝土偏压柱算法：Nu2=φ02N0t

混凝土柱视为砌体柱的算法：Nu3=φ01N0t

其中：Nu3>Nu2>Nu1.

从以上分析可知，整体浇注的素混凝土偏压柱截面强度大于混凝土预制块砌体偏压柱的截面强度，而整体浇注的素混凝土柱承载力影响系数一般小于混凝土预制块砌体柱.

在进行素混凝土偏压柱承载力设计计算时，若截面强度采用整体浇注的素混凝土柱，而承载力影响系数却采用混凝土预制块砌体柱，则算出的承载力结果往往偏大，偏于不安全.因此，素混凝土偏压柱承载力设计计算，无论是截面强度还是承载力影响系数，均应按素混凝土偏压柱的承载力计算公式进行.

4 进一步讨论

上述分析表明，混凝土柱按照砌体柱进行承载力计算是不合理的.JTGD61-2005已经提供了素混凝土柱的承载力计算公式.混凝土柱的承载力按该方法计算是否就可以解决混凝土柱按照砌体柱计算所存在的问题呢？

文[19]对文[20]的4根素混凝土试件采用JTGD61-2005的计算方法所得到的承载力，与试验值相比有较大差异，且其中三个试件的计算结果大于试验值，偏于不安全.为此，文[12]完成了19根素混凝土偏压柱的承载力试验研究，进一步证实了文[19]的结论.分析表明，JTGD61-2005给出的素混凝土柱承载力计算公式采用稳定系数与偏心率修正系数分离的算法，没有考虑二者的耦合作用，是导致其在长细比较大、偏心率较大时，计算的承载力较实际承载力大的主要原因[12].

从文[1]可知，其所给出的混凝土柱承载力计算，其试验结果与有限元参数分析结果吻合较好，可供实际工程应用与规范修订时参考.

5 结语

1)砌体柱的截面强度不仅与砌块形状、尺寸、强度有关，且与砂浆强度有关.混凝土轴压短柱的破坏，一般情况下只与混凝土材料的抗压强度有关.混凝土砌体柱截面强度采用混凝土抗压强度将大于实际值.反过来，混凝土(整体)柱截面强度采用砌体柱的强度计算则小于实际值.

2)对于轴压长柱，砌体柱的弯曲系数与砂浆强度有关，而素混凝土柱的弯曲系数与混凝土强度无关.

3)砌体偏压短柱破坏与竖向砌缝开裂有关，而混凝土偏压短柱破坏时主要是中点附近混凝土被压碎或拉裂.因此，二者的偏心率影响系数也不同.混凝土偏压短柱采用砌体柱的偏心率影响系数计算的承载力将大于实际值.

4)混凝土偏压长柱承载力影响系数均可用纵向弯曲系数与偏心率影响系数的乘积表示，但二者表达式不一致.采用砌体柱承载力影响系数计算混凝土偏压长柱的承载力将高于实际承载力，偏于不安全.

因此，混凝土柱承载力计算时按砌体柱的计算方法是不合理的.JTGD61-2005提供的素混凝土柱承载力计算公式，采用稳定系数与偏心率修正系数分离的算法，没有考虑二者的耦合作用，将使其计算结果在长细比较大、偏心率较大时，较实际承载力大而偏于不安全.建议素混凝土柱的承载力计算，采用文[12]提出的计算方法.

[1] 中华人民共和国交通部.公路砖石及混凝土桥涵设计规范:JTJ022-85[S].北京:人民交通出版社，1985.

[2] 中华人民共和国交通部.公路钢筋混凝土及预应力混凝土桥涵设计规范:JTJ023-85[S].北京:人民交通出版社，1985.

[3] 王国鼎，钟圣斌.拱桥[M].2版.北京：人民交通出版社，2000.

[4] 杨稚华.万县长江大桥的设计[C]//四川省公路学会桥梁学会研讨会论文集.成都：西南交通大学出版社，1996．

[5] 顾安邦，孙国柱.公路桥涵设计手册：拱桥(下册)[M].北京：人民交通出版社，1994.

[6] 顾懋清，石少甫.公路桥涵设计手册:拱桥(上册)[M].北京：人民交通出版社，1996.

[7] 中华人民共和国交通部.公路圬工桥涵设计规范:JTGD61-2005[S].北京:人民交通出版社,2005.

[8] 张杰.福建宁德岭兜特大桥设计[J].中外公路,2008,28(5)：167-170.

[9] 胡江顺,陈四德,苏明星.双潭大桥:座钢筋混凝土拱桥设计[J].中外公路,2008，28(4)：156-159.

[10] 尹超.大跨度上承式钢筋混凝土箱肋拱桥设计[J].华北水利水电学院学报，2010，31(1)：41-44.

[11] 杨伟军，祝晓庆，马丽慧.多功能混凝土空心砌块砌体受压承载力试验研究[J].长沙交通学院学报,2006，22(1)：32-35.

[12] 林上顺,陈宝春.素混凝土柱极限承载力计算方法[J].交通运输工程学报,2015,15(2):22-31.

[13] 徐春一.蒸压粉煤灰砖砌体受力性能试验与理论研究[D].大连：大连理工大学,2011.

[14] 钱义良，施楚贤.砌体结构设计规范GBJ3-88背景资料[C]//砌体结构研究论文集.长沙：湖南大学出版社,1989:18-23.

[15] 孙氰萍，周维彦.小型空心砌块的材性与砌体的基本力学性能[J].四川建筑科学研究,1980(1):13-25.

[16] 中华人民共和国建设部.砌体结构设计规范：GB50003-2001[S].北京:中国建筑工业出版社，2001.

[17] 过镇海，时旭东.钢筋混凝土原理和分析[M].北京：清华大学出版社,2011.

[18] 偏心受压构件强度专题研究组.钢筋混凝土结构研究报告选集(2)[R].北京：中国建筑工业出版社,1981：19-60.

[19] 陈宝春，林上顺.混凝土偏压柱承载力计算方法[J].交通运输工程学报，2014，14(1)：18-25.

[20] 王引富,刘汉夫.铁路圬工桥墩临界荷载的非线性分析[J].石家庄铁道学院学报,1996,9(3):69-73.

(责任编辑：沈芸)

Analysison the unreasonable of the calculation methods for the load bearing capacity of concrete columns as masonry ones

LIN Shangshun1,CHEN Baochun2

(1.Fujian Provincial Key Laboratory of Advanced Technology and Informatization in Civil Engineering,Fujian University of Technology,Fuzhou,Fujian 350118,China；2.College of Civil Engineering,Fuzhou University,Fuzhou,Fujian 350116,China)

In the bearing capacity calculation methods of highway concrete arch in our country,when the arch is equivalent to beam-column,the formulas of masonry column are often used to estimate the load bearing capacity of the concrete arch.For the irrationality of this method,through the analysis and comparison of the the failure modes and calculation methods of axial compression member and eccentrically loaded member between concrete column and masonry column,the results show that the the failure modes,the intensity of cross section and the eccentricity reduction factors as well as the buckling coefficients of reinforced concrete columns are different from that of masonry columns ；if the formulas of masonry column are used to estimate the intensity of cross section of concrete column,the result will be smaller than the actual value；however the buckling coefficients and the eccentricity reduction factors of concrete column are smaller than that of masonry column.therefore,if the formulas of masonry column are used to estimate the eccentrically loaded concrete columns,the results will be greater than the actual value,which is unsafe and unreasonable,the calculation of the bearing capacity of the concrete column should adopt reasonable calculation methods.

masonry column; plain concrete column; ultimate load bearing capacity

10.7631/issn.1000-2243.2017.02.0173

1000-2243(2017)02-0173-06

2015-12-02

林上顺(1972-)，副教授，主要从事大跨度桥梁结构研究，578982122@qq.com

国家自然科学基金资助项目(U1305245)

U448.22; U441

A