独塔部分斜拉桥顺桥向地面运动作用下的易损性分析

吴少峰，上官萍，姜绍飞

(福州大学土木工程学院，福建 福州 350116)

独塔部分斜拉桥顺桥向地面运动作用下的易损性分析

吴少峰，上官萍，姜绍飞

(福州大学土木工程学院，福建 福州 350116)

以墩塔梁固结的独塔预应力混凝土部分斜拉桥为对象，采用动力增量法和数据统计分析研究该类桥梁的地震易损性，确定顺桥向地面运动作用下结构构件的易损部位及损伤破坏概率.采用理论易损性分析方法，选取地面峰值加速度作为地震输入强度指标，并以放大系数为基础选取地震输入；以位移延性比、强度与变形、相对位移、索力为指标分别定义了各构件的损伤状态；根据各构件的损伤概率，拟合建立了各构件及全桥的易损性曲线.结果表明，在顺桥向地面运动作用下，中墩和支座为最易损构件；边墩、主梁均会发生不同程度的损伤；斜拉索、桥塔、桩基安全储备较高.

独塔部分斜拉桥；地面运动；地震易损性；易损性曲线；损伤极限状态

0 引言

部分斜拉桥是连续梁桥与斜拉桥组合的一种新型桥梁结构体系，由主梁、塔与斜拉索等受力构件组合而成，兼有两种结构的优点，经济、新颖、美观、施工技术成熟.国内外已建成和在建的部分斜拉桥超过120座[1]，但是部分斜拉桥尚未遭遇较大的地震，构件破坏损伤的部位、程度和概率都不明确.因此，对部分斜拉桥进行地震易损性分析，明确结构构件的易损部位、损伤程度和概率，建立结构构件和整桥的理论易损性曲线，对其抗震性能设计和评估具有重要意义.部分斜拉桥结构形式灵活，根据工程需要设计成独塔、双塔或多塔形式.同时，墩塔梁也有多种连接方式，从结构形式最简单的独塔墩塔梁固结部分斜拉桥入手来研究其地震易损性.

关于桥梁的易损性研究，迄今有二十多年，一般探讨其易损性曲线的形成过程.目前，国内外主要采用的研究方法有：经验分析法、理论分析法以及其他方法[2-4].由于缺乏部分斜拉桥的震害资料，采用理论分析法，即通过对结构进行数值计算分析得到桥梁结构的地震易损性曲线，有非线性静力分析方法和非线性动力分析方法，本研究采用后者.要形成易损性曲线，必须建立在桥梁结构的地震动力特性的基础上，先依次完成地震动的模拟，考虑桥梁不确定性对桥梁结构的模拟，获得桥梁结构的地震反应分析，再与损伤指标对比，利用统计分析理论，最终形成易损性曲线.

1 工程背景和有限元模拟

1.1 工程简介

已建的独塔部分斜拉桥有40多座，跨度基本在50～150 m之间，塔高一般在20 m左右，大部分采用扇形双索面，墩塔梁固结的较多，综上，选取福建仙港大桥主桥为基准桥.该桥全长120 m，跨径布置为60 m+60 m，桥宽16.25 m，主塔为双柱形独塔，扇形双索面，总体布置如图1所示.主梁为变截面箱梁，梁高为1.6～2.5 m；桥塔高22 m，纵向变宽3.0～5.5 m，横向宽1.5 m；每个索面6对拉索对称布置；中墩为双柱墩，纵向宽3 m，横向宽1.5 m；边墩为单柱墩，纵向宽1.2 m，横向宽3 m；基础为钻孔灌注桩，桩径1.5 m，桩长按20 m考虑；承台尺寸为7.5 m7.5m3 m，承台下设4根桩，两个承台用截面尺寸为3 m3 m系梁连接.混凝土除边墩采用C40、基础采用C30外，其他均采用C50；斜拉索采用环氧全涂PC钢绞线索，极限强度1.860 GPa

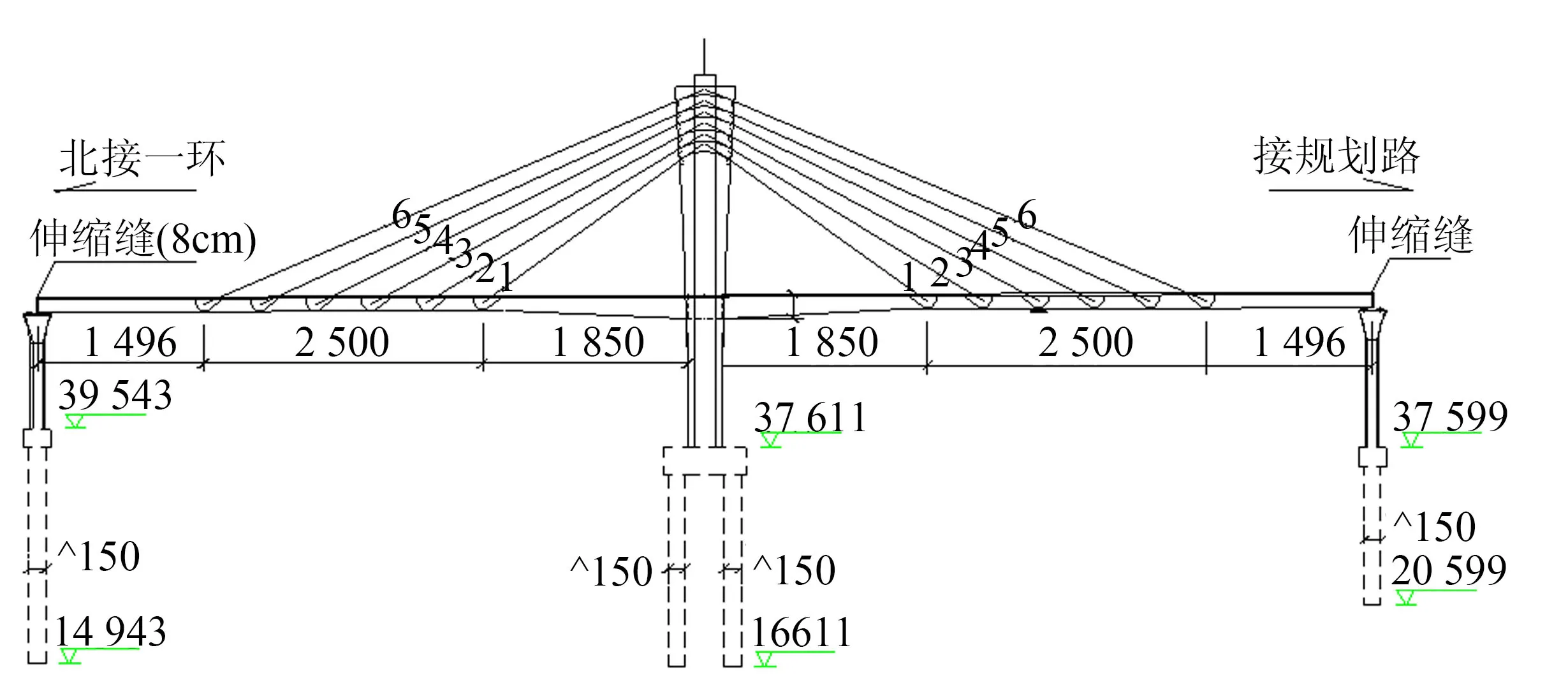
图1 总体结构布置图(单位：cm)Fig.1 Bridge type and structure of the main bridge(unit：cm)

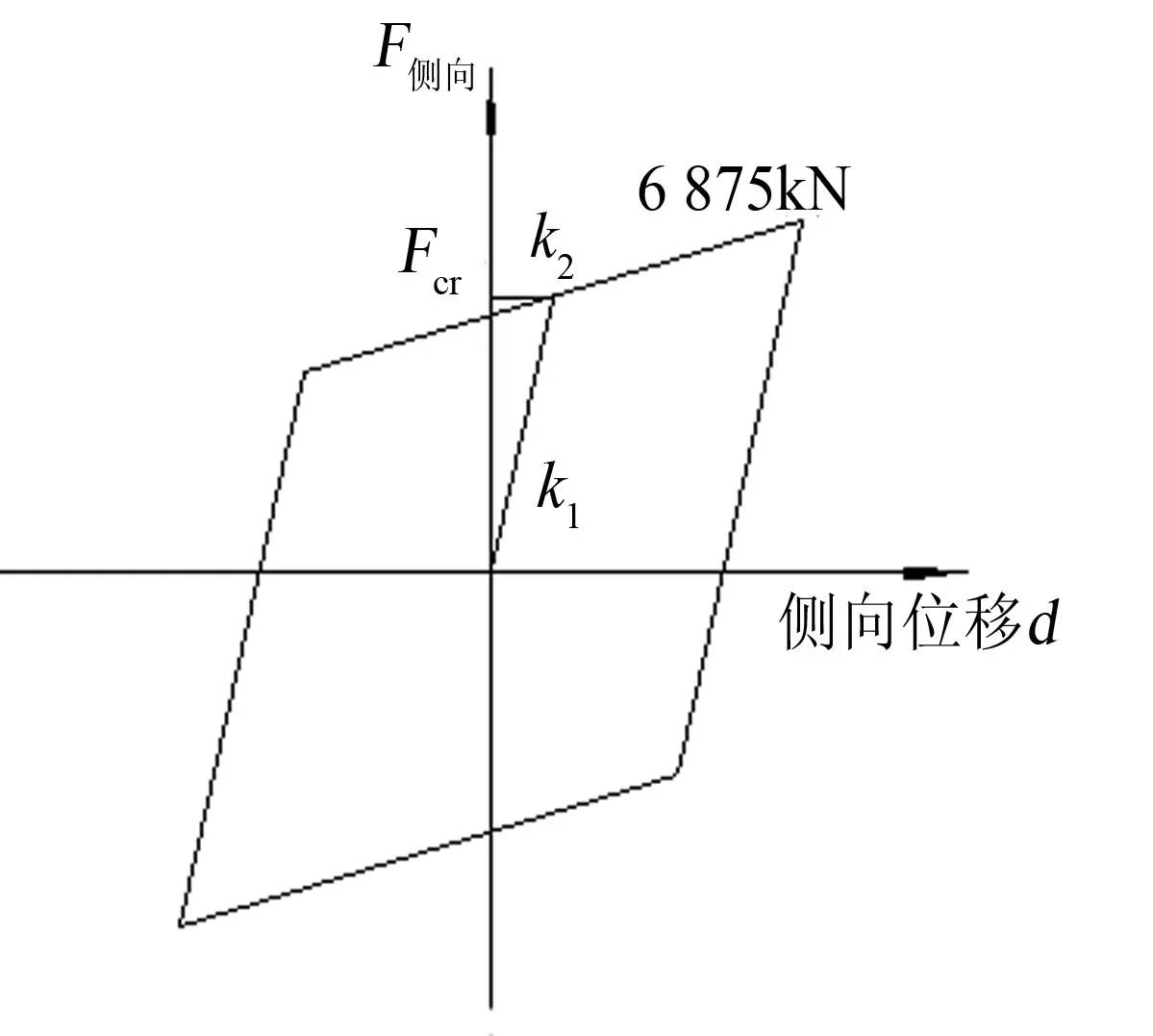
图2 板式滑动支座的恢复力模型Fig.2 Resilience modle of the elastomeric bearing pads

1.2 有限元建模及模型修正

采用MIDAS建立基准桥的有限元模型，为准确模拟构件状态和提高计算效率，对五个构件分别采用三种不同的单元模拟.由于地震输入的强度较大，构件有可能进入弹塑性阶段，对构件的易损部位的单元采用了非弹性单元模拟，支座恢复力模型如图2所示.

1)主梁、墩、塔的模拟.均采用弹性三维梁单元模拟，通过共用节点实现墩塔梁的刚接，主梁简化成“鱼刺梁”模型.顺桥向地面运动作用下，塔底、中墩墩底和墩顶、边墩墩底为各构件的易损部位，地面运动强度较大的工况会进入弹塑性阶段，故相关工况需采用非弹性铰单模拟.根据文献[5]的研究，在顺桥向地面运动大于0.2g时，主梁开始会进入弹塑性阶段，故其易损部位在大于0.2g的工况下采用非弹性铰单元模拟.

2)承台和基础的模拟.承台的作用视为刚性连接，自重通过在桩顶施加节点重量模拟.桩基用弹性三维梁单元模拟，考虑桩土效应，采用M法求取土弹簧的刚度Ks[6].

3)拉索的模拟.采用柔性索单元模拟，通过斜拉索弹性模量的折算来考虑索的非线性影响.由于索的长度较短，恒载索力占总索力的比重大，经计算，弹性模量通过折算后没有变化.

4)支座条件的模拟.边墩上采用板式滑动支座，在常规的地震反应中，板式滑动支座的恢复力-位移模型采用双线性Clough模型[7-8]，如图2所示.根据弹性恢复力最大值与临界滑动摩擦力相等的条件，可得临界位移值为xy=fN/K，其中，f为滑动摩擦系数；N为承担的上部结构恒载.

5)非弹性铰单元模拟.独塔部分斜拉桥动力特性表现出二维性和相对独立性[1]，相关工况下，主梁近跨中段、墩底、塔底、中墩顶等易损部位的截面仅考虑在顺桥向进入弹塑性状态，并设置塑性铰.铰单元长度均按Caltrans规范[9]的公式Lp=0.08l+0.022fyedbl≥0.04fyedbl取值；骨架线由截面弯矩-曲率分析确定，图3为采用Ucfyber分析得到的中墩墩顶、墩底两个截面的弯矩-曲率曲线；滞回模型采用双线性Clough模型[10].

基于以上简化，建立有限元模型如图4所示.通过材料弹性模量、预应力损失、收缩徐变等试验，对相关参数进行识别，对模型的混凝土弹性模量、预应力、收缩徐变和结构自重进行修正[10]；通过现场实测的背景桥的自振频率和振型，对结构的刚度和边界条件进行修正.使模型的内力状态及动力特性与实测的相吻合，以确保模型的有效性.

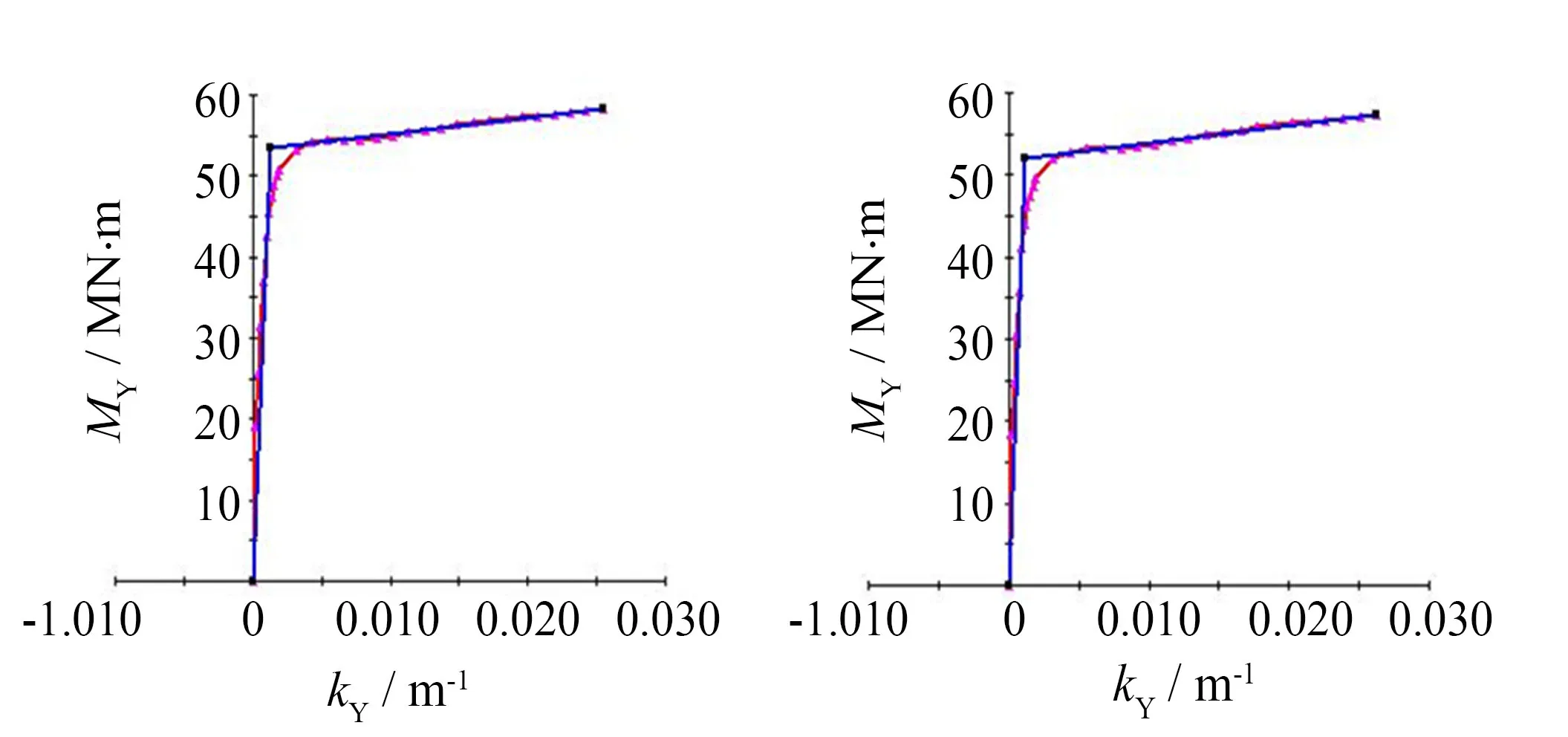
图3 中墩墩底和墩顶弯矩-曲率图Fig.3 Moment-curvetures chart of middle pier’s upper and bottom section

图4 基准桥有限元模型Fig.4 Finite-element analysis modle of xian gang bridge

2 易损性分析

2.1 地面输入

结构易损性重点分析地面运动输入、抗震能力、地震需求三个参数.地面运动输入模拟，要选取适当的参数，并模拟地面运动的不确定性.考虑独塔部分斜拉桥的动力特性，经过对比，选取地面峰值加速度PGA作为强度指标.以地震波的放大系数均值为基础，综合考虑场地特征、震中距、振幅、频谱特性、持续时间等因素，从1989年Loma Prieta地震、1987年Whittier地震、1985年Michoacan地震、1971年San Fernando等地震中对照《公路工程抗震规范(JTGB 02-2013)》[11]选取50条地震波来模拟地面运动输入.

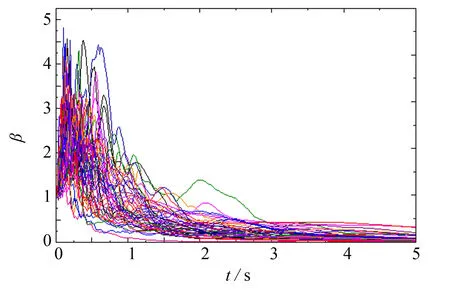
图5 地震波动力放大系数图(阻尼比=5%)Fig.5 Dynamic amplifying factors of the selected earthquake waves

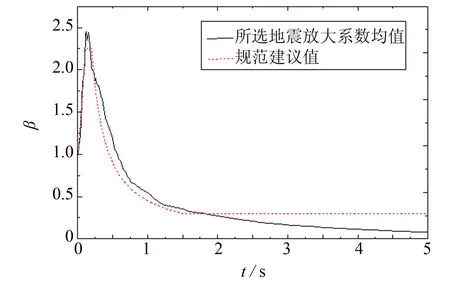
图6 地震波放大系数均值与规范值对比图Fig.6 Dynamic amplifying factors comparison chart between the selected earthquake waves and the standard

图5是选取的50条地震波的动力放大系数β谱(阻尼比=5%)，所选地震波的动力放大系数β的离散性较大；图6为50条地震波放大系数的均值曲线与规范I类场地建议值的对比图，可见，T=0～2 s时，所选地震波的动力放大系数均值基本大于规范值，但总体数值较为接近；T=3～5 s时，所选地震波动力放大系数均值小于规范值，T越大，偏差越大.鉴于基准桥的自振周期在1～2 s间，选用的地震波符合要求.

2.2 抗震能力分析

地面运动输入确定后，需要分析构件的抗震能力，即确定以构件的需求参数为条件的各级损伤极限状态模型.由于结构的随机性相对于地面运动的随机性小，故本研究假定结构的抗震能力为定值.

2.2.1 墩柱损伤极限状态的定义

构件的损伤极限状态与破坏模式有关，由文献[9]提供的公式可判断基准桥墩柱塔的破坏模式均属于弯曲破坏.采用UCfyber对墩柱塔易损部位的截面进行弯矩-曲率分析，可获得首次屈服、等效屈服、εc=0.004、极限屈服等关键值如表1所示.分别采用《earthquake loss estimation methodology technical manua(HAZUS 99)》[12]和Mackie[13]建议的位移延性比指标μ来定义墩柱塔的损伤等级和量化指标，其中首次屈服的位移延性比定义为1.同时定义首次屈服即发生轻微破坏，等效屈服即发生中等破坏，εc=0.004时即发生严重破坏，达到极限曲率即完全破坏，可得出损伤指标与损伤等级之间的关系如表2所示.

表1 墩塔各截面弯矩-曲率关系表Tab.1 Moment-curvetures relationship of separately section (rad·m-1)

表2 墩塔各截面各级损伤极限状态表Tab.2 Fullest extent of every damage on separately section

2.2.2 主梁损伤极限状态的定义

部分斜拉桥的主梁由于与边墩的支承关系不明确，不能确定延性位移比的计算模型；同时经过非线性动态时程分析可知顺桥向地面运动作用下[5]，主梁的易损部位在离塔第四根索到离塔第五根索之间的近跨中段，塑性铰长度难以确定.故本研究采用Hwang等[14]确定的强度与变形双指标定义主梁的损伤状态及量化指标，损伤状态定义与墩柱相同.经过近跨中段主梁截面的弯矩-曲率分析，可得近跨中段主梁的弯矩-曲率关系及各级损伤的极限状态如表3～4所示.

表3 梁近跨中截面弯矩-曲率关系表Tab.3 Moment-curvetures relationship of the beam section

φ截面表示截面曲率,M表示弯距

表4 近跨中梁各级损伤极限状态表Tab.4 Fullest extent of every damage on the beam

2.2.3 支座损伤极限状态的定义

基准桥边墩采用滑板橡胶支座.按照《公路桥梁板式橡胶支座(JT/T4-2000)》[15]的相关规定，确定其设计承载力、允许承载力和顺桥向最大位移.采用强度准则和位移准则作为支座的损伤指标.表5是本研究定义的支座各级损伤极限状态.其中Δbear表示支座顶部与底部的相对位移.

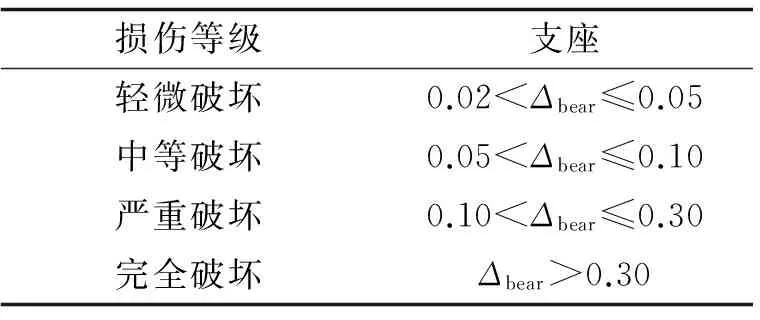
表5 支座各级损伤极限状态表Tab.5 Fullest extent of every damage on the bearing (m)

表6 斜拉索各级损伤极限状态表Tab.6 Fullest extent of every damage on the cable (MPa)

2.2.4 斜拉索损伤极限状态的定义

2.3 地震需求分析

采用增量动力分析方法[16]来分析背景桥在特定的地面运动强度下结构需求参数的概率特征.采用两个假定：一是假定在不同工况下各构件的易损部位保持不变；二是在地面运动强度下，各构件的响应可通过对数正态分布进行很好的拟合，假定各构件损伤概率服从对数正态分布[17].

为形成理想的地震易损性曲线，将地面运动的峰值加速度变化范围调整为0.05g～0.60g，分12种工况，每个工况峰值加速度按0.05g递增；各级工况50条地震波的峰值加速度调至相等强度输入计算，可得桥梁结构在给定地面运动强度下的结构需求.同时，通过各构件的需求与其各级损伤极限状态的对比，当需求大于某种损伤的极限状态，则该构件发生某种损伤，并设定构件发生完全破坏也发生严重破坏、中等破坏和轻微破坏，以此类推.经计算分析，在给定地面运动下各构件的损伤概率如表7～12所示.桥塔、桩基在地面运动作用下，均处在弹性范围内，未发生损坏，桩基最大内力出现在桩顶附近.

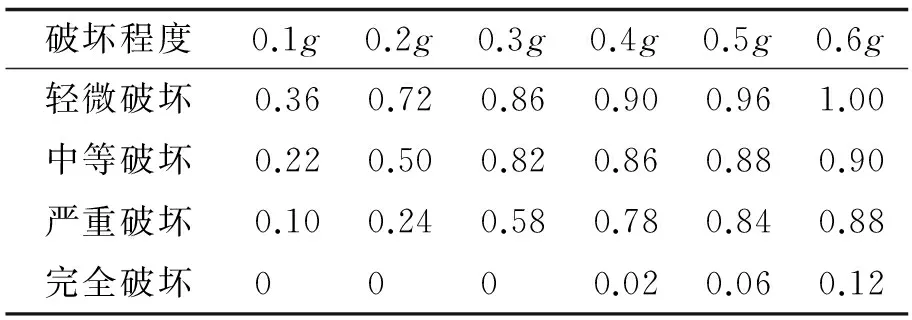
表7 中墩各级损伤概率表Tab.7 Probability of the middle pier for each level damage

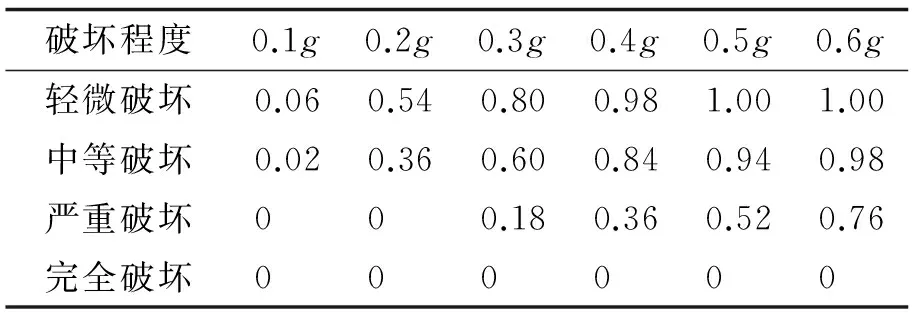
表8 边墩墩底截面各级损伤概率表Tab.8 Probability of the side pier for each level damage

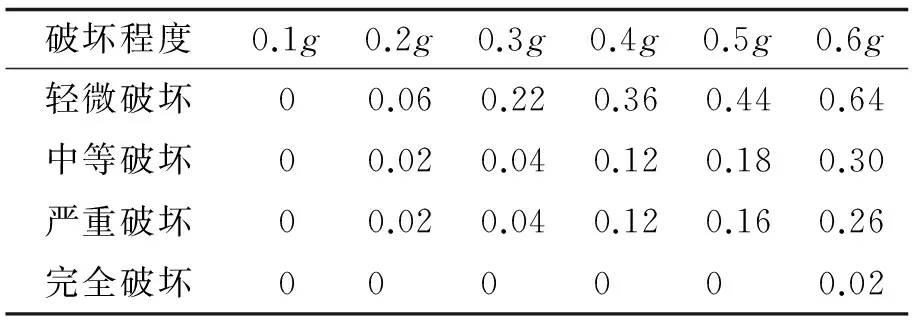
表9 近跨中梁截面各级损伤概率表Tab.9 Probability of the beam for of each level damage

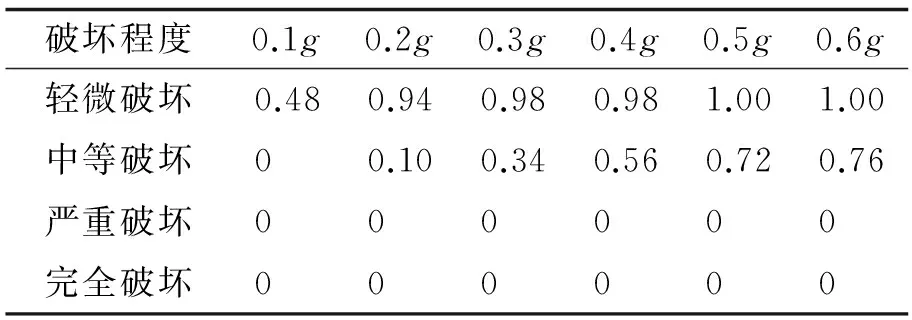
表10 支座各级损伤概率表Tab.10 Probability of the bearing for each level damage

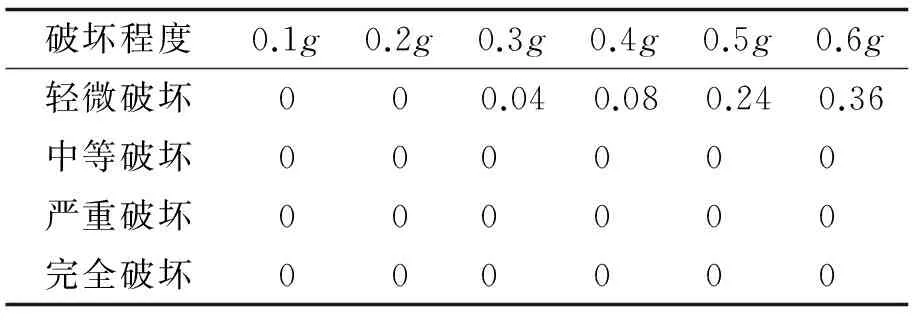
表11 斜拉索各级损伤概率表Tab.11 Probability of the cable for each level damage

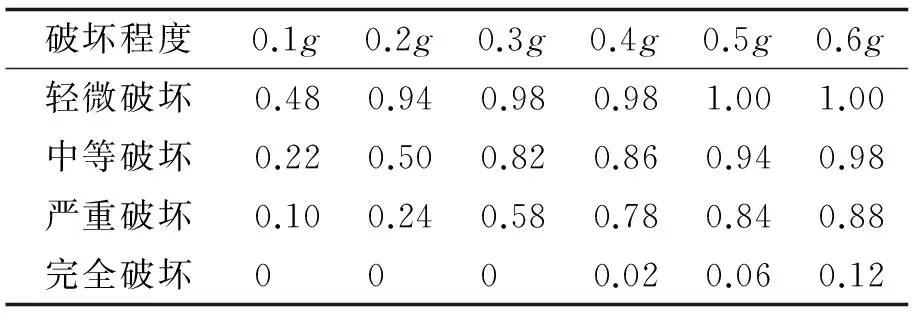
表12 全桥各级损伤概率表Tab.12 Probability of the bridge for each level damage

3 易损性曲线

易损性曲线传统定义为在特定的地面运动强度作用下，结构遭受特定状态损伤的超越概率；它是在对结构地震反应进行分析基础上，用于研究结构超过某种破坏状态的概率.按照形成易损性曲线的对象的不同，可划分为基于结构整体损伤指标的地震易损性分析和基于结构局部构件损伤指标的地震易损性分析.采用统计分析原理，对各构件的损伤概率离散点进行回归拟合，可得到概率密度函数的参数，由拟合的参数可以建立各构件的易损性曲线.对于全桥的地震易损性曲线，根据各个构件的重要性不同，参照《公路桥梁技术状况评定标准(JTG TH21-2011)》[18]的构件权重系数，加权得到全桥各状态的损伤概率，进而求其易损性曲线.

3.1 构件易损性曲线

3.1.1 中墩易损性曲线

对表7的损伤概率离散点用MATLAB中的lsqcurvefit函数进行回归拟合，可得到概率密度函数的拟合参数，根据拟合参数用MATLAB中的logncdf函数可以建立中墩易损性曲线如图7所示.“*”、“□”、“◇”、“+”分别表示中墩在不同强度地面运动作用下，发生轻微、中等、严重、完全损伤的概率(下同).由于中墩墩底的易损性高于墩顶，故以墩底的易损性曲线代表中墩的易损性曲线.从图7中可以看出各曲线与损伤概率点接近，说明对数正态分布假定较为合理.

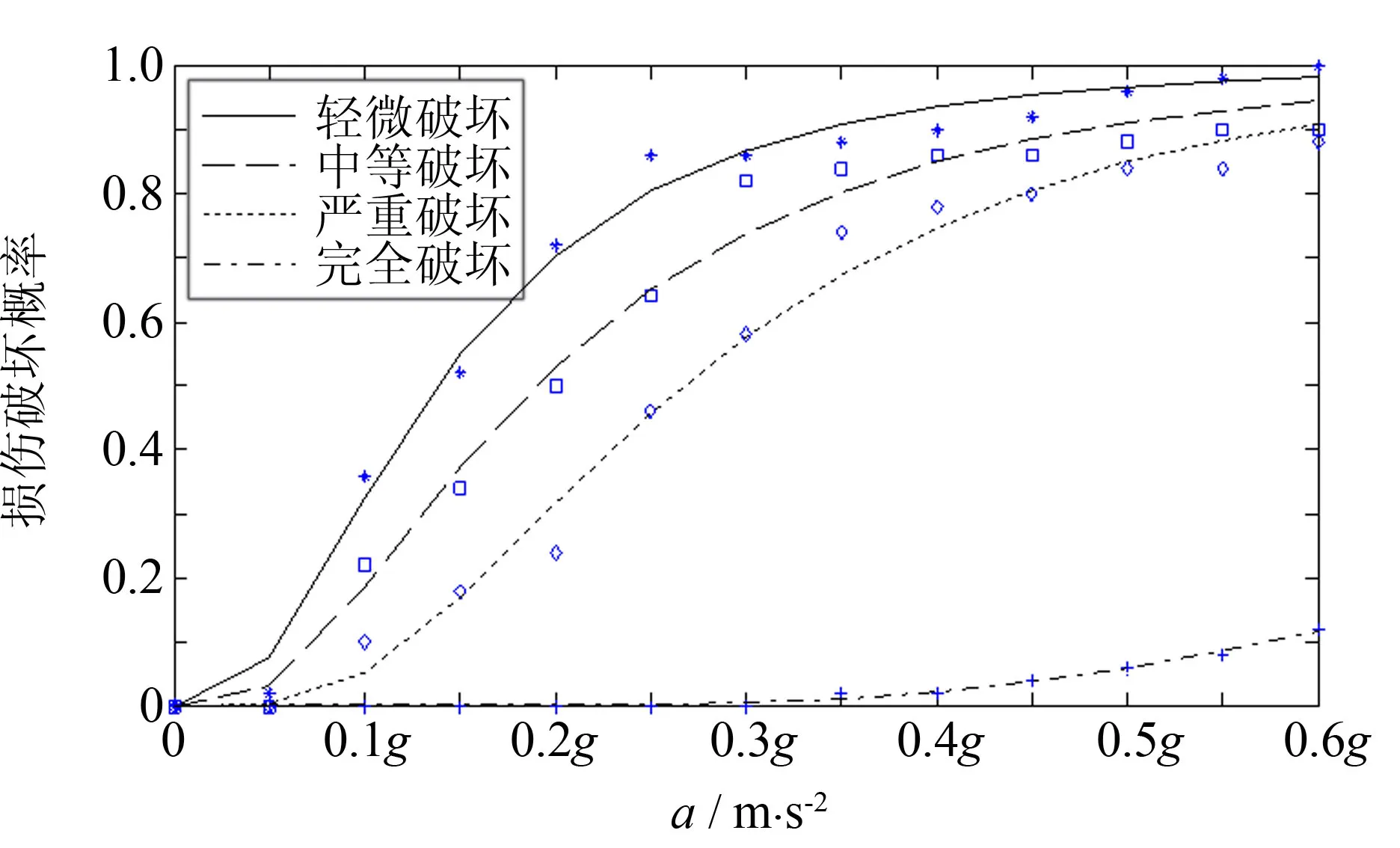
图7 中墩易损性曲线图Fig.7 Fragility curve for the middle pier

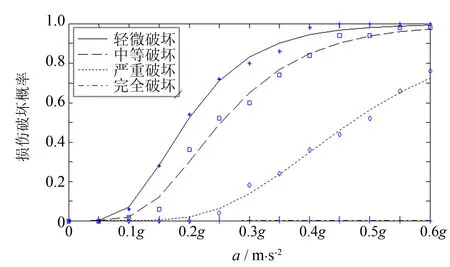
图8 边墩易损性曲线图Fig.8 Fragility curve for the sade pier

3.1.2 边墩易损性曲线

对表8的损伤概率离散点进行回归拟合，可得到概率密度函数的拟合参数，根据拟合参数用作出边墩的易损性曲线如图8所示.左边墩的易损性高于右边墩，故用左边墩的易损性曲线代表边墩的易损性曲线.根据张菊辉等[2]的研究，顺桥向地面运动作用下，墩高在15～25 m范围内，墩柱损伤的概率随墩高的增大而减小.基准桥右边墩比左边墩高，故边墩的损伤规律比较合理.边墩各类损伤概率接近但均低于中墩，且不会出现完全破坏.

3.1.3 主梁的易损性曲线

对表9的损伤概率离散点进行回归拟合，可得到概率密度函数的拟合参数，根据拟合参数可以作出主梁的易损性曲线如图9示.主梁的易损性曲线比较平坦，说明主梁的破坏概率相对中墩、边墩比较低，但不能忽略主梁的易损性，当主梁进入弹塑性后，整个结构的刚度矩阵会发生较大变化，从而影响其他构件的地震响应[5].图9中，中等破坏和严重破坏两条曲线很接近，是因为主梁的延性较小，可能发生弯剪破坏，所以两种破坏形式的分界不明显.

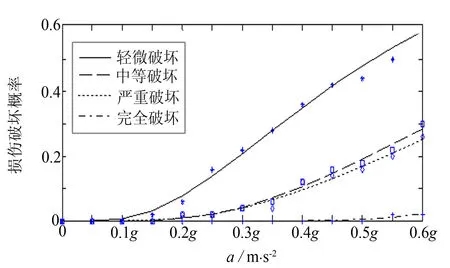
图9 主梁易损性曲线图Fig.9 Fragility curve for the beam

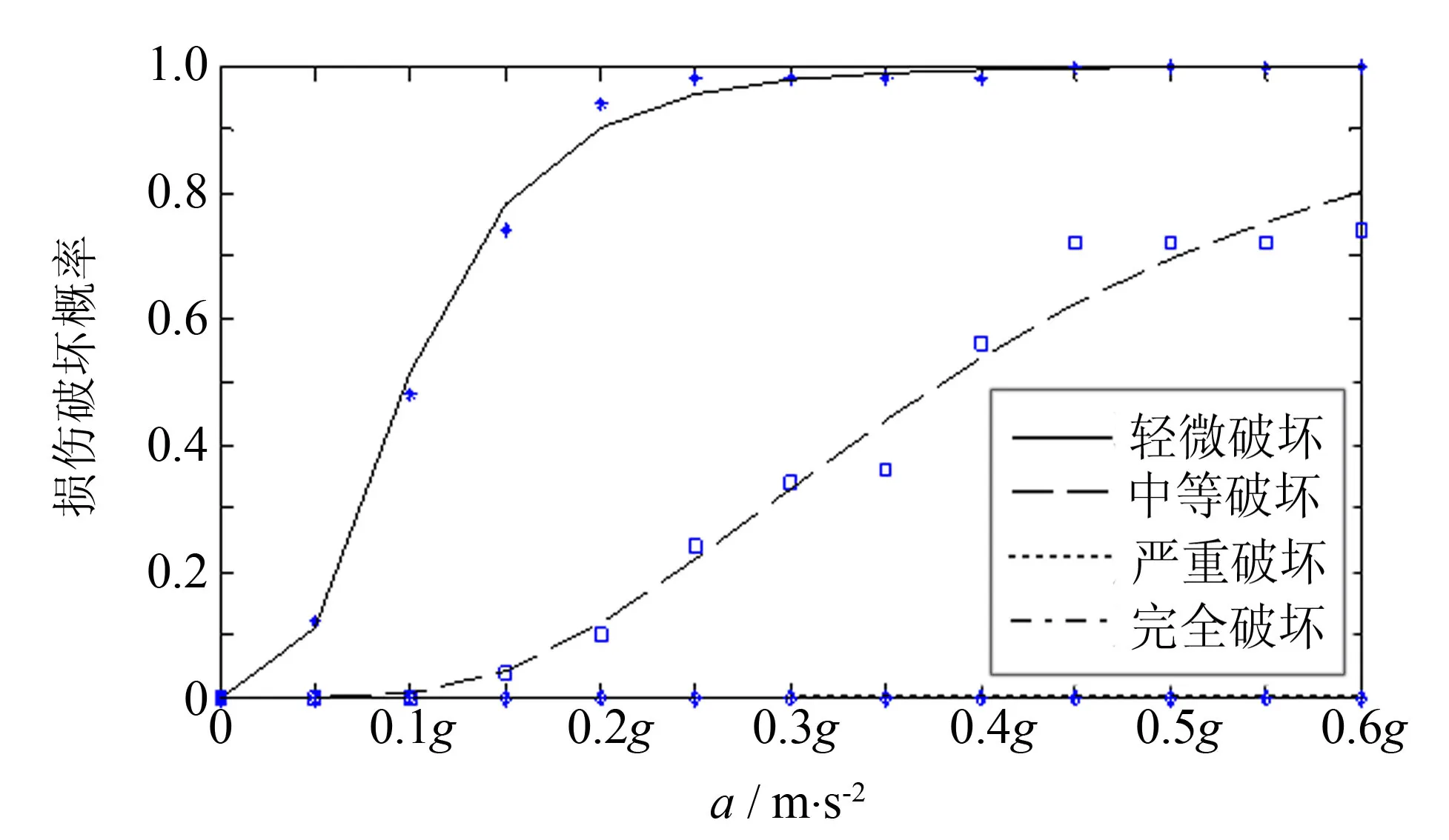
图10 支座易损性曲线图Fig.10 Fragility curve for the bearing

3.1.4 支座易损性曲线

对表10的损伤概率离散点进行回归拟合，可得到概率密度函数的拟合参数，根据拟合参数可以作出主梁的易损性曲线如图10示.左边墩支座的易损性高于右边墩支座的易损性，这是由于左边墩刚度大，支座与梁底或墩顶的接触面之间越容易滑动[8]，故以左边墩滑板支座的易损性曲线代表滑板支座的易损性曲线.由图10可以看出，在0.6g的地面运动下，滑板支座没出现严重和完全破坏，不会引起梁脱离支座或者落梁等形式的破坏，但是其轻微破坏的损伤概率大于墩和主梁.

3.1.5 斜拉索易损性曲线

对表11的损伤概率离散点进行回归拟合，可得到概率密度函数的拟合参数，根据拟合参数可以作出主梁的易损性曲线如图11示.六对斜拉索应力的增幅在100～400 MPa之间，总索力在900～1 250 MPa之间，外侧6号索的应力及变化幅度均最大，越靠近桥塔，索应力和应力增幅越小，故选取6号索的易损性曲线来表示斜拉索的易损性.斜拉索除了发生轻微破坏外，不发生其他损伤，安全储备较高.

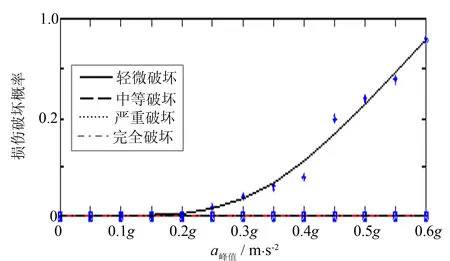
图11 斜拉索易损性曲线图Fig.11 Fragility curve for the cable

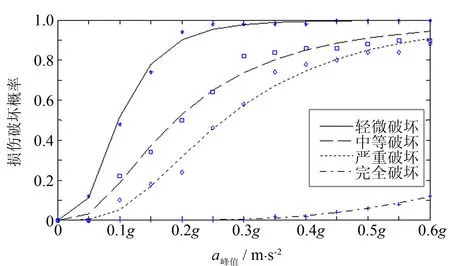
图12 全桥易损性曲线Fig.12 Fragility curve for the bridge

3.2 全桥易损性曲线

根据独塔部分斜拉桥各构件的损伤概率，采用第一顺序可靠度原则来确定全桥结构的易损性.选取各级地面运动作用下，各构件中损伤概率的最大值作为该级地面运动下的全桥结构地震易损性的损伤概率.由此可得全桥各级损伤概率，对损伤概率离散点进行回归拟合，可得概率密度函数拟合参数，根据拟合参数可得全桥易损性曲线如图12示.

4 结论

1)在0.05g～0.60g的顺桥向地面运动作用下，中墩是结构中最易破坏的构件，发生中等、严重和完全损伤破坏的概率最高.滑板支座是发生轻微破坏损伤概率最高的构件.针对这些构件采取相应的加固措施可使独塔斜拉桥在纵向地面运动作用下具有良好的抗震性能.

2)在0.05g～0.60g的顺桥向地面运动作用下，边墩不会出现完全破坏，其他等级的损伤概率都低于中墩；主梁损伤破坏概率比中墩、边墩的破坏概率低，但主梁进入弹塑性阶段，会使桥梁的刚度发生变化，影响墩、塔、支座、索等构件的损伤破坏；斜拉索仅发生轻微破坏，索应力最大值和最大增幅均出现在最外侧的索.桥塔、桩基的延性储备较高，处在弹性范围内.

3)本研究虽然提出了独塔部分斜拉桥的地震易损性曲线，但对结构能力随机性的假定、地面运动的选择、损伤指标的确定、全桥结构与构件损伤的联系等方面仍有提升的空间，可以进一步研究.

[1] 刘凯.曲线部分斜拉桥的几个设计参数研究[D].西安：长安大学，2013.

[2] 张菊辉.基于数值模拟的规则梁桥墩柱的地震易损性分析[D].上海：同济大学，2006.

[3] YANG C S W，WERNER S D，DESROCHESA R.Seismic fragility analysis of skewed bridges in the central southeastern United States[J].Engineering Structures,2014，83(1)：116-128.

[4] TAVARES D H，SUESCUN J R，PAULTRE P,etal.Seismic fragility of a highway bridge in quebec[J].Journal of Bridge Engineering，2013，18(11)：1 131-1 139.

[5] 吴少峰，上官萍.独塔部分斜拉桥顺桥向地震作用下主梁的易损性部位分析[J].福州大学学报(自然科学版)，2013，41(4)：550-555.

[6] 王义，张正伟，王龙辰.M法及非线性法在桩基础抗震设计中的对比研究[J].兰州工业学院学报，2014，2(21)：67-70.

[7] 谢旭.桥梁结构地震响应分析与抗震设计[M].北京：人民交通出版社，2006.

[8] 李枝军，葛飞，徐秀丽，等.板式橡胶支座性能有限元模拟与试验研究[J].东南大学学报(自然科学版)，2013，6(43)：1 299-1 303.

[9 ]PRIESTLEYM J N，SEIBLE F，CALVI G M.Seismic design and retrofit of bridge[M].New York：John Wiley and Sons，1997.

[10] 倪永军.桥梁结构抗震设计的设计地震与基于位移的抗震方法设计[D].北京：北方交通大学，2001.

[11] 中交路桥技术有限公司.公路工程抗震规范：JTG B02-2013[S].北京：人民交通出版社，2014.

[12] Federal Emergency Management Agency.Earthquake loss estimation methodology technical manua：HAZUS 99[S].Washington：[s.n.]，1999.

[13] MACKIE K,STOJADINOVIC B.Fragility curves for reinforced concrete highway overpass bridges[C]//The 13th World Conference on Earthquake Engineering.Vancouver:[s.n.],2004：1 553.

[14] HWANG H，LIU J B，CHIU Y H.Seismic fragility analysis of highway bridges[R].https://www.ideals.illinois.edu/bitstream/handle/2142/9267/Report01-06.pdf?sequence=2&isAllowed=y.

[15] 中华人民共和国交通部.公路桥梁板式橡胶支座：JT/T 4-2004[S].北京：人民交通出版社,2004.

[16] VAMVATSIKOS D,CORNELL C A.Incremental dynamic analysis[J].Earthquake Engineering and Structural Dynamics，2002，31：491-514.

[17] SHINOZUKA M，FENG M Q，LEE J，etal.Statistical analysis of fragility curves[J].ASCE Journal of Engineering Mechanics，2000，126(12):1 224-1 231.

[18] 交通运输部公路科学研究院.公路桥梁技术状况评定标准:JTG/T H21-2011[S].北京：人民交通出版社,2011.

(责任编辑：林晓)

Seismic fragility analysis on extra-dosed PC bridge with single-tower under the motion of longitudinal bridge direction

WU Shaofeng,SHANG-GUAN Ping，JIANG Shaofei

(College of Civil Engineering,Fuzhou University,Fuzhou,Fujian 350116,China)

The PC cable-stayed bridge with a single tower rigidly connected with the girder was selected as the object of the research.The dynamic increment method and data statistical analysis method were used to study the seismic vulnerability for bridge of this kind.The vulnerable elements and the corresponding damage probability were ensured under the ground motion in longitudinal bridge direction.The peak acceleration of ground motion was chosen as the intensity index input of the earthquake records with the use of vulnerability analysis theory and earthquake input was selected by the amplification coefficient.Damage status for each component was defined with the index of displacement ductility ratio,strength and deformation,relative displacement and the cable force.The vulnerability curve for the component and the whole bridge were established based on the damage probability.Results shows that the middle pier and the bearing were the most vulnerable part under the ground motion in longitudinal bridge direction,the side pier and the girder showed a damage at different degree and the cables,bridge tower and the piles showed a high safety storage.

extra-dosed PC bridge with single-tower；ground motion；seismic vulnerability; fragility curve; fullest damage extent

10.7631/issn.1000-2243.2017.02.0159

1000-2243(2017)02-0159-08

2015-12-10

吴少峰(1983-)，工程师，主要从事桥梁与结构工程研究，shaofeng45@163.com

国家“十二五”科技支撑计划资助项目(2015BAK14B02)，国家自然科学基金资助项目(51278127)

U448.27

A