土工格栅间距和凸点厚度对其界面特性试验的影响

唐晓松，王永甫，冯雨实

（1后勤工程学院军事土木工程系，重庆401331；2重庆市地质灾害防治工程技术研究中心，重庆400041；3重庆能源职业学院土木工程系，重庆402260）

土工格栅间距和凸点厚度对其界面特性试验的影响

唐晓松1,2，王永甫1,2，冯雨实3

（1后勤工程学院军事土木工程系，重庆401331；2重庆市地质灾害防治工程技术研究中心，重庆400041；3重庆能源职业学院土木工程系，重庆402260）

土工格栅因其能有效咬合或嵌固周围土体，改良土体的力学性能，且具有造价低廉等优点，因此在实际工程中得到了日益广泛的应用。目前，大都采用室内界面特性试验研究土工格栅的加筋机理，常用的有直剪摩擦特性试验和拉拔摩擦特性试验两种。由于仪器尺寸等试验条件的限制，现有的界面特性试验大都未考虑土工格栅竖向间距和其特有的凸点结构的影响，因此亟需寻求新方法。该文基于数值方法，分别研究了土工格栅的直剪摩擦特性和拉拔摩擦特性，分析了土工格栅竖向间距和凸点厚度对其界面特性的影响。研究表明，土工格栅的竖向间距较小，且凸点厚度较厚时，界面的强度指标较大，其加筋作用越强。因此，实际工程中应考虑土工格栅竖向间距和凸点厚度的影响，从而合理选择界面强度指标。

土工格栅；界面特性；数值方法；试验模拟；强度指标

土工格栅是土工合成材料的一种，其二维网格或具有一定厚度的三维立体网格能有效咬合或嵌固周围土体，从而改良土体的力学性能，因此土工格栅形成的加筋体结构，如：加筋土挡墙、加筋土边坡、加筋土地基等广泛应用于各类工程[1-4]。由于加筋体结构是加筋材料和其周围土体两种性质迥异的材料相互组合形成的，其共同作用机理十分复杂，其中尤以加筋材料界面特性的研究最为复杂，因此加筋体结构的设计理论远滞后于工程实践[5-6]。

目前，关于土工格栅界面特性的研究大都基于摩擦加筋理论，采用室内试验、模型试验和现场观测等方法[7-10]。其中，室内试验最为常见，主要有直剪摩擦特性试验和拉拔摩擦特性试验两种。关于两种常用的界面特性试验，大都仅根据土工格栅的网孔尺寸和土体颗粒的大小确定试验仪器的长和宽，且仅对直剪或拉拔界面处单层土工格栅的界面特性进行研究[11-13]，没有结合工程实际考虑土工格栅通常按一定竖向间距铺设，相邻土工格栅对界面处土工格栅界面特性可能会产生影响。同时，为了增强土工格栅的整体性，在纵横向土工格栅的连接处通常采用具有一定厚度和强度的凸点结构，以防止连接处剥离，目前关于凸点厚度对界面特性影响的研究也相对较少。

由此可以看出，由于仪器尺寸、试验方法等试验条件的限制，现有的土工格栅界面特性试验无法考虑土工格栅竖向间距和凸点厚度的影响，亟需寻求新思路和新方法。

1 土工格栅界面特性试验的数值模拟

国内外的研究表明，采用有限元法等数值方法研究土工格栅的界面特性是可行的[14-16]，因此文章采用荷兰PLAXIS B.V.公司开发的PLAXIS 3D有限元程序模拟土工格栅的界面特性试验。建立的数值模型中（如图1所示），上、下盒的几何尺寸为1000mm（长）×1000mm（宽）×900mm（高），土工格栅的竖向间距分别取300mm和600mm，通过在模型顶面设置面荷载模拟竖向加载，采用在上盒设置指定面位移模拟直剪摩擦特性试验；采用在上、下盒界面处的土工格栅前部施加指定面位移模拟拉拔摩擦特性试验。其中，土的基本物理力学性质指标取重度γ等于18kN/m3，粘聚力c土体等于1kPa，内摩擦角Φ土体等于30O。PLAXIS 3D程序采用界面单元基于弹塑性模型模拟土工格栅-土接触界面的相互作用，如图2所示。其中，土工格栅和土的界面抗剪强度指标取粘聚力c格栅-土体等于1kPa，内摩擦角Φ格栅-土体等于19.4O。采用板单元模拟土工格栅特有的凸点结构，其轴向杨氏模量取500kN/m2，剪切模量取192.3kN/m2，板单元厚度分别取2mm和5mm。土工格栅的轴向抗拉刚度取80kN/m，纵横向土工格栅条带宽15mm，网孔净尺寸为120mm×120mm，如图3所示。直剪试验时，土工格栅满铺长度1000mm；拉拔试验时，土工格栅长度770mm。

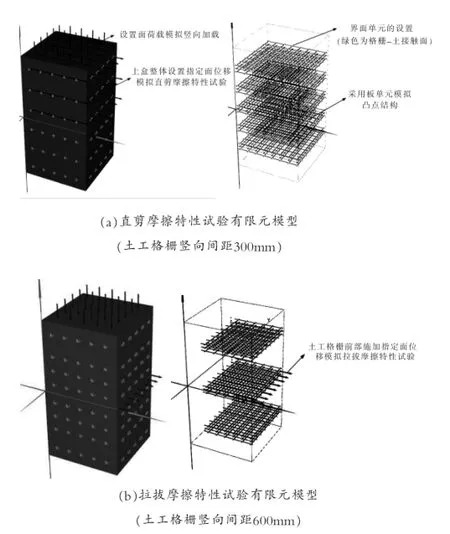
图1 有限元数值模型

图2 界面单元

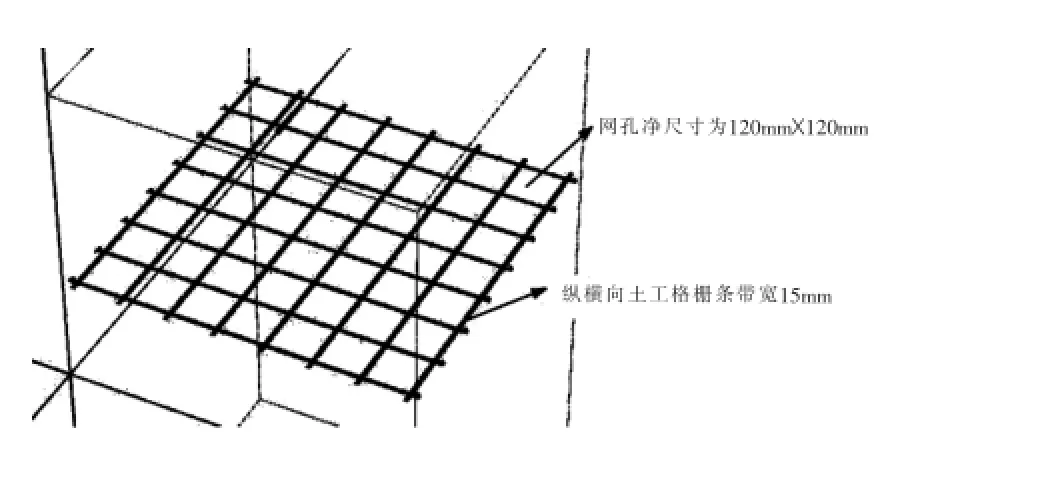
图3 土工格栅尺寸示意图

根据《公路工程土工合成材料试验规程》JTG E50-2006的相关要求[17]，在模拟直剪摩擦特性试验时上盒设置的指定面位移量应为剪切面长度的16.5%，即165mm；模拟拉拔摩擦特性试验时上、下盒界面处土工格栅前部施加的指定面位移为700mm。

通过数值计算可以得到的不同竖向荷载条件下界面合力和计算荷载步的关系曲线，根据其后部的近水平段，可以得到剪切或拉拔破坏时土工格栅整个界面上剪力的合力，如图4所示。通过计算界面上合力和对应的横截面面积的比值，可以得到不同竖向荷载条件下界面上的剪应力τ。以界面上剪应力τ为纵坐标，界面上正应力σ为横坐标。通过直线拟合，可以得到界面的强度指标c界面和Φ界面，从而定量研究土工格栅的界面特性。

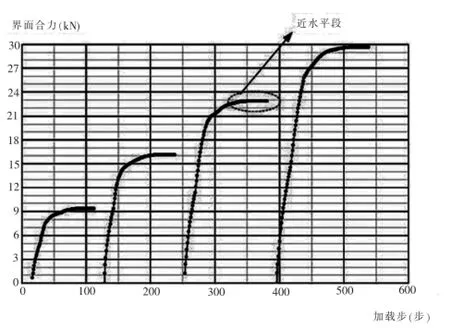
图4 各加载步界面剪力合力和荷载步关系曲线

2 基于数值方法的界面特性研究

2.1 土工格栅直剪摩擦特性的研究

分别在有限元模型的顶面设置50kPa、100kPa、150kPa和200kPa的竖向面荷载，指定上盒发生165mm的水平位移，计算得到不同竖向荷载条件下剪切破坏时界面上剪力的合力，如表1所示。

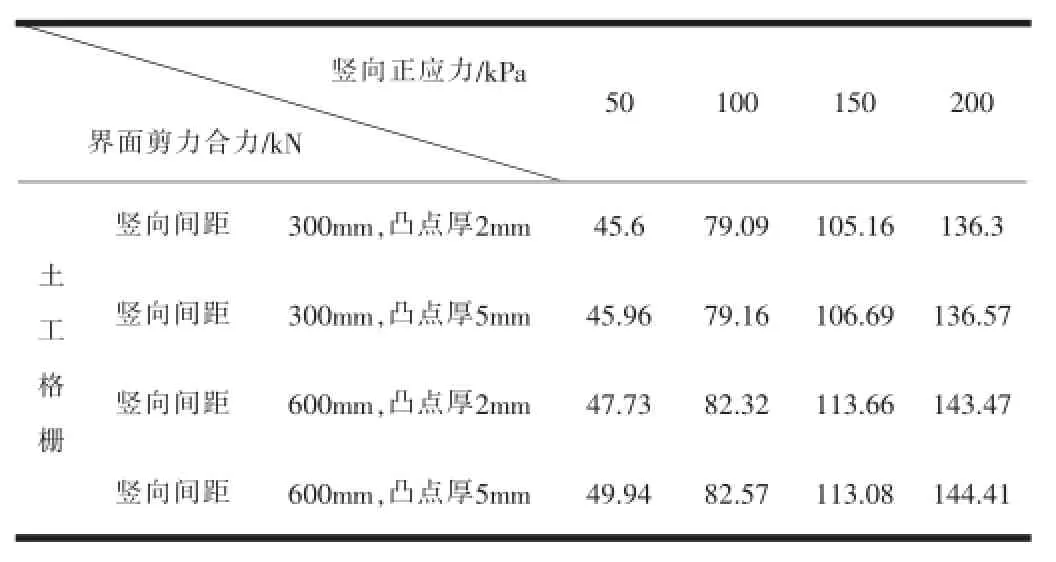
表1 剪切破坏时界面上的合力

由于剪切过程中界面处土工格栅的实际接触面积是递减的，为变值，因此每次计算界面剪应力时均应使用与最大剪切力出现时相应的实际接触面积值。以土工格栅竖向间距为300mm，凸点厚度为2mm，竖向荷载为50kPa时的计算结果为例，如图5所示。从图5（a）中可以看出，在第750荷载步以后，界面剪力合力和计算荷载步关系曲线出现峰值，取此时的峰值45.6kN作为界面剪力的合力。同时，根据上盒水平位移增量和计算荷载步的关系曲线（如图5（b）所示），对应界面剪力的合力出现峰值时，上盒的水平位移量为47mm，则此时界面实际接触面的长度为953mm，宽为1000mm，面积为0.953m2。因此，可以得到此时界面的剪应力τ为45.6/0.953=47.85kPa。按上述方法，不同竖向荷载条件下剪切破坏时界面上的剪应力的计算结果如表2所示。

图5 剪切破坏时界面有效接触面积的确定

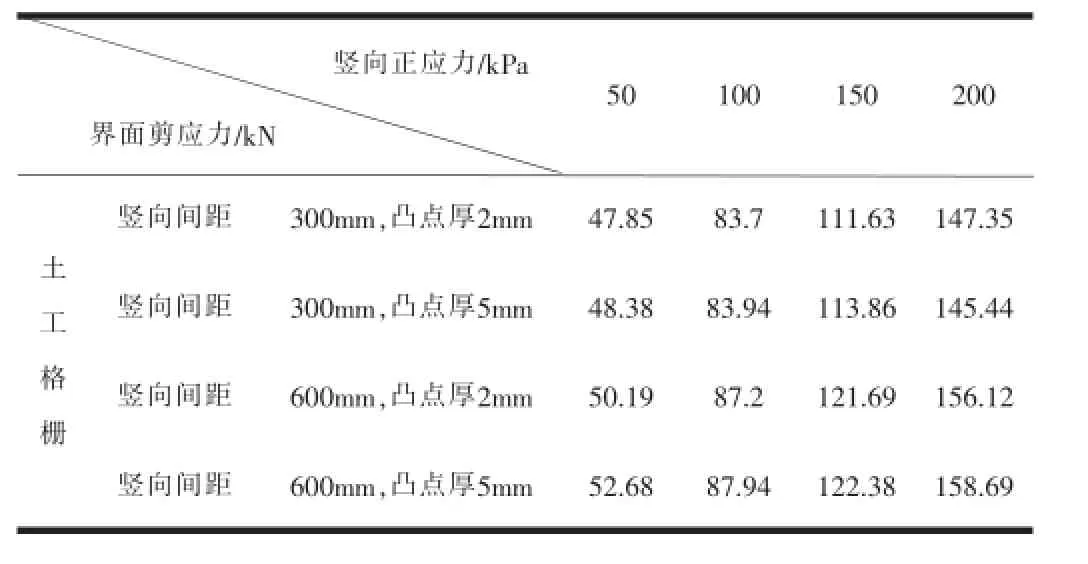
表2 剪切破坏时界面上的剪应力

对界面上正应力σ和界面上剪应力τ进行直线拟合，如图6所示。其中，直线线性公式的常数项即为界面粘聚力c界面，系数项即为界面内摩擦角Φ界面的正切值，这样就可以得到直剪条件下土工格栅界面的强度指标c界面和Φ界面，如表3所示。

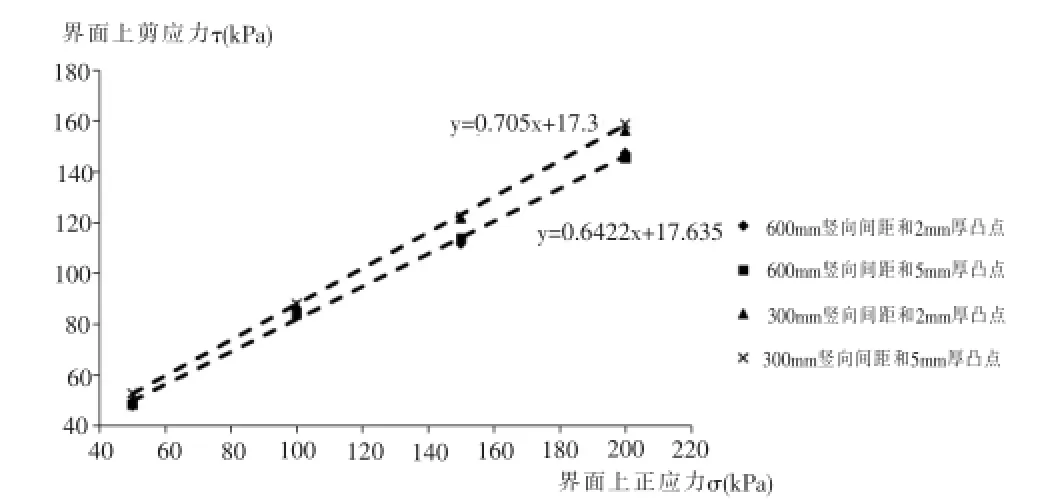
图6 界面正应力σ和界面剪应力τ的直线拟合（直剪摩擦特性试验）

表3 土工格栅界面的强度指标（直剪摩擦特性试验）

从计算结果可以看出，由于土工格栅和周围土体的相互作用，界面处的抗剪强度指标相比于土体的抗剪强度指标得到了明显提高。同时，土工格栅的竖向间距对界面直剪摩擦特性试验是有影响的，竖向间距越小，界面的抗剪强度指标相对越高，这主要是由于土工格栅和周围土体嵌固咬合在一起，形成一定的影响范围，因此当土工格栅竖向间距变小时，会对剪切面处土工格栅的界面特性产生一定的影响。另外，凸点结构厚度对界面直剪摩擦特性的影响不是很明显，相同竖向间距条件下，凸点厚度2mm和凸点厚度5mm对应的界面强度指标无明显变化。分析其原因主要是，直剪试验的剪切面相对固定，因此凸点结构的影响有限，如图7和图8所示，界面周围土体水平位移增量的等值线图基本一致。

图7 界面周围土体水平位移等值线图（竖向间距300mm，凸点厚2mm，竖向正应力200kPa）

图8 界面周围土体水平位移等值线图（竖向间距300mm，凸点厚5mm，竖向正应力200kPa）

2.2 土工格栅拉拔摩擦特性的研究

分别在有限元模型的顶面设置50kPa、100kPa和150kPa的竖向面荷载，且在上、下盒界面处土工格栅前部施加700mm指定面位移以模拟土工格栅界面的拉拔摩擦特性试验，如图1（b）所示。此时，拉拔界面土工格栅长770mm，相应的实际接触面面积为0.77m2。通过界面正应力σ和界面剪应力τ的直线拟合（如图9所示），可以得到拉拔条件下土工格栅界面的强度指标c界面和Φ界面，如表4所示。

图9 界面正应力σ和界面剪应力τ的直线拟合（拉拔摩擦特性试验）

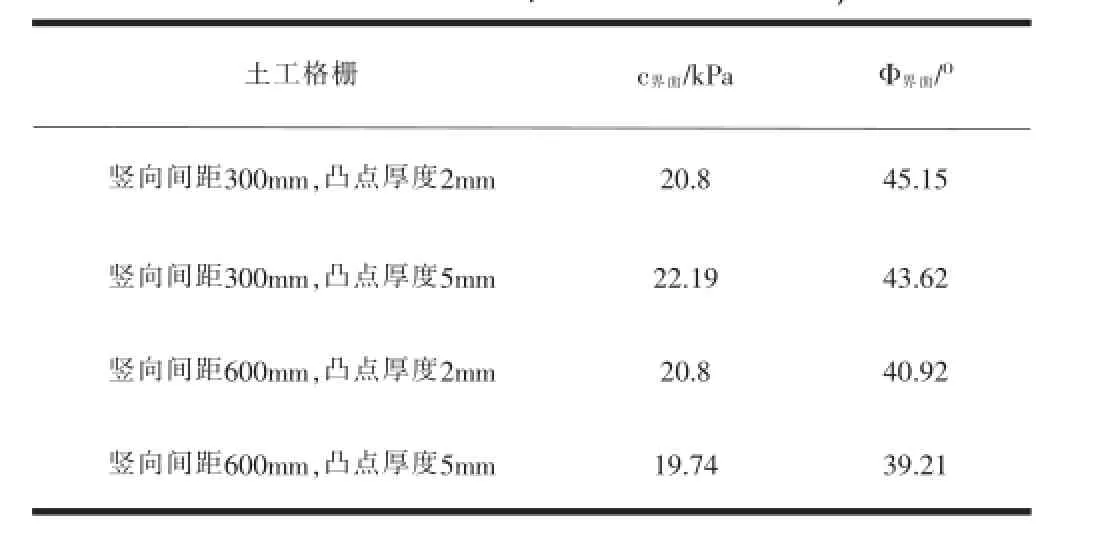
表4 土工格栅界面的强度指标（拉拔摩擦特性试验)

从表4中的计算结果可以看出，拉拔摩擦特性试验得到的界面强度指标均大于直剪摩擦特性试验得到的界面强度指标。分析其原因，主要是拉拔对周围土体的影响较直剪范围更大，因此其相对移动更为困难，相应的界面强度指标也更高。从图10-图13可以看出，土工格栅竖向间距越小，受土工格栅影响的土体范围越大；相同竖向间距条件下，凸点厚度越厚，土工格栅的影响范围也越大。因此，当土工格栅竖向间距较小，且凸点厚度较厚时，界面的强度指标较大。

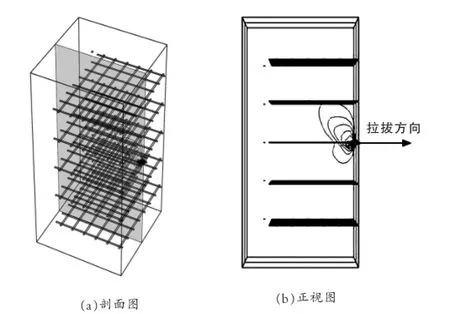
图10 界面周围土体水平位移等值线图（竖向间距300mm，凸点厚2mm，竖向正应力150kPa）

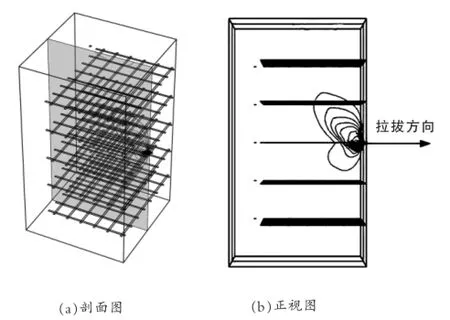
图11 界面周围土体水平位移等值线图（竖向间距300mm，凸点厚5mm，竖向正应力150kPa）

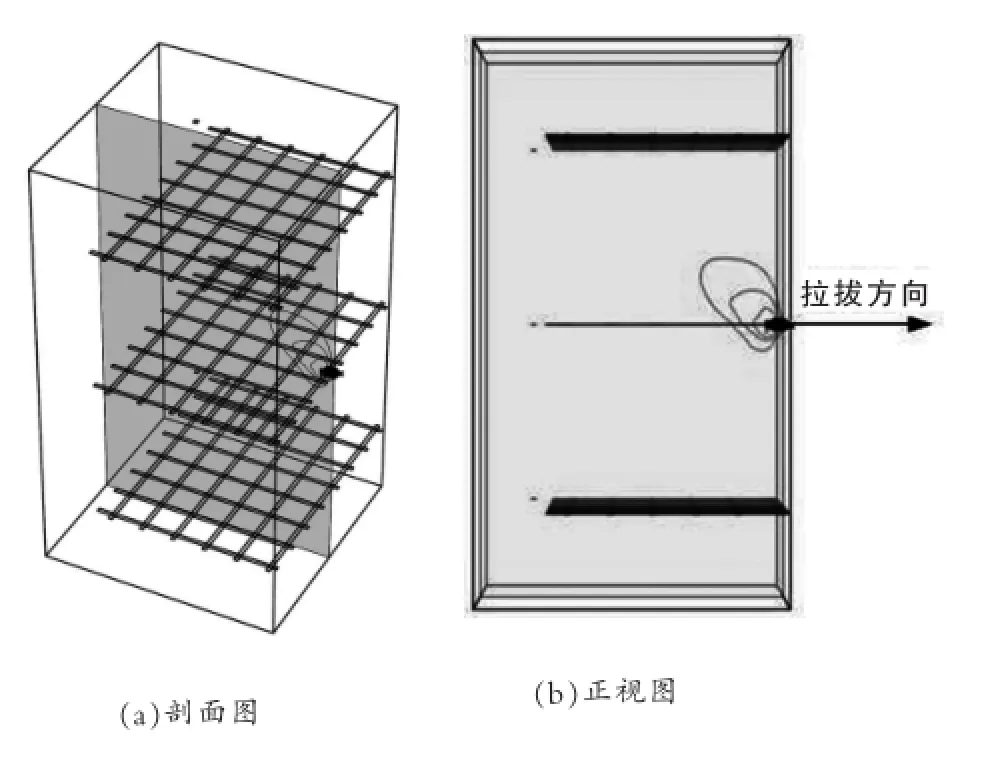
图12 界面周围土体水平位移等值线图（竖向间距600mm，凸点厚2mm，竖向正应力150kPa）

图13 界面周围土体水平位移等值线图（竖向间距600mm，凸点厚5mm，竖向正应力150kPa）

3 结论

通过文中的研究可以看出，基于数值方法能较好模拟土工格栅和土体之间的相互作用，从而定量且直观的研究土工格栅的界面特性，并得到如下结论：

（1）拉拔摩擦特性试验得到的界面强度指标均大于直剪摩擦特性试验得到的界面强度指标，分析其原因主要是拉拔土工格栅时对周围土体的影响范围更大，发生相对变形更困难。因此，实际工程中应根据土工格栅加筋体结构的破坏形式选择相应的界面参数，从而保证设计的合理性和可靠性；

（2）土工格栅的竖向间距不同，界面特性试验得到的界面参数也不同，因此界面特性试验的试验装置除了满足长度和宽度的要求，还应设计合理的仪器高度以考虑土工格栅间距的影响；

（3）采用板单元能够模拟土工格栅特有的凸点结构及其厚度对土工格栅界面特性的影响。从计算结果可以看出，凸点厚度从2mm变化至5mm，土工格栅对周围土体的咬合或嵌固作用也随之增强，土工格栅的加筋作用更优，且对土工格栅界面拉拔摩擦特性的影响更为明显。

[1]杨广庆.土工格栅加筋土结构理论及工程应用[M].北京：科学出版社，2010.

[2]M.Inanc Onur，Mustafa Tuncan，Burak Evirgen Bertan. Behavior of Soil Reinforcements in Slopes[J].Procedia Engineering，143（2016）：486-489.

[3]黄仙枝，白晓红.加筋带布置对地基承载力的影响[J].岩土力学与工程学报，2010，34（6）：1280-1283.

[4]唐晓松，郑颖人，王永甫.土工格栅加筋土挡墙在某机场滑坡治理工程中的应用[J].土木工程学报，2011，44（S2）：60-64.

[5]李广信，介玉新.土工合成材料加筋土边坡的设计方法[A]//2013第四届全国土工合成材料加筋土学术研讨会论文集[C]，2013，61-84.

[6]李广信.关于土工合成材料加筋设计的若干问题[J].岩土工程学报，2013，35（4）：605-610.

[7]张俊峰，王协群，邹维列.土-格栅界面强度参数和剪切刚度试验研究[J].长江科学院院报，2014，31（3）：77-83.

[8]王军，林旭，刘飞禹.砂土与格栅界面相互作用的直剪试验研究[J].岩土力学，2014，35（S1）：113-120.

[9]王家全，周岳富，陆梦梁.土工格栅拉拔试验及筋材受力特性分析[J].广西大学学报：自然科学版，2016，41（1）：134-140.

[10]郑俊杰，苗晨曦，谢明星.界面特性及填料粒径影响格栅加筋性能的离散元研究[J].岩土工程学报，2013，35（8）：1423-1428.

[11]Nicola Moraci，Piergiorgio Recalcati.Factors affecting the pullout behaviour of extruded geogrids embedded in a compacted granular soil[J].Geotextiles and Geomembranes，24（2006）：220-242.

[12]S.Balakrichnan，B.V.S.Viswanadham，Evaluation of tensile load-strain characteristics of geogrids through in-soil tensile tests[J].Geotextiles and Geomembranes，36（2016）：1-10.

[13]蔡剑韬.土工格栅加筋膨胀土拉拔试验研究[J].岩土力学，2015，36（S1）：203-307.

[14]M.Mosallanezhad，S.H.Sadat Taghavi，N.Hataf.Experimental and numerical studies of the performance of the new reinforecment system under pull-out conditions[J].Geotextiles and Geomembranes，44（2016）：70-80.

[15]M.S.Khedkar，J.N.Mandal.Pullout behaviour of cellular reinforcements[J].GeotextilesandGeomembranes，27（2009）：262-271.

[16]M.R.Abdi，A.R.Zandieh.Experimental and numerical analysis of large scale pull out tests conducted on clay reinforced with geogrids encapsulated with coarse material[J].Geotextiles and Geomembranes，42（2014）：494-504.

[17]中华人民共和国交通部.JTG E50-2006公路工程土工合成材料试验规程[S].北京：人民交通出版社，2006.

责任编辑：孙苏，李红

Influence of Geogrids Distance and Thickness of Salient Points on Interface Property Experiment

Geogrid has been growingly used because of its effective embedding with the surrounding soil,the mechanic property improvement for soil and low cost.At present,indoor experiments of interface property are conducted to study the reinforcement mechanism of geogrid,including direct shear friction experiment and pullout friction experiment.Due to the limitation of facility sizes and other experimental conditions,the influences of the vertical distances between geogrids and its peculiar salient points are hardly considered in most of current experiments,so some new method should be worked out.Based on numerical methods,this paper respectively studies the features of direct shear friction and pullout friction of geogrids and analyzes the influences of vertical distances between geogrids and the thickness of salient points on the interface property.The research shows that the strength indexes of interface are relatively larger and the functions of reinforcement are stronger when the vertical distances between geogrids are smaller and the thickness of salient points are larger.In practical engineering,the influence of vertical distances of geogrids and the thickness of salient points should be considered to choose reasonable strength indexes for the interface.

geogrids;interface property;numerical method;experimental simulation;strength index

TU599

A

1671-9107（2017）04-0035-05

基金论文：该论文为“重庆市教委科学技术研究项目（项目编号：KJ1754490)土工格栅摩擦加筋机理及其工程应用”的研究论文之一。

10.3969／j.issn.1671-9107.2017.04.035

2017-02-16

唐晓松（1979-），男，江苏海门人，博士，高级工程师，主要从事岩土工程稳定性分析及其数值模拟研究。