基于BP神经网络的变量喷雾供药系统研究
2017-04-24张敏范龙代祥肖静徐幼林
张敏,范龙,代祥,肖静,徐幼林
(南京林业大学机械电子工程学院,南京210037)
基于BP神经网络的变量喷雾供药系统研究
张敏,范龙,代祥,肖静,徐幼林*
(南京林业大学机械电子工程学院,南京210037)
在变量喷雾供药系统的研究中,由于控制对象及控制算法尚未突破,使得目前的精确供药系统很难满足动态变化的变喷量精确农药流量控制。笔者从变量喷雾供药系统入手,基于流量调节阀的开度及其两端压差决定其通流量大小的原理,对变量施药的供药系统进行了研究,利用Matlab中的BP神经网络工具箱函数对试验结果进行了拟合和测试,结果表明:流量调节阀两端压差恒定时,其通流量的大小与其开口度存在一定的正相关关系;利用BP神经网络拟合了压差恒定时,通流量与调节阀开度的非线性递增关系曲线,经过结果分析,验证了BP神经网络在该控制系统中的可行性。此项试验分析为变量喷雾精确供药的深入研究提供了理论基础。
变量施药;供药系统;流量调节阀;开口度;BP神经网络
我国是粮食生产大国,同样也是农作物病虫害发生比较严重且频繁的国家,因此,化学农药的施用利于有效控制病虫害,为提高农业产量做出了巨大贡献[1-2]。我国是农药生产和使用大国,但农药的有效利用率仅为30%左右,而发达国家却高达60%~70%[3-4]。农药使用量大、效率低,造成环境污染、人员中毒、残留超标等诸多负面问题,影响我国粮食的绿色安全[5-6]。为了提高农药使用率,减少对环境的污染,国内开展了一系列农药精确施用方法的研究[7-9],这在提高施药装备技术水平的同时,还可以解决制约中国化学防治病虫害推广应用中的有关“瓶颈”问题[10-11]。
随着人们对农药残留、环境污染和农药有效利用率越来越重视,变量施药已成为精确农药使用技术研究的一个重要发展方向[12]。实行变量施药技术,可以使单位面积的施药量根据作物自身以及具体的病虫害状况实时调整,使实际施药量与需求值相一致[13-14],从而能够达到高产、优质、环保和经济的目的。目前,变量施药技术需在如下方面寻求突破:可变量精确施药系统及其控制方式,如美国MICRO-TRAK公司研究生产了MT系列自动变量控制系统[15],邱白晶等[16]研制了一种基于3S技术的变量施药装置;另一个是作物信息动态采集及其对靶施方式,如史岩等[17]研制了基于CCD图像采集处理技术的自动对靶压力式变量施药系统。但总体来说,动态的作物信息、特别是深度信息的采集问题,以及施药系统控制对象及其自动控制系统的响应延时问题、变量施药引起供药系统压力突变所导致的流量不稳定问题,还有满足定量、精确施药的控制算法问题等,都使变量施药技术在精量适时施药或处方施药技术等方面与市场要求存在较大差距。
影响施药系统单位面积施药量的因素很多,其中供药控制系统中电动调节阀对流量特性的影响最为明显。为解决变量施药时,供药系统压力突变所引起的流量不稳定问题,笔者针对变量供药控制系统,研究实时调整电动调节阀的开口度精确控制系统中的供药量方法,同时拟利用神经网络算法设计控制系统,旨在提高农药利用率,减少化学物质对农业生态环境的污染。
1 材料与方法
1.1 试验材料
选用型号为ZRHP-16C的电动调节阀,通过调节阀实现不同大小的开口度来调节流回药箱的流量,改变变量施药系统的供药量,电动调节阀的特征参数见表1;选用型号为LWGY-15的涡轮流量计,用来采集供药系统的药液流量,其特征参数见表1;采用型号为BJZ15的不锈钢射流式自吸泵作为液压循环系统的动力,其特征参数见表2。

表1 电动调节阀和涡轮流量计特征参数

表2 BJZ15不锈钢射流式自吸泵的特征参数
1.2 试验系统与试验方法
调节阀的流量特性包括理论流量特性和实际流量特性。理论流量特性指调节阀前后压差不变时所获得的流量特性,它取决于阀芯的形状。实际应用的时候,调节阀安装在管道系统上,它两端的压差是变化的,流量调节阀的流通量表达式[18]为:
(1)
式中:Q为调节阀通流量,m3/s;ρ为流体密度,g/cm3;Kv为流量系数;P1和P2分别为阀上游和阀下游的压力,MPa;N为工程单位系数。
上式可以改写为:
Q=KvAΔPm
(2)
式中:Kv表示调节阀孔口系数;A表示调节阀孔面积(即孔径大小),cm3;ΔP表示调节阀在管道系统两端的压差,MPa;m表示压差指数。
从公式(2)可以看出,流量调节阀的内部通流量与其两端压差ΔP以及孔口形状系数Kv有关。由于调节阀孔口为圆形,当改变孔口大小时,其形状随之变化,导致Kv(孔口形状系数)值发生变化,因此,在压差不变的情况下,流过调节阀的流量大小主要取决于调节阀的开口度。故在流量调节阀两端压力差恒定的情况下,通流量与调节阀开口度关系的表达式为:
Q=f(O)
(3)
式中:O为阀门开度。
鉴于金融开放与经济增长之间关系的不确定性,很多学者尝试探究其影响因素。相关影响因素主要有制度质量和宏观条件、资本流动,汇率波动等。Klein发现一国制度因素和金融机构质量影响资本账户开放与经济增长之间的互动关系[7]。Bussiere et al发现从中长期看,制度质量和资本流入构成是金融开放促进经济增长的重要因素[8]。荣晨、董瞾以资本积累率分析资本账户开放与经济增长的关系[9]。李丽玲、王曦将汇率波动的作用引入资本账户开放和经济增长的关系中,发现控制汇率的波动可以促进资本账户开放收益[10]。
为了研究调节阀的流动特性与孔径大小,管道系统两端压差存在的具体关系,设计如图1所示的试验系统进行测试。
整个试验系统由射流式自吸泵、溢流阀、涡轮流量计、压力表、电动调节阀、调压阀、药箱等按如图1a所示连接成一个供药控制系统。射流式自吸泵将药水输送到系统中;根据其额定流量,调节溢流阀使泵的出口压力恒定保持在0.3 MPa;涡轮流量计实时显示回路中的流量大小;支路节流调节与主路调节类似,但原理相反。主要区别在于支路节流调节中,流量调节阀是以溢流的方式调节系统流量变化的。当药水经过流量调节阀时,通过研发的自动控制系统调节阀的开口度,改变通流面积,从而改变其通流量的大小,达到控制系统出口流量的目的,而回路中多余的流量将通过溢流阀溢出。为了模拟植物形态发生动态变化时所带来的喷头开启数的动态变化,试验系统采用通过调整调压阀的出口流量,以模拟喷头启闭数变化所产生的流量变化。
研究过程中采用先调节流量调节阀的开口度,然后根据流量调节阀两侧压力表测量的压力值,通过溢流阀手动调节使其压差达到目标值0.3 MPa的试验方法,研究电动调节阀开度大小对其通流量特性的影响。根据设计试验系统原理,将准备的试验设备连接成如图1b所示的试验系统实物图。

图1 电动调节阀流动特性测试系统Fig. 1 Schematic diagram and experimental system set-up for measuring flow characters of motorized valve
2 结果与分析
2.1 试验数据结果
通过上述试验系统可测出在电动调节阀两端压力为0.3 MPa时,不同电动调节阀开口度对应通流量的大小。由于电动调节阀的最大开口度为15 mm,测量精度为0.01 mm,故将0~15 mm电动调节阀的开口度分为100级,每级开口度为0.15 mm进行试验,具体数据散点图如图2所示。
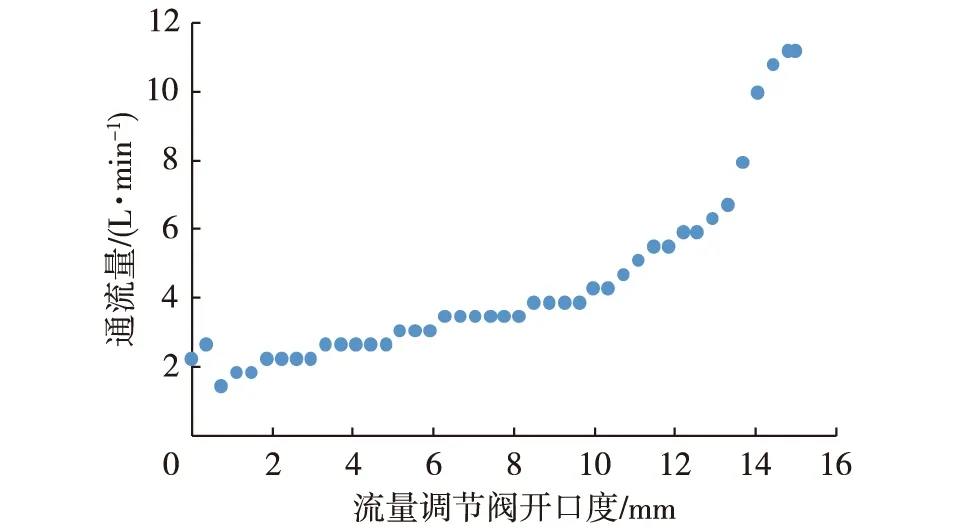
图2 开度对应通流量的原始数据Fig. 2 The original data of opening size degree and the flux
由散点图可以看出,当调节阀闭合时,通流量为0 L/min,所以测得的前两个点存在误差,可以去掉,散点趋势先平缓上升,再急剧上升,存在这样的变化趋势是因为调节阀阀口的形状影响了Kv的大小。同时,随着电动调节阀开口度的不断增大,通流量有增大的趋势,可以看出两者之间存在一种非线性关系,但散点图无法表示出这种非线性关系。为了深入了解数据中存在的规律,即在控制系统中,电动调节阀的开度大小与其通流量的大小之间的具体非线性关系,本研究采用Matlab中的BP神经网络对这种非线性关系进行拟合分析。
2.2 BP神经网络训练结果分析
2.2.1 样本输入与模型训练
为了确定电动调节阀开度与其通流量的精确非线性关系,需要确定合适的网络结构,本研究采用3层神经网络结构进行建模,输入量为流量值,输出量为电动调节阀的开度值。3层神经网络的数学表达式可表示为:
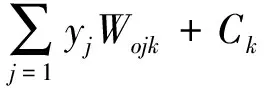
(4)

(5)
BP神经网络传输函数主要有非线性Sigmoid函数和线性Purelin函数。用于模式识别时,BP神经网络隐层采用Sigmoid函数,输出层采用Purelin函数。当BP神经网络的输入层到隐含层采用Sigmoid函数的双曲正切Tansig作为传输函数时,网络的误差比采用对数函数Logsig[19]小,所以BP神经网络的神经元传递函数采用S型正切函数Tansig,输出层神经元传递函数采用线性函数Purelin。训练函数参数设置如下:迭代次数为100,网络训练学习率为0.01,误差性能目标值0.000 4。
根据神经网络结构和传递函数及参数,采用0.3 MPa下,前34组不同阀径对应的流量的大小为输入样本数据,对神经网络模型进行训练仿真,用最后8组数据进行测试检验。对输入样本数据使用Matlab中的mapminmax函数进行归一化处理以消除量纲影响,提高网络收敛性能,使用newff函数构建神经网络,调用trainlm函数利用Levenberg Marquardt算法训练网络。训练结束后,获取输入层至隐层的对应权值矩阵,隐层输出的对应权值矩阵以及输入和输出层的各个对应阈值(表3)。

表3 BP神经网络各层权值和阈值
网络训练结束利用测试数据预测此训练模型,对仿真结果使用postmnmx函数进行反归一化处理,得到BP神经网络模型的准确率。
2.2.2 BP神经网络测试及结果分析
训练结果见图3。图3a是神经网络训练的整体结构,包括网络框架、使用算法及训练的进度过程;图3b为网络性能,均方误差收敛于0.207 2,小于目标值,说明网络性能较好;图3c中网络训练梯度呈良好的下降趋势且收敛,验证次数为零,说明验证过程中输出误差一直减小;图3d为样本实际输出与目标输出的拟合程度,拟合程度较高。BP神经网络对此训练的非线性关系测试后,电动调节阀开度大小的预测与实际输出结果见表4。

图3 电动调节阀开度对其通流量大小影响的BP神经网络训练结果Fig. 3 BP neural network training results of the influence of the opening size of motorized valve on the flux

测试组输入数据/(m3·h-1)理论输出/mm实际输出/mm差值(理论-实际)35035512562512135404271360355129375130170-00795370403133125137365-04240380477136875142144-05269390599140625142271-01646400648144375142272021034106721481251422720540342067215000014227207728
在Matlab中,提供的mse函数计算输出变量与期望变量之间的均方误差,求得perf=0.207 2,误差较小,说明了利用BP神经系统拟合的非线性关系是正确的,并证明了供药系统中电动调节阀流量的大小与其开度的大小存在非线性递增关系。
3 结 论
本研究首先测试了供药系统电动调节阀的通流量与其开度的数据,然后通过BP神经网络拟合其中的非线性关系,得到了如下结论:
1)针对变量供药控制系统,研究完成了通过实时调整电动调节阀的开口度,实现精确控制系统中的供药量方法,并搭建了试验系统,试验表明该系统能够实现可变量供药。
2)利用试验系统,采集了调节阀开口度与流通量的关系数据,并利用神经网络对数据进行了网络建模和训练,在此基础上对系统输出进行预测,通过分析预测结果与实际结果,得出实际变量与期望变量之间的均方误差为0.207 2,误差在允许范围内,表明BP神经网络算法在本研究的变量供药控制系统中的可行性。
3)将BP神经网络算法用于供药系统的无级变量控制,避免了采用模糊控制算法分级控制流量所带来的流量输出不精确的弊端,使得农药流量的智能控制更加适宜于在针对动态变化植物作业时的可变量精确供药系统。
[1]张小超, 胡小安, 任继平, 等. 精准农业关键技术与装备的研究进展[C]//2005年中国农业工程学会学术年会论文集, 2005.
[2]徐赛章. 我国植保机械现状与展望[J]. 农村机械化, 1997(3):9-11.
[3]王锦江, 陈志, 杨学军. 基于AT89C51单片机的变量施药控制系统研究[J]. 农机化研究, 2007(11):147-149. WANG J J, CHEN Z, YANG X J. Study on controlling system based on AT89C51 single-chip microcomputer for variable spraying[J]. Journal of Agricultural Mechanization Research, 2007(11):147-149.
[4]杨学军, 严荷荣, 徐赛章, 等. 植保机械的研究现状及发展趋势[J]. 农业机械学报, 2002, 33(6):129-131, 137. YANG X J, YAN H R, XU S Z, et al. Current situation and development trend of equipment for crop protection[J]. Transactions of the Chinese Society of Agricultural Machinery, 2002, 33(6):129-131, 137.
[5]PANNETON B, THÉRIAULT R, LACASSE B. Efficacy evaluati on of a new spray-recovery sprayer for orchards[J]. Transactions of the ASAE, 2001, 44(3):473-479.
[6]TUMBO S D, SALYANI M, WHITNEY J D, et al. Investigation of laser and ultrasonic ranging sensors for measurements of citrus canopy volume[J]. Applied Engineering in Agriculture, 2002, 18(3):367-372.
[7]SVENSSON S A, FOX R D, HANSSON P A. Forces on apple trees sprayed with a cross-flow fan air jet[J]. Transactions of the ASAE, 2002, 45(4):889-895.
[8]MILLER D R, SALYANI M, HISCOX A B. Remote measurement of spray drift from orchard sprayers using LIDAR[C]//2003 ASAE Annual Meeting. American Society of Agricultural and Biological Engineers, 2003:1.
[9]陈勇, 郑加强. 精确施药可变量喷雾控制系统的研究[J]. 农业工程学报, 2005, 21(5):69-72. CHEN Y, ZHENG J Q. Control system for precision pesticide application based on variable rate technology[J]. Transactions of the Chinese Society of Agricultural Engineering, 2005, 21(5):69-72.
[10]傅泽田, 祁力钧, 王俊红. 精准施药技术研究进展与对策[J]. 农业机械学报, 2007, 38(1):189-192. FU Z T, QI L J, WANG J H. Developmental tendency and strategies of precision pesticide application techniques[J]. Transactions of the Chinese Society for Agricultural Machinery, 2007, 38(1):189-192.
[11]卢秉福, 张祖立, 朱明, 等. 农业机械化发展关键影响因素的辨识与分析[J]. 农业工程学报, 2008, 24(11):114-117. LU B F, ZHANG Z L, ZHU M, et al. Discrimination and analysis of key influencing factors for agricultural mechanization development[J]. Transactions of the Chinese Society of Agricultural Engineering, 2008, 24(11):114-117.
[12]王锦江, 孙星, 严荷荣, 等. 注入式变量施药控制系统设计[J]. 农机化研究, 2013, 35(9):129-132. WANG J J, SUN X, YAN H R, et al. Control system design of injective variable rate spraying[J]. Journal of Agricultural Mechanization Research, 2013, 35(9):129-132.
[13]玄子玉, 张玉峰, 田思庆. 车载喷雾机变量施药控制系统的设计[J]. 农机化研究, 2012, 34(5):116-119. XUAN Z Y, ZHANG Y F, TIAN S Q. Design of controlling system for variable rate spraying based on microcontroller[J]. Journal of Agricultural Mechanization Research, 2012, 34(5):116-119.
[14]随顺涛. 车载式变量施药机控制系统研究[D]. 杨凌:西北农林科技大学, 2009. SUI S T. Study on control system of variable rate sprayer hauled by tractor[D]. Yangling:Northwest A&F University, 2009.
[15]胡开群, 周舟, 祁力钧, 等. 直注式变量喷雾机设计与喷雾性能试验[J]. 农业机械学报, 2010, 41(6):70-74, 102. HU K Q, ZHOU Z, QI L J, et al. Spraying performance of the direct injection variable-rate sprayer[J]. Transactions of the Chinese Society for Agricultural Machinery, 2010, 41(6):70-74, 102.
[16]邱白晶, 李会芳, 吴春笃, 等. 变量喷雾装备及关键技术的探讨[J]. 江苏大学学报(自然科学版), 2004, 25(2):97-101. QIU B J, LI H F, WU C D, et al. On variable-rate spraying equipment and its key technology[J]. Journal of Jiangsu University(Natural Science Edition), 2004, 25(2):97-101.
[17]史岩, 祁力钧, 傅泽田, 等. 压力式变量喷雾系统建模与仿真[J]. 农业工程学报, 2004, 20(5):118-121. SHI Y, QI L J, FU Z T, et al. Model development and simulation of variable rate of pressure spray[J]. Transactions of the Chinese Society of Agricultural Engineering, 2004, 20(5):118-121.
[18]李晋阳, 贾卫东, 魏新华. 基于流量调节阀和神经网络的植保机械在线混药装置[J]. 农业机械学报, 2014, 45(11):98-103. LI J Y, JIA W D, WEI X H. On-line mixing pesticide device based on flow control valve and neural network[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(11):98-103.
[19]蒲春, 孙政顺, 赵世敏. Matlab神经网络工具箱BP算法比较[J]. 计算机仿真, 2006, 23(5):142-144. PU C, SUN Z S, ZHAO S M. Comparison of BP algorithms in Matlab NN toolbox[J]. Computer Simulation, 2006, 23(5):142-144.
Study on the pesticide-delivery system of variable-ratespraying based on BP neural network
ZHANG Min, FAN Long, DAI Xiang, XIAO Jing, XU Youlin*
(College of Mechanical and Electronic Engineering, Nanjing Forestry University, Nanjing 210037, China)
In the research on the pesticide-delivery system of the variable-rate spraying, the current accurate pesticide-delivery system is difficult to meet the dynamic change of the variable-rate spraying for the accurate pesticide flow regulating because of limitations in the control variable and its control algorithm. The accurate pesticide flow control of the variable-rate spraying can reduce the environmental pollution caused by excessive pesticides as well as the damage of the pesticide residue for human and animals, and improve the efficiency of the pesticide application. An experimental investigation was conducted for the pesticide-delivery system of the variable-rate spraying based on the mechanism of the flux of the flow determined by the opening size of a flow regulating valve and the pressure difference between both ends. According to the specific influence of regulator on flux flow, the correlation between them was analyzed through choosing the appropriate experimental device such as: flow control valve, pressure gauge and turbine flow meter. The pesticide-delivery system of the variable-rate spraying was designed by building the test bench and implementing the theoretical ideas into practice. The BP neural network toolbox of Matlab was used to simulate the test results. The results showed that in the pesticide-delivery system of the variable-rate spraying, there is a certain positive correlation between the flow flux and the opening size of the flow regulating valve. The increasing nonlinear relationship between them was simulated by BP neural network under the constant pressure difference. The application feasibility of BP neural network in the regulating system was tested and verified, which can avoid the disadvantages of inaccurate flow output caused by the hierarchical fuzzy control algorithm and can make the intelligent control of pesticide flow more suitable for the dynamic change of the variable precision pesticide-delivery system in plant protection operations. The results of this study will provide theoretical basis for the further research on the accurate pesticide-delivery system of the variable-rate spraying.
variable-rate pesticide application; pesticide-delivery system; flow regulating valve; opening size; BP neural network
2016-04-28
2016-11-29
江苏省农机三新工程项目(NJ2014-11);江苏省农业科技支撑计划项目(BE2012383);江苏高校优势学科建设工程资助项目(PAPD);2013年度江苏高校优秀科技创新团队(苏教科[2013]10号)。
张敏,女,研究方向为农林植保机械。通信作者:徐幼林,女,教授。E-mail:youlinxu@njfu.edu.cn
TP183
A
2096-1359(2017)02-0133-05
