杉木目测等级规格材足尺抗压和拉伸强度的设计值研究

龚迎春，王朝辉，江京辉，骆秀琴，任海青

(中国林业科学研究院木材工业研究所，北京100091)

杉木目测等级规格材足尺抗压和拉伸强度的设计值研究

龚迎春，王朝辉，江京辉，骆秀琴，任海青*

(中国林业科学研究院木材工业研究所，北京100091)

杉木具有生长周期快、力学性能好、耐腐性强等优点，被广泛应用于工程木产品的制备，如规格材、胶合木和木基复合材料。但是由于缺少设计值，其在建筑结构领域的使用存在安全隐患。先根据加拿大NLGA分等规则，将杉木规格材分为SS(structural select)、No.1和 No.2 三个等级，再根据ASTM D4761-02和ASTM D198-02分别进行足尺的抗压和拉伸测试，选取正态分布和对数分布对测试数据进行拟合，利用K-S检验对正态分布和对数分布进行拟合优度检验。参照木材容许应力法和ASTM D2915-03计算杉木规格材设计值。结果表明：No.1等级规格材在15%含水率条件下的抗压和拉伸强度最小，其主要缺陷为节子，对力学性能影响较大；No.2等级规格材主要缺陷为钝棱，对强度影响不大。SS等级规格材的抗压和拉伸测试数据与对数分布拟合效果更优；No.2等级规格材的抗压和拉伸测试数据与正态分布拟合效果更佳。SS、No.1和No.2等级规格材抗压强度参考设计值分别为11.50，11.33和11.05 MPa，拉伸强度参考设计值分别为8.95，8.15和7.18 MPa。

杉木；目测等级；规格材；足尺测试；抗压强度；拉伸强度；设计值

发展绿色木质建材，是我国实现节能减排、社会可持续发展战略目标的重要举措[1-2]。2015年9月，工信部和住建部联合出台的《促进绿色建材生产和应用行动方案》，首次明确提出大力推广木结构产业[3]。政策的扶持必将极大地促进木结构建筑在我国的发展。我国第八次森林资源清查结果显示，我国人工林种植面积居世界第一，人工林面积已增加到0.69亿hm2，蓄积量增加到24.83亿m3[4]。杉木(Cunninghamialanceolata)是我国主要的三大人工林树种之一，具有生产周期快、材质优良和分布区域广等特点，主要应用于屋架、搁栅和门窗等[5-6]。轻型木结构是建筑应用中木材利用率和预制化程度最高的集成体系，但是杉木应用到现代轻型木结构中还缺乏相当多的基础数据，其中最重要的是强度设计值指标。

我国木材强度设计值主要是根据无疵小试样测算，其强度的概率分布采用正态分布。但无疵小试样不能体现木材的天然缺陷，如节子、钝棱和斜纹理等，不能完全准确地反应木材本身的强度变异性特征，强度的数据并不完全符合正态分布[7-8]，目前国际上普遍采用足尺测试来计算不同等级规格材的设计值。笔者采用加拿大NLGA法对杉木进行目测分等，NLGA目测等级SS(structural select)、No.1和 No.2与我国GB 50005—2003《木结构设计规范》规定的规格材目测等级Ic、IIc和IIIc相对应，参照ASTM D4761-02和ASTM D198-02标准分别进行足尺的抗压和拉伸测试，对强度测试数据采用正态分布和对数分布进行概率分布拟合；参照木材容许应力法和ASTM D2915-03标准计算杉木规格材的设计值，以期对杉木在现代木结构上的应用提供理论依据。

1 材料与方法

1.1 试验材料

杉木购自安徽黄山林场、四川洪雅县和龙林场、湖南雪峰山林场和福建省将乐县光明国有林场，其中，安徽、四川、湖南的杉木用于顺纹抗压性能测试，福建的杉木用于顺纹拉伸性能测试。各林场杉木的平均树龄、胸径和树高见表1。选用312根3 m长的原木段，采用四面下锯法锯解[9]，得到尺寸为45 mm×90 mm×2 550 mm的规格材。随机选取部分规格材作为抗压和拉伸试样，测试时足尺试样的含水率约为12%。根据NLGA分等规则，将规格材分为SS、No.1和 No.2 三个等级。不同等级抗压和拉伸试件的尺寸和样本数见表2。

表1 不同林场杉木的基本信息

表2 不同等级试件尺寸和样本数

1.2 试验方法

参照ASTM D4761-02进行抗压测试，从每个规格材上截取2个试件，其中一块必须包含最大的强度降等缺陷，另一块必须包含次要的强度降等缺陷，最终的抗压强度取较小值。抗压测试设备为岛津万能力学试验机，加载速率为2 mm/min。顺纹拉伸强度参照ASTM D198-02进行测试，拉伸测试设备为Metriguard Model 412型拉伸试验机，加载速率为2 mm/min。抗压和拉伸试件破坏后，在破坏区域附近截取试样，参照GB/T 1931—1991测定规格材含水率。抗压和拉伸强度计算公式如下：

σ=Fmax/(bt)

(1)

式中：σ为抗压(拉伸)最终极限强度；Fmax为最大破坏载荷，N；b和t分别为试件宽度和厚度，mm。

1.3 含水率调整

参照ASTM D1990标准，将抗压和拉伸强度试件含水率调整到15%以下，如公式(2)所示：

(2)

式中：M1为测试时的含水率，%；UCS和UTS分别为测试时的抗压和拉伸强度，MPa。

1.4 概率分布模型

在分析材料的力学性能时，通常采用正态分布和对数分布模型对测试数据进行拟合。正态分布模型是统计学中最常用的模型，但由于其对称性以及均匀变动，往往与实测结果不符。因此，笔者引入偏正态分布的对数分布模型。分布函数f(x)和累积分布函数φ(x)如下:

1)正态分布

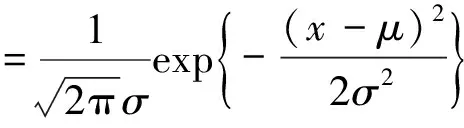
(3)

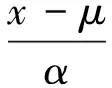
(4)

式中：x为随机变量；μ和σ分别为平均值和标准偏差；p为累积分布函数的百分位值。

2)对数分布

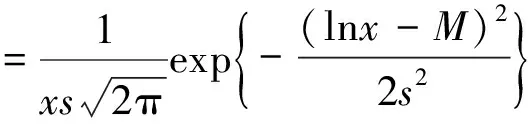
(5)

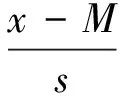
(6)

式中：M为lnx的平均值；s为lnx的标准偏差。

1.5 K-S(Kolmogorov-Smirnov)检验

K-S检验可以被用来对分布曲线进行拟合优度检验[10]，检验公式如下：

D=max(|φ(x)-s(x)|)

(7)

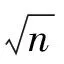
2 结果与分析

2.1 抗压和拉伸强度测试结果

不同等级杉木最终极限抗压和拉伸强度见表3。SS等级规格材的抗压和拉伸强度最大分别为30.71和28.57 MPa，而No.1等级规格材的抗压和拉伸强度最小。这是因为No.1等级规格材的主要缺陷为节子，节子对力学性能的影响很大[11]；No.2等级规格材的主要缺陷为节子和钝棱，但节子的数量相对较少，对强度的影响不大[12-13]。抗压和拉伸强度的变异系数变化范围为13.55%～24.22%。Green等[14]研究表明，规格材抗压强度的变异系数变化范围为10.70%～31.80%，与本研究的抗压强度变异系数范围一致。

表3 杉木规格材的抗压和拉伸强度

2.2 抗压和拉抻强度的概率分布

抗压和拉伸强度的直方图、正态分布和对数分布曲线见图1。从直方图中可以看出，SS等级规格材抗压强度数据在右侧更集中，No.1和No.2等级规格材的抗压强度数据更加符合正态分布。SS和No.1等级规格材的拉伸强度呈现偏正态分布，数据集中在左侧。正态分布和对数分布的统计参数见表4。

表4 正态分布和对数分布的统计参数

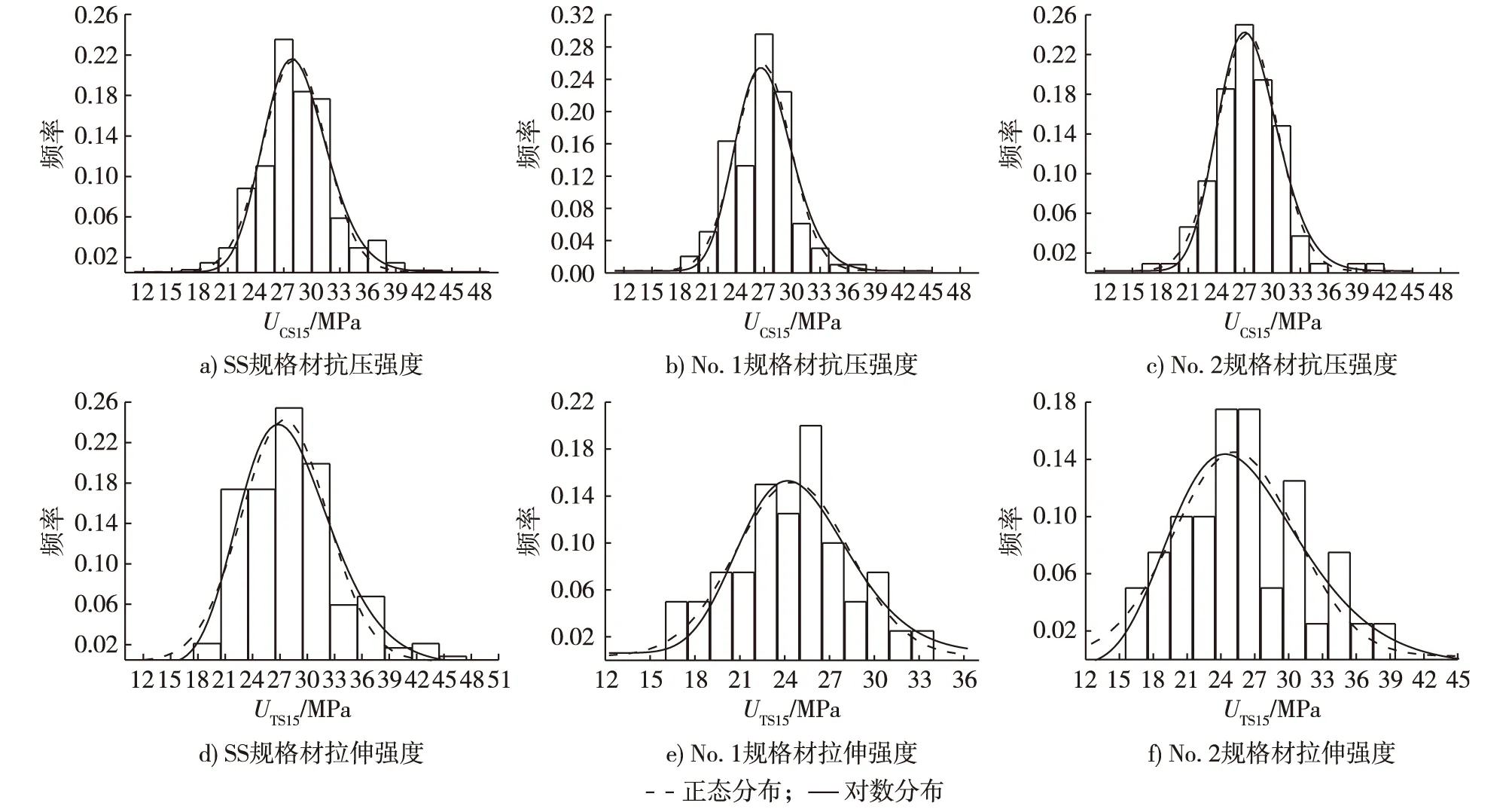
图1 不同等级规格材抗压和拉伸强度的概率分布曲线Fig. 1 Probability distribution curves of compressive and tensile strength for different grades dimension lumbers

K-S检验结果见表5，不同的测试样本数对应不同临界D值。不同等级规格材的抗压和拉伸强度分布模型的D值均小于在0.05显著水平上的临界值D0.05，说明正态分布和对数分布均能拟合测试数据。SS等级规格材的抗压强度对数分布的D值小于正态分布的D值，说明对数分布能更好地拟合SS等级规格材的抗压强度测试数据，在直方图中反映出来SS等级规格材抗压强度数据偏右集中。而No.1和No.2等级规格材抗压强度结果则表明，正态分布能更好地拟合抗压强度的测试数据。SS和No.1等级的拉伸强度对数分布D值小于正态分布的D值，说明对数分布拟合测试数据更佳。木材的强度与木材缺陷有密切关系，对足尺试件进行强度测试能更好地反映实际情况，需要根据不同的数据类型选取最佳的拟合分布曲线[15]。

表5 抗压和拉伸强度的K-S检验结果

2.3 特征值和设计值

为更安全地评估强度指标，比较不同分布类型的强度特征值，本研究采用正态分布和对数分布计算杉木规格材的特征值。特征值是指符合规定质量的锯材性能概率分布的某一分位值，抗压和拉伸强度特征值取统计分布具有75%置信度的5%分位值。参照GB 50068—2001《建筑结构可靠度设计统一标准》和ASTM D2915-03计算杉木规格材的特征值，服从对数分布，特征值计算公式如下：

f=eμf(1-kδf)

(8)

式中：μf为抗压和拉伸强度对数平均值；δf为抗压和拉伸强度对数分布变异系数；k为特征系数，在GB 50068—2001中k=1.645，在ASTM D2915中，在75%置信度和5%分位值的下限条件下，不同的样本数对应的k值不同(抗压强度：SS等级的k值为1.739，No.1和No.2等级的k值为1.758。拉伸强度：SS等级的k值为1.714，No.1和No.2等级的k值为1.834)。

服从正态分布，特征值计算公式如下：

f=μf-ks

(9)

式中：s为抗压和拉伸强度的标准偏差；k为特征系数。

不同等级杉木规格材拉伸和抗压强度的特征值见表6。根据对数分布计算的抗压和拉伸强度特征值基本都大于根据正态分布计算的特征值，除了No.2等级规格材抗压强度的特征值；根据GB 50068—2001计算所得特征值大于根据ASTM D2915-03计算所得特征值。对于不同等级规格材，抗压和拉伸强度特征值由大到小依次为SS>No.1>No.2。考虑到杉木在实际工程中的使用安全，本研究根据正态分布的特征值(f3和f4)计算杉木规格材的设计值。

表6 不同等级杉木规格材抗压和拉伸强度特征值

根据木材容许应力法[16]计算杉木规格材的设计值。由于本研究采用足尺试件测试，试件本身包含木材天然缺陷和干燥缺陷，因此在强度折减时不考虑上述两种缺陷的影响，计算公式如下：

f3d=f3k1k2/(k3k4)

(10)

式中：f3为特征值(表6)，k1为长期荷载系数，k2为应力集中系数，k3为超载系数，k4为结构偏差系数。

杉木构件的折减系数[15]见表7。根据 ASTM D2915-03计算杉木规格材的设计值，计算公式如下：

f4d=f4/K

(11)

式中：f4为特征值(表6)，K为折减系数(抗压强度的折减系数为1.9；拉伸强度的折减系数为2.1)。

设计值计算结果见表8。

表7 杉木构件应力折减系数

表8 不同等级杉木规格材抗压和拉伸强度设计值

由表8可知，考虑在工程应用中的安全可靠性，本研究选用木材容许应力法[16]计算设计值。除了No.1和No.2等级的拉伸强度，根据木材容许应力法计算所得设计值基本都小于采用ASTM D2915-03计算所得设计值。因此，安徽、湖南及四川采伐的杉木不同等级规格材足尺抗压强度的参考设计值分别为11.50(SS等级)，11.33 (No.1等级)和11.05 MPa(No.2等级)；在福建采伐的杉木足尺拉伸强度的参考设计值分别为8.95(SS等级)，8.15(No.1等级)和7.18 MPa(No.2等级)。设计值的确定为杉木在建筑结构领域的应用提供了理论依据。材料强度设计值也可采用极限状态设计方法求得，与木材容许应力法有较大的相似之处。极限状态设计法是以概率理论为基础，用可靠度指标度量结构构件的可靠度，后续增加测试样本数，可用极限状态设计法计算杉木规格材设计值。

3 结 论

1)No.1等级杉木规格材抗压和拉伸强度最小，分别为28.38和24.49 MPa，No.1等级规格材主要缺陷为节子，对力学性能影响较大；No.2等级规格材主要缺陷为节子和钝棱，但节子的数量相对较少，对强度的影响不大。

2)对3个等级规格材的抗压和拉伸强度数据进行概率分布拟合，不同等级规格材的最佳拟合分布曲线不同，需要根据不同的数据类型选择最佳的拟合分布曲线。SS等级的抗压和拉伸测试数据与对数分布拟合效果更优；No.2等级的抗压和拉伸测试数据与正态分布拟合效果更佳。

3)通过试验测得了杉木规格材的主要力学性能，并给出了参考设计值。考虑到杉木在实际工程中使用时的安全，在安徽、湖南及四川采伐的杉木规格材足尺抗压强度参考设计值为11.50(SS等级)，11.33(No.1等级)和11.05 MPa(No.2等级)；在福建采伐的杉木规格材足尺拉伸强度的参考设计值为8.95(SS等级)，8.15(No.1等级)和7.18 MPa(No.2等级)。

[1]娄万里, 任海青. 木结构建筑的特征及在我国的发展前景[J]. 木材工业, 2015, 29(5)：20-23. LOU W L, REN H Q. Characteristics and prospects of wood structure building in China[J]. China Wood Industry, 2015, 29(5)：20-23.

[2]周海宾, 任海青, 吕建雄, 等. 杉木目测等级规格材抗拉强度长度尺寸效应[J]. 建筑材料学报, 2010, 13(5)：646-649. ZHOU H B, REN H Q, LYU J X, et al. Size effect of length on tensile strength of visually-graded Chinese fir dimension lumber[J]. Journal of Building Materials, 2010, 13(5)：646-649.

[3]龚迎春, 任海青. 正交胶合木的特性及发展前景[J]. 世界林业研究, 2016, 29(3)：71-74. GONG Y C, REN H Q. Characteristics and development prospect of cross-laminated timber[J]. World Forestry Research, 2016, 29(3)：71-74.

[4]徐济德. 我国第八次森林资源清查结果及分析[J]. 林业经济, 2014(3)：6-8. XU J D. The 8th forest resources inventory results and analysis in China[J]. Forestry Economics, 2014(3)：6-8.

[5]任海青, 黄安民, 刘君良, 等. 杉木加工利用研究进展及建议[J]. 木材工业, 2006, 20(1)：25-27. REN H Q, HUANG A M, LIU J L, et al. Research on and suggestions for processing and utilization of Chinese fir[J]. China Wood Industry, 2006, 20(1)：25-27.

[6]郭伟, 任海青, 殷亚方. 杉木目测分等规格材缺陷类型及分布的研究[J]. 建筑材料学报, 2009, 12(4)：462-465. GUO W, REN H Q, YIN Y F. Study on types and distribution of visual characteristics about Chinese fir dimension lumbers[J]. Journal of Building Materials, 2009, 12(4)：462-465.

[7]赵秀, 关帅, 崔宇佳, 等. 结果用规格材抗压强度的概率分布[J]. 林业科技, 2013, 38(4)：41-44. ZHAO X, GUAN S, CUI Y J, et al. Probability distributions of ultra compression strength for the dimension lumber of larch [J]. Forestry Science & Technology, 2013, 38(4)：41-44.

[8]ZHUANG X J. Reliability study of North American dimension lumber in the Chinese timber structures design code[D]. University of British Columbia, 2004.

[9]周永东, 叶克林. 下锯法对落叶松规格材出材率及质量的影响[J]. 木材工业, 2009, 23(2)：1-3. ZHOU Y D, YE K L. Effects of sawing methods on dimensional lumber recovery and quality[J]. China Wood Industry, 2009, 23(2)：1-3.

[10]KOLMOGOROV A. Sulla determinazione emppirica di unalegge di istribuzione[J]. Giorn Ist Ital Attuar, 1993, 41(1): 83-91.

[11]谢力生, 刘佳权, 乔鹭婷. 节子对落叶松胶合木胶合性能的影响[J]. 林业工程学报, 2016, 1(1)：21-24. XIE L S, LIU J Q, QIAO L T. Influence of kont on the agglutination properties of Chinese larch glulam[J]. Journal of Forestry Engineering, 2016, 1(1)：21-24.

[12]郭伟, 任海青, 费本华, 等. 杉木人工林3个目测等级规格材的力学性质[J]. 林业科学, 2011, 47(11)：139-143. GUO W, REN H Q, FEI B H, et al. Mechanical properties of three grades of Chinese fir dimension lumber[J]. Scientia Silvae Sinicae, 2011, 47(11)：139-143.

[13]龙超, 吕建雄. 规格材强度性能测试方法的研究进展[J]. 木材工业, 2007, 21(5)：1-4. LONG C, LYU J X. Progress on the testing methods for mechanical properties of dimensional lumber[J]. China Wood Industry, 2007, 21(5)：1-4.

[14]GREEN D W, ROSALES A N. Properties and grading of Danto and Ramon 2 by 4’s[J]. Forest Products Journal, 2006, 56(4)：19-25.

[15]GONG Y C, ZHANG C Q, ZHAO R J, et al. Experimental study on tensile and compressive strength of bamboo scrimber[J]. BioResources, 2016, 11(3)：7334-7344.

[16]肖岩, 杨瑞珍, 单波, 等. 结构用胶合竹力学性能试验研究[J]. 建筑结构学报, 2012, 33(11)：150-157. XIAO Y, YANG R Z, SHAN B, et al. Experimental research on mechanical properties of glubam[J]. Journal of Building Structures, 2012, 33(11)：150-157.

Design values of compressive and tensile strength for visuallygraded Chinese fir dimension lumber

GONG Yingchun, WANG Zhaohui, JIANG Jinghui, LUO Xiuqin, REN Haiqing*

(Research Institute of Wood Industry, Chinese Academy of Forestry, Beijing 100091, China)

Being widely used for dimension lumber, glued lumber and wood-based composites, Chinese fir has the advantages of fast-growing, good mechanical performance and decay resistance. However, the application in the building structures was limited due to the lack of design values of mechanical properties. To utilize the green building material, this study aimed at obtaining the design values of Chinese fir for the building structures. The dimension lumbers for Chinese fir were divided into structural select (SS), No.1 and No.2 grades according to the NLGA Standard of Canada. The compressive strength and tensile strength of specimens were full-size tested according to ASTM D4761-02 and ASTM D198-02, respectively. The normal and lognormal distributions were selected to fit the experimental data. The K-S testing was used to estimate goodness of fit for normal and lognormal distributions. The design value was calculated according to Chinese allowable stress design method and ASTM D2915-03. The results showed that theUCS15(compressive strength under 15% moisture content) andUTS15(tensile strength under 15% moisture content) of No.1 grade lumber were lower than that of other lumber grades due to the great influence of knots. Besides, No.1 grade lumber contained more knots. In addition, the wane and skips in No.2 grade lumber had no significant effect on the wood strength. The experimental data of compressive and tensile strength for SS grade lumber fitted better by using the lognormal distribution. Conversely, the normal distribution fitted No.2 grade lumber better than the lognormal distribution did. The calculated design values ofUCSwere 11.50, 11.33 and 11.05 MPa for SS, No.1 and No.2 grade lumber, respectively. The calculated design values ofUTSwere 8.95, 8.15 and 7.18 MPa for SS, No.1 and No.2 grade lumber, respectively.

Chinese fir; visually grade; dimension lumber; full-size test; compressive strength; tensile strength; design values

2016-09-13

2016-11-01

中央级公益性科研院所基本科研业务费专项资金(CAFYBB2016ZX002)。

龚迎春，男，研究方向为木材力学与木结构。通信作者：任海青，女，研究员。E-mail:renhq@caf.ac.cn

S781.2

A

2096-1359(2017)02-0022-06