砂带虚拟形貌的建模*

何喆 李建勇,2 刘月明,2 聂蒙,2 樊文刚,2

(1.北京交通大学 机械与电子控制工程学院， 北京 100044;2.北京交通大学 载运工具先进制造与测控技术教育部重点实验室， 北京 100044)

砂带磨削是磨削加工的一种方式，可以看作众多植于基材表面的微切削刃与工件相互作用的过程.砂带的磨削性能不仅取决于磨削时施加的工艺参数，还与砂带表面形貌特征息息相关.所谓形貌特征是指砂带表面磨粒形状、尺寸、排布间距以及出刃高度等信息.在砂带的制造流程中，形貌特征由制造方法决定，本身带有极强的随机性，难以定量描述.这导致在加工过程中无法确定实际参与磨削的动态切刃数目及所处的切削状态，从而深刻影响加工表面质量、磨削力、磨削温度等方面的研究[1- 2]，阻碍砂带磨削技术的发展.

随着计算机技术的发展，虚拟磨削技术得到了普及[3]，建立磨具的虚拟形貌成为解决上述问题的新思路.因此，众多学者围绕磨具虚拟形貌模型的建立开展了丰富的研究工作.目前对磨具虚拟形貌建模主要以砂轮为主，可细分为两种方式[4]：其一为从微观磨粒入手，研究磨粒形状、尺寸与排布规律，生成磨具虚拟表面.Pellegrin等[5]将磨粒等效为随机多面体，该多面体为多个平面依据特定规则切割坯料而成.在一定程度上，它表征了磨粒的形状特征，用以研究磨削过程中磨粒的锋利程度；Hisakado等[6]将磨粒的形状简化为半球体或尖顶圆锥，研究了两种模型下工件与磨具之间的摩擦因数.在磨粒分布规律方面，刘月明等[7]将随机值多次赋予互不干涉的磨粒，获得磨粒的空间位置；张祥雷等[8]划分互不干涉的区块，将磨粒随机放置于各个区块内，进而获得磨粒的随机位置.其二为统计磨具表面特征，建立多参量函数拟合磨具表面.曹有为等[9]通过对砂轮表面的采样与数据处理，运用统计学理论和Johnson变换方法获得了非正态分布砂轮表面形貌的数学描述方程；吕长飞等[10]假设磨粒高度为非高斯随机分布，采用Johnson变换和Gabor小波变换在随机域内对砂轮表面形貌进行了仿真.

必须指出的是，砂带与砂轮制造方式与各自磨粒形状的不同导致砂带与砂轮虚拟形貌之间存在较大差异[11].有学者[12- 13]在开展形貌角度定量描述磨具属性或量化磨具磨损程度的工作中，因两者形貌不同而区别对待.文中所阐述的砂带虚拟形貌建模方法将采用随机多面体构建砂带磨粒的基本特征，设定相应的磨粒排布算法，将众多磨粒随机排布于砂带基材表面，从而建立砂带的虚拟形貌.利用统计方法获得实际砂带表面的相关参量，对比虚拟表面与实际表面的相关参量，验证砂带虚拟形貌模型的合理性与模型建立方法的正确性.

1 砂带磨粒多面体模型

实际砂带磨粒是大块磨料经辊式破碎机碾压破碎而成.破碎后微小磨粒长宽比近似为3∶1[11].在对磨粒进行分类时，通常经过两道筛网进行筛选.磨粒直径分布介于两次筛网孔径之间即为同一粒度.因此，同粒度磨粒的直径为一特定范围.Hou与Chen等[14- 15]经研究后认为，同一粒度的磨粒直径服从正态分布.设磨粒的直径为dg，其分布规律为

(1)

为保证砂带磨粒具有特定的长宽比，采用随机多面体方式建立磨粒三维模型.首先建立三轴比例为1∶1∶3的椭球体内核(两短轴长为dg，长轴长为3dg)，并将椭球体内核内接于一立方体.过椭球体表面任意一点做其外切面并与立方体相交.多次重复建立切面，将切面与立方体包络而成的几何体作为砂带单颗磨粒形状.图1所示为不同切面数目下模型磨粒与实际磨粒的形状对比.

图1 不同切面磨粒模型与真实磨粒对比

Fig.1 Comparison of grain model and real grain in various sections

磨粒形状建模是砂带虚拟形貌建模的最小单位，其运算量直接决定了砂带虚拟形貌的复杂程度.单颗磨粒形状建模的过程中，存在着最佳磨粒切面数目选取的问题.过少的切面数目会造成模型对真实磨粒描述存在偏差，而过多的切面数目会使单颗磨粒形状过于复杂，增加砂带虚拟形貌建立过程中无意义的计算量.借助文献[16]中所阐述的磨粒几何参数计算方法，选取磨粒刀尖角作为判别标准，按随机多面体方式建立不同切面数目模型，24、36粒度磨粒各12颗，测量各个磨粒在不同切面数目下的刀尖角均值，将结果汇总于图2.

图2不同切面数目下的刀尖角Fig.2 Sharp angles in various sections

分析图2可知，磨粒三维模型在较少切面时其刀尖角与实际值相差较大，三维多面体模型不能准确描述实际磨粒的几何特征.随着构建磨粒模型的切面数目增加，磨粒的刀尖角愈发接近实测值.在切面数目为24至30时，三维模型的刀尖角与真实磨粒刀尖角相对误差小于7%.当切面数目超过30时(如36与42切面)，刀尖角的大小出现了波动.为达到计算量与磨粒准确描述的平衡点，最佳切面数目约为24至30.

砂带制造过程中，通常采用静电植砂技术将砂带磨粒均布于基材之上.由于磨粒尖端的静电荷积累现象，磨粒大都以刃尖朝外的方式附着于基材上.现设计相应的数值仿真算法模拟磨粒在基材表面的分布情况，以达到与实际砂带类似的磨粒分布情况.

2 砂带磨粒分布规律

为准确获得磨粒在砂带表面的分布情况，采用由美国Nanovea公司生产的表面轮廓仪(PS50 profiler)对砂带表面进行采样测量(图3).该设备由测量笔、移动平台及数据处理器组成.测量笔能够在100～1 000 Hz的可变采样频率下，以非接触式测量方式沿z方向获得精度为0.4 μm、量程在3 mm内的数据信息，而移动平台可以容纳最大为50 mm×50 mm的测量样本以8 μm的移动精度在Oxy平面内平移.根据本实验中测量尺度，设备满足精度需求.

图3 表面轮廓仪组成Fig.3 Surface profiler composition

2.1 磨粒辨识

研究磨粒的分布规则应首先辨识出砂带表面上的磨粒.磨粒通过粘结剂牢固附着于砂带表面，其尖部明显突出于粘结剂表面，在磨削过程中作为微小切削刃对工件材料进行切除.由于砂带磨粒尖端通常为多峰结构，为避免磨粒的重复计数，宜采取适当的采样间隔对砂带表面进行采样测量.Blunt等[17]指出，适当的采样间隔δ为

(2)

图4(a)为采用适当的采样间隔，通过表面轮廓仪获得的砂带高度伪色图，由于磨粒尖端远高于砂带粘结剂表面，可通过两者高度差异分离出磨粒，进而确定其所在的位置.依据Darafon等[18]所阐述的Blob算法，提取伪色图中高度较高部分，获得如图4(b)所示的砂带磨粒在伪色图中磨粒的分布情况.实验中采集了36粒度陶瓷氧化铝砂带与24粒度绿碳化硅砂带10 mm×10 mm的随机样本各5个，统计采样区域内磨粒数目均值，结果如表1所示.根据磨粒直径的经验公式(1)，磨粒粒度号越大其直径越小，则采样区域内所能容纳的磨粒数量越多.

图4 砂带表面相关信息的提取Fig.4 Processing information of abrasive belt surface

粒度磨粒材料磨粒平均直径/mm采样尺寸/(mm×mm)采样间隔/μm磨粒数目/个平均间距/mm36氧化铝陶瓷0.4510×10120272.2024绿碳化硅0.7910×10250183.13

2.2 磨粒平均间距

磨粒在砂带表面随机分布，其间距是表面形貌仿真的关键因素.按图4(b)所示，采用Blob算法后，在采样区域内选定长为l、宽为w的计数区域，以Gi(i=1,2,3,…,n)为标记对n颗磨粒进行编号.将磨粒所占据区域的包络圆圆心作为磨粒的所在位置，以Gi(xi,ji)为标记获得各个磨粒位置，则任意两个磨粒间距离sij为

(3)

计数区域内磨粒的平均间距定义为

(4)

按式(3)、(4)算得两种砂带的平均间距，如表1所示.

2.3 磨粒排布方式

(5)

为防止磨粒之间产生干涉，在位移叠加过程中应满足任意i、j两磨粒之间距离大于其半径之和，即

(6)

式中，dgi为第i颗磨粒的直径，dgj为第j颗磨粒的直径.

若不满足式(6)所述的磨粒距离与半径和关系，则说明在数值形貌的生成过程中存在磨粒干涉现象.此时将干涉磨粒重新赋予随机位移，再次验证，直到所有磨粒不存在干涉位置.砂带虚拟形貌的生成流程如图5所示.

图5 砂带虚拟形貌生成流程图Fig.5 Flow chart of abrasive belt’s virtual surface generation

2.4 位移叠加次数

磨粒在基材平面整齐分布的模型如图6(a)所示，不同直径的磨粒依据磨粒间距均匀分布在砂带表面，在此基础上，对所有磨粒施加单次随机位移.若干次随机位移叠加后，得到图6(b)所示的磨粒随机分布模型.

随机位移的叠加次数越多，磨粒分布随机性越好，更接近实际砂带特征.然而，无限制地增加位移叠加次数将影响模型建立效率，增大模型计算量.而较少的位移叠加次数会影响虚拟砂带形貌的磨粒排布与真实性.为达到理想的虚拟形貌建模效率，需对磨粒的位移叠加次数进行讨论.

在砂带表面建立如图6(b)所示的若干竖直面如A、B、C、D……，统计在位移叠加次数为mi(i=1，2，3,…)时，与竖直面相干涉的磨粒数目Nai、Nbi、Nci、Ndi……等数据，并计算在相同位移叠加次数下不同竖直相干涉的磨粒数目方差.所获方差越小意味着砂带磨粒随机性越好.

图6 磨粒排布随机性评价Fig.6 Evaluation of grains distribution randomicity

现以36与24两种粒度建立800颗以磨粒平均间距排列的20×40磨粒阵列，选取10个竖直面在位移叠加次数为100至1000时统计与该竖直面相干涉的磨粒数目方差，汇总于图7.

图7 位移叠加次数与干涉磨粒方差的关系

Fig.7 Relationship between superposition frequency and va-riance of interfere grains number

随位移叠加次数的增加，与竖直面相干涉的磨粒数目方差逐渐变小，这意味着磨粒的分布趋于均匀.同时注意到叠加次数为600左右时，方差变化率出现差异：当位移叠加次数小于600时，方差减小明显，但次数达600以后方差减小趋势明显放缓且出现波动.这说明随机位移叠加次数达到600时磨粒已达到较好的均匀性，继续增加叠加次数只会增加意义不大的计算量.

3 数值形貌与测量结果

为验证单颗磨粒多面体的模型及磨粒叠加随机位移排布的正确性，设计对应参数的测量来评价实际砂带表面，统计分析磨粒出刃高度、磨粒间距来进行研究，分别以粒度号为36及24的砂带为例，比较砂带模拟形貌与实际形貌的相似程度.

3.1 砂带出刃高度与磨粒间距

单颗磨粒模型与实际磨粒形状是否接近主要体现于砂带的出刃高度上.图8(a)、8(b)所示为36粒度与24粒度两种砂带在未钝化条件下出刃高度的测量值与仿真模型值的对比.两砂带出刃高度测量值的概率柱状图走势与正态分布极为类似，但分布规律存在偏峰特征，这可能与磨粒埋入胶层深度的随机性有关.磨粒的仿真值与测量值之间有着极为接近的均值与分布规律，但存在些许偏差，主要表现为砂带表面的测量值更集中分布于均值附近，这意味着实际砂带表面一致性较好.通过两者出刃高度的统计分析，磨粒的多面体建模方式可以在多颗磨粒构成的砂带表面获得相似的出刃高度均值与分布规律，可以证明单颗磨粒三维模型的合理性.

图8 砂带出刃高度分布Fig.8 Distribution of grains protrusion height

采用随机位移叠加的方式进行磨粒随机排布主要改变了磨粒之间的距离.图9(a)、9(b)分别为粒度为36、24两种砂带磨粒间距的仿真模型与实际测量值的对比.测量值与模型值均呈现由均值部分向两侧逐渐递减的特征.磨粒经过多次随机位移的叠加之后可以获得与实际形貌相似的间距，可以证明磨粒叠加随机位移的方式来模拟砂带磨粒均匀分布的有效性.

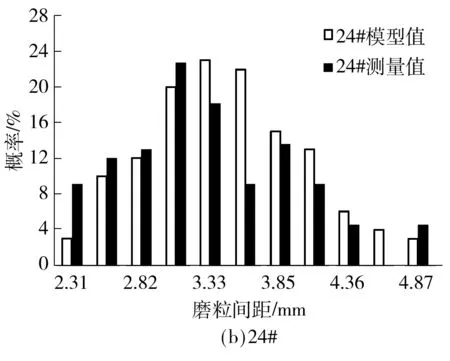
图9 砂带磨粒间距分布Fig.9 Distribution of grains spacing

3.2 钝化砂带出刃高度预测

磨粒通常为硬脆材料，其破坏方式以折断破碎为主.Chen等[15]认为，由于磨粒的机械属性与几何属性的随机性，导致磨粒折断高度带有随机特征，并给出了磨粒折断高度h的预测模型：

h=δ+h′[sin(ωx+φ)+1]

(7)

式中：δ为磨粒切深，与砂带磨削工艺参数及服役时间有关[19]；h′为折断幅值；ω为随机折断频率；φ为随机折断相位角.图10所示为磨粒受到随机折断影响后的形状变化.

Hou等[14]指出，磨粒中磨具磨粒仅有出刃高度位于前18.7%的磨粒参与磨削.假设该部分磨粒发生破碎，改变磨粒形状，则可根据上述两条件构建砂带钝化后出刃高度的统计规律.

图10 磨粒折断轮廓形状Fig.10 Grain fracture contour generated by worn

使用图11所示的砂带磨削实验机开展相关实验研究.实验机采用交流电动机驱动砂带高速转动，气缸将工件贴紧砂带进行磨削.力与速度由控制箱直接控制，同时可通过传感器进行反馈校正.工件材料为U71 Mn，对其在200 N正压力下，以30 m/s的磨削速度磨削60 s.

图11 砂带磨削实验机Fig.11 Abrasive belt grinding apparatus

图12(a)、12(b)分别为36与24粒度折断磨粒的砂带虚拟形貌与钝化砂带表面磨粒出刃高度统计图.相比于新砂带，磨粒出刃高度变化较大，但仍然呈现由均值向两侧递减的特征.砂带的出刃高度均值减小，但分布更加集中于均值附近，这说明钝化砂带表面高度一致性较好.此外，折断磨粒的砂带虚拟形貌与钝化表面磨粒出刃高度规律极为类似.但在出刃高度均值附近时，所建立的虚拟形貌与真实值出现差异，这是由于实际砂带中出刃高度较高的磨粒以折断方式钝化，而其他磨粒特别是出刃高度较低磨粒不止存在单一折断情况.

综上所述，以上虚拟形貌各参数与实际砂带形貌对应参数的比较表明，砂带虚拟形貌能够较好地描述实际砂带形貌特征.此外，在钝化砂带形貌预测中，虚拟形貌能够展示出经折断后钝化砂带出刃高度的分布情况，与实际砂带钝化形貌较为相似.实验结果也验证了包括磨粒三维模型、表面磨粒辨识和磨粒随机排布的砂带虚拟形貌建模方法的合理性.

图12 钝化砂带出刃高度分布Fig.12 Distribution of blunt abrasive belt protrusion height

4 结论

(1)提出一种采用随机平面切割立方体以建立磨粒模型的方法，获得了具有特定长宽比的磨粒多面体模型.以刀尖角作为判别标准，在构造磨粒模型的切面数目达到24-30左右时，磨粒模型能够较好地描述实际磨粒特征.

(2)砂带磨粒在基材上的随机分布规则可通过多次赋予磨粒在基材表面随机位移的方式进行模拟.当位移叠加次数达到600左右时，磨粒在基材上已基本达到均匀分布.

(3)实际砂带的出刃高度及磨粒间距均呈现由均值向两侧递减的现象，并且带有明显的偏峰特征.钝化砂带的磨粒出刃高度均值降低，一致性变好.此外，部分采用折断磨粒建立的砂带虚拟形貌能够描述钝化砂带特征.

参考文献：

[1] DATE S W,MALKIN S.Effects of grit size on abrasion with coated abrasives [J].Wear,1976,40(2):223- 235.

[2] MERCER A P,HUTCHINGS I M.The deterioration of bonded abrasive papers during the wear of metals [J].Wear,1989,132(1):77- 97.

[3] 宿崇.虚拟磨削关键理论及其技术的研究 [D].沈阳：东北大学,2009.

[4] DOMAN D A,WARKENTIN A,BAUER R.A survey of recent grinding wheel topography models [J].International Journal of Machine Tools & Manufacture,2006,46(3):343- 352.

[5] PELLEGRIN De V D,STACHOWIAK G W.Evaluating the role of particle distribution and shape in two-body abrasion by statistical simulation [J].Tribology International,2004,37:255- 270.

[6] HISAKADO T,SUDA H.Effects of asperity shape and summit height distributions on friction and wear characteristics [J].Wear,1999,225(98):450- 457.

[7] 刘月明,巩亚东,曹振轩.基于数值建模的砂轮形貌仿真与测量 [J].机械工程学报,2012,48(23):184- 190.

LIU Yue-ming,GONG Ya-dong,CAO Zhen-xuan.Analysis of numerical grinding wheel topography and experiment measurement [J].Journal of Mechanical Engineering,2012,48(23):184- 190.

[8] 张祥雷，姚斌，冯伟，等.基于多颗磨粒随机分布的虚拟砂轮建模及磨削力预测 [J].航空学报，2014,35(12):3489- 3498.

ZHANG Xiang-lei,YAO Bin,FENG Wei,et al.Modeling of virtual grinding wheel based on random distribution of multi abrasive grains and prediction of grinding force [J].Acta Aeronautica Sinica，2014,35(12):3489- 3498.

[9] 曹有为,乔国朝.砂轮表面形貌仿真方法研究 [J].金刚石与磨料磨具工程,2016,36(3):33- 37.

CAO You-wei,QIAO Guo-zhao.Simulation method of grinding wheel topography [J].Diamond & Abrasive Engineering,2016,36(3):33- 37.

[10] 吕长飞,李郝林.外圆磨削砂轮形貌仿真与工件表面粗糙度预测 [J].中国机械工程,2012,23(6):40- 45.

LÜ Chang-fei,LI Hao-lin.Simulation of wheel topography and forecasting of roughness in cylindrical grinding [J].China Mechanical Engineering,2012,23(6):40- 45.

[11] 王志伟,俞冬强,陈佳杰,等.磨粒的几何形状研究综述 [J].现代制造工程,2008(11):1- 4.

WANG Zhi-wei,YU Dong-qiang，CHEN Jia-jie,et al.Review on the shape of abrasive particle [J] Modern Manufacturing Engineering,2008(11):1- 4.

[12] WANG W,LI J,FAN W,et al.Characteristic quantitative evaluation and stochastic modeling of surface topo-graphy for zirconia alumina abrasive belt [J].International Journal of Advanced Manufacturing Technology,2017,89(9/10/11/12):3059- 3069.

[13] YAO P,GONG Y,MATSUDA T,et al.Investigation of wheel wear mechanisms during grinding optical glasses through statistical analysis of wheel topography [J].International Journal of Abrasive Technology,2012,5(1):33- 47.

[14] HOU Z B,KOMANDURI R.On the mechanics of the grinding process(Part I):Stochastic nature of the grinding process [J].International Journal of Machine Tools & Manufacture,2003,43(15):1579- 1593.

[15] CHEN X,ROWE W B.Analysis and simulation of the grinding process(Part I):Generation of the grinding wheel surface [J].International Journal of Machine Tools & Manufacture,1996,36(8):871- 882.

[17] BLUNT L,EBDON S.The application of three-dimensional surface measurement techniques to characterizing grinding wheel topography [J].International Journal of Machine Tools & Manufacture,1996,36(11):1207- 1226.

[18] DARAFON A,WARKENTIN A,BAUER R.Characterization of grinding wheel topography using a white chromatic sensor [J].International Journal of Machine Tools & Manufacture,2013,70(7):22- 31.

[19] 任敬心,华定安.磨削原理 [M].北京：电子工业出版社,2011.