无线携能协作传感器网络的能效研究*
2017-04-24阔永红周碧荣陈健
阔永红 周碧荣 陈健
(西安电子科技大学 通信工程学院, 陕西 西安 710071)
协作传感器网络(CWSN)通过各节点的相互协作来提高整个网络的能效,是一种提高能量利用率的有效通信手段.广泛应用于医疗、环境、军事等方面[1- 2].协作传感器网络通常由低功耗传感器节点构成,这些节点利用储能有限的电池进行通信[3],很大程度制约了传感器网络的寿命.携能通信协作传感器网络是在传统的CWSN中采用无线携能通信技术(SWIPT),使得同一射频信号不仅可以用于信息传输,还能通过能量收集技术(EH)获取能量,为CWSN提供持久稳定的能量来源[4- 5].
文献[6- 8]中对采用携能通信技术CWSN进行了研究,分析网络的中断性能与能效.文献[6]中针对CWSN中引入SWIPT后的能效问题,提出了资源分配策略使能效最大.文献[7]在动态能量水平携能通信CWSN中,采用马氏链方法构建节点的动态能量模型,并对中断概率进行分析,文献[8]中为了获得更好的数据速率以及较低的中断概率,制定了最大最小化中继选择策略.文献[9- 11]在动态能量下的绿色传感器网络中,通过合理分配资源使传输速率达到最大化.但其均采用太阳能来收集能量,相比于太阳能,基于射频(RF)的SWIPT可以实现能量和信息并存,而且不受环境制约.此外,上述文献中的CWSN均采用基于信道状态下的协作方式,该协作方式会导致靠近信源的中继节点承担较多的业务,能量消耗过快,不公平的协作方式导致网络过早死亡,同时对于节点电池容量有限且时时变化情况下如何高效地使用每一时隙的电池能量未做深一步的研究.
综上所述,针对携能协作传感器网络中电池容量有限以及能量效率低的问题,笔者分析了节点电池能量在长时间内的动态变化,并最大化了平均能效,使传感器网络的节点电池能量更有效利用.其中,对于协作通信中存在节点负载不均造成网络过早死亡的问题,提出了动态能量协作策略,通过均衡节点之间的负载,延长了网络的寿命.最后通过仿真实验验证了所提出的动态能量协作策略下的平均能效达到最优,同时系统的吞吐量保持在较高的水平.
1 系统及通信模型
1.1 系统模型
传感器节点随机分布在S和N区域中且均具有RF能量收集的能力,假设S区域当前处于信息密集区,即有大量的信息需要被发送,而N区具有自己的信息,但是信息较S区域少,主要作用是协助S区节点,系统模型如图1所示.
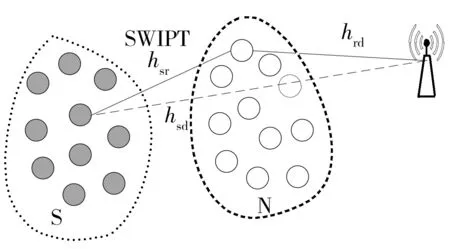
图1 系统模型Fig.1 System model
在该模型之下每个传感器节点都可以工作在信息传输和能量传输的状态[10].当S域中节点有大量的信息需要传输时,它可以选择直传模式或中继模式,N区域节点电池容量如表1所示.表中,Eh(j)表示在j时隙中节点收集的能量,Er(j)表示在j时隙内中继消耗的能量.
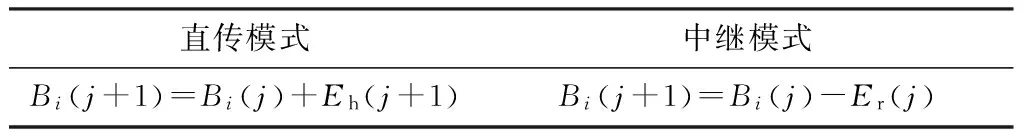
表1 节点电池状态之间的转换Table 1 Conversion between the nodes in the battery status
由于现有研究中硬件电路的限制,信号处理单元与能量收集单元无法同时运行[10],因此在文中采用功率分割(PS)的方式,功率分割系数为ρ.为了能够提高能效,承担中继的传感器节点协作协议为解码传输(DF).
1.2 通信模型
在上述网络中,考虑了两种信息传输模式:直传模式和中继模式,为了避免中继选择时节点由于反馈状态信息造成不必要的浪费以及均衡节点之间的负载,提出了动态能量协作策略,该策略取决于信道状态及N区域节点能量水平,当N区域的某节点能量水平达到一定的阈值且满足
max{ri}>rsd
(1)
时,则该节点承担中继.式(1)中rsd表示源端到中继端的信道状态,ri代表经过中继的源节点到基站的信噪比(SNR).对于DF中继而言,
ri=min(r1,i,r2,i)
(2)
式中,r1,i代表着第一跳中源端到中继的SNR,r2,i代表着第二跳中继到目的端的SNR.
假设信道在一个时隙内保持不变,且不同时隙间信道状态独立,信道状态服从瑞利分布[12],hSRi、hRiD、hSD分别表示源端至中继端Ni、中继端Ni到基站以及源端到基站的信道系数,hSRi、hRiD、hSD服从均值为0,方差为δSRi=E[|hSD|]2、δRiD=E[|hRiD|]2以及δSD=E[|hSD|]2的高斯分布.将信道状态归一化,得到gsr|hSRi|2/δSRi、grd|hRiD|2/δRiD和gsd|hSD|2/δSD.其中为传输端i到接收端j之间的距离,α为路径衰减指数,Kij表示归一化的常数,由环境决定.
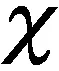
端到端的吞吐量为
(3)
式中,B表示信道带宽.
设通信链路下的总发送功率为Psd,当节点收集到的能量足够传输信息时,Psd为
Psd=Ps
(4)
Pr=Ph=η(1-ρ)Ps|hsr|2
(5)
式中,η为能量收集过程中的转化效率,Ph为传感器节点接收到的信息能量.
当节点收集到能量不足以传输信息时,Psd为
Psd=Ps+Pr
(6)
式中,
Pr=Ph+Po
(7)
从式(3)中得知:当gsdPs+grdPr=ρgsrPs时,链路速率达到最大化.联合式(5)、(6)可求解出
(8)
在直传模式下,Ps=Psd,Pr=0.联合式(8)可得到等效信道增益Gsd为
(9)
在上述分析基础上,端到端的吞吐量为
(10)
式中,当v=1时网络传输为直传模式,v=0时网络传输处于中继模式.
2 性能分析
作为能量受限的传感器网络,使用能量收集延长传感器的寿命非常有效,同时将所收集的能量合理利用,提高能量的利用率也是必要的.因此文中将能效作为性能的衡量标准.
2.1 系统能效
整个网络的系统吞吐量为
(11)
式中,K和N分别表示源节点和中继节点的数目,αs,r表示中继指示系数,t为时间.
整个网络消耗的功率为
(12)
式中,Pcs、Pcr分别表示源节点和中继节点的固有电池损耗.
将网络的平均能效定义为
Ueff(Ps(t),ρ(t),v(t))=
(13)
2.2 性能优化
(14)
由于限定条件式(14-1)涉及到马氏链(MDP)中状态转移的问题,MDP计算相对比较集中会导致计算能力有限的传感器节点难以承担,因此需要对限定条件(14-1)进行一些处理,在首次进行功率分配时,令B1=E0为初始能量.由于电池容量的有限性,当在B(t-1)+Eh(t)-Er(t-1)>M条件下时,收集的能量将会被丢弃,为了保证无能量被丢弃,限定条件应为B(t-1)+Eh(t)-Er(t-1)≤M.
限定条件(14-1)可以被解析为
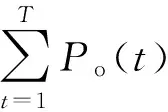
(15)
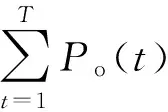
(16)
通过上述转化,优化函数变为
(17)
该函数限定条件为式(14-2)-(14-7)、式(15)和式(16).
2.3 目标函数的转换
优化函数(17)是非凸函数,为了便于求解,将优化函数(17)通过非线性规划,由分式规划转化为减式规划[13],定义最大的加权能效q*为
(18)
引理1 在U(Psd(t),ρ(t),v(t))>0且UTP(Psd(t),ρ(t),v(t))>0条件下,当式(19)满足时,式(18)中的q*是存在的:
Tq*UTP(Psd(t),ρ(t),v(t)))=
(19)
引理1的证明与文献[14]中的附录A类似.引理1表明优化问题(17)中的目标函数可以由一个减式表达式替代,且两者具有同样的优化解.
根据引理1可将优化问题(17)的目标函数转化为
TqUTP(Psd(t),ρ(t),v(t))
(20)
为了便于求解,假设在T为首次处于中继模式的时间,即T-1时间中v=1,在最后一个时隙v=0;同时假设端到端的信噪比远远大于1,且因为0≤ρ≤1,因此将Gsd与Po近似为
(21)
(22)
定理1 经过转化的目标函数(20)及优化问题(17)中的限定条件是关于Psd、ρ的凸优化函数.
证明令目标函数为f(Psd,ρ,v)=U(Psd(t),ρ(t),v(t)-TqUTP(Psd(t),ρ(t),v(t))),对f求汉森矩阵,即
(23)
2.4 叠加算法
文中采用叠加算法(丁克尔巴赫方法)[13]解决问题(19),算法步骤可表述如下:
步骤1 令j=1,q=0;
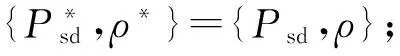
步骤3 求解优化问题(17),获得最优解{Psd,ρ};
步骤4 如果U(Psd,ρ)-TqUTP(Psd,ρ)<ξ,则进入步骤5,否则进入步骤7;
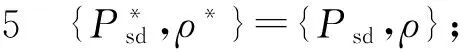
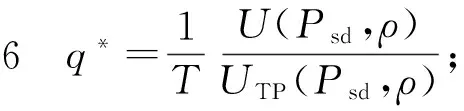
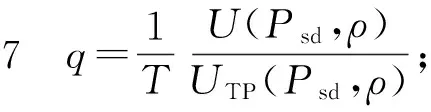
步骤8j=j+1,返回步骤2.
2.4.1 对偶问题
为了求解出优化函数式(19)的资源分配问题,采用丁克尔巴赫叠加算法和拉格朗日对偶分解相结合的方法来求解.
表达式(23)表述了关于优化问题(19)的拉格朗日函数:
L(ω,v,μ,φ,ψ,ε,σ,Psd,ρ)=
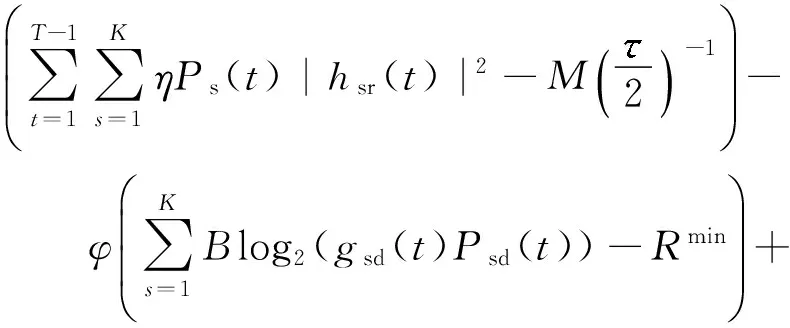
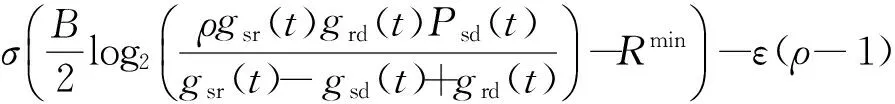
(24)
式中,T1表示中继转发占用的时隙,ω和ϑ为关于中继从电池中消耗能量限制的拉格朗日乘子,μ为关于发送功率限制的拉格朗日乘子,ψ为关于系统吞吐量的限定的拉格朗日乘子,ε为关于功率分割系数的拉格朗日乘子.
该对偶问题可表述为
(25)
使用丁克尔巴赫法求解式(25),在每一次的迭代过程中,给定对偶变量,采用库恩塔克条件求出主变量为
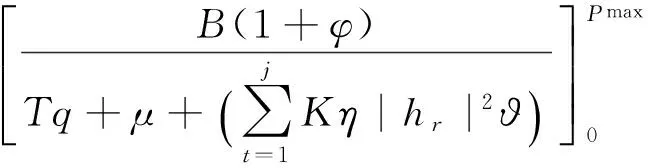
(26)
(27)
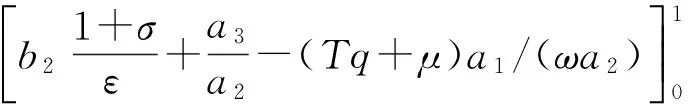
(28)
其中,a1=gsr-gsd+grd,a2=gsr+ηgrd|hsr|2,a3=gsd+ηgrd|hsr|2,b2=B/(2ln2).在给定主变量的情况下,利用梯度下降法,通过式(29)-(34)更新对偶变量:
ω(j+1)=[ω(j)-
(29)
ϑ(j+1)=[ϑ(j)-
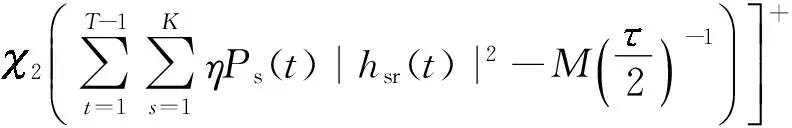
(30)
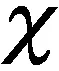
(31)
ψ(j+1)=[ψ(j)+
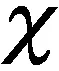
(32)
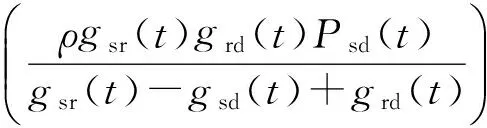
(33)
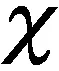
(34)
3 仿真结果分析
假设S区中心与N区中心的距离为120 m,与基站的距离为650 m.S区有100个节点,每个节点带宽B=3 MHz,中继N=5;路径衰减指数α=2,归一化Kij=1,能量转换效率η=0.8;加性高斯白噪声的方差分别为δsr=-120 dBm、δsd=-130 dBm、δrd=-110 dBm.最小吞吐量要求Rmin=2 Mb/s,叠加算法中最大的叠加次数Itermax=20,收敛参数ξ=0.001[6],源端和中继端固有的电池损耗Pcs+Pcr=0.05[7].
针对文中所提出的丁克尔巴赫法与拉格朗日对偶法相结合的算法,假设电池容量为0.5 J,图2阐明了不同发送功率及最大叠加次数之下的能效变化趋势。由图2可看出,能效随着叠加次数增加而增加,最终收敛于第10次叠加,证明了本文算法的有效性.从图2中可以看出较高的最大发送功率可以带来更好的能效,表现出此种趋势是由于较高最大传输功率可以带来更大发送功率和数据速率的效益,从而使能效最大化.
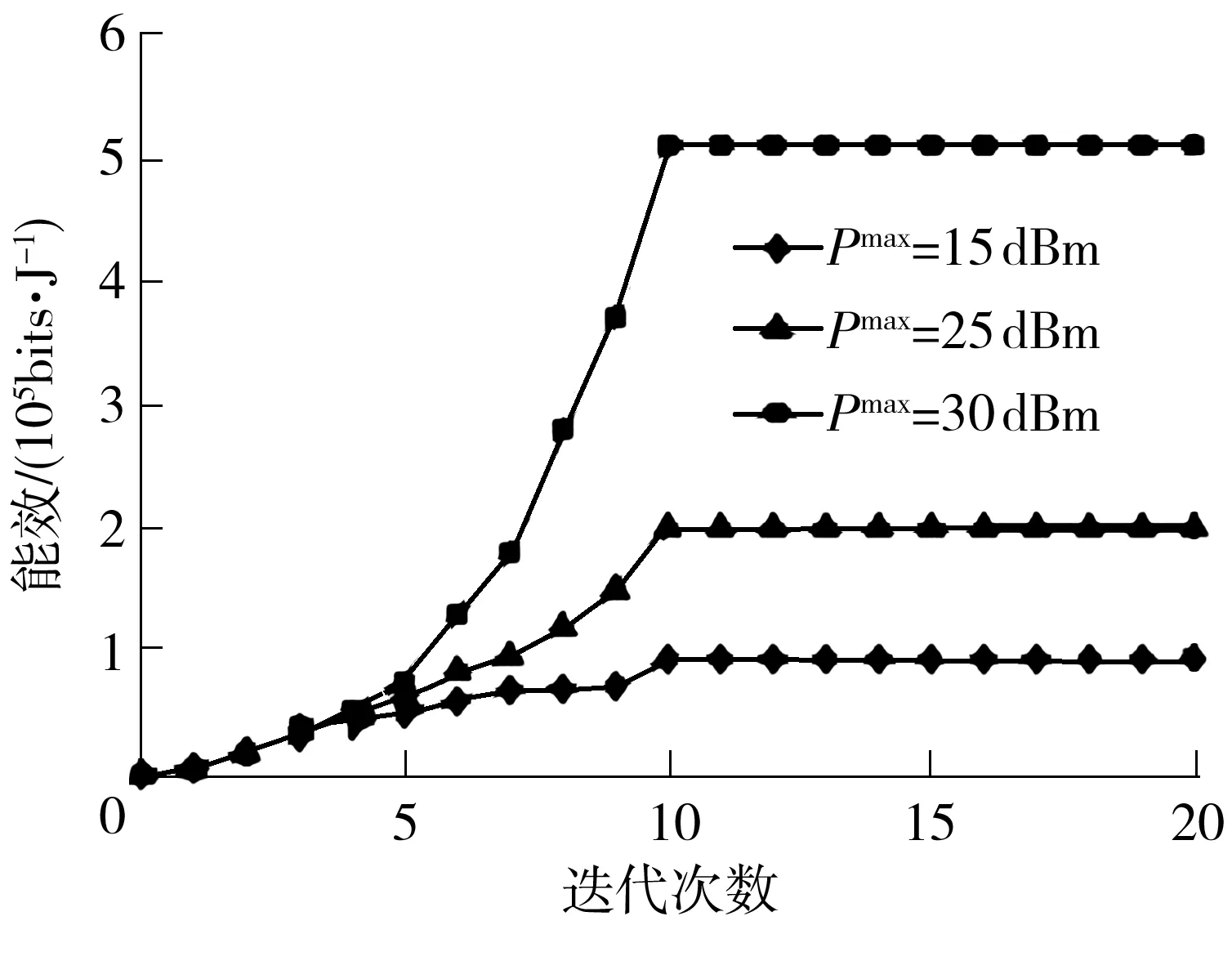
图2 能效与迭代次数的关系Fig.2 Energy efficiency versus the number of iterations
在图3中,随着最大传输功率的变化,在不同电池容量之下能效曲线呈现不同的变化趋势.随着最大发送功率增大,能效也呈现上升趋势,当最大发送功率达到30 dBm时,能效收敛.这是因为在这个时刻吞吐量与总消耗功率的比值达到最大,虽然此时吞吐量不一定是最大的,但是所消耗的单位能量下的吞吐量是最大的.同时,在不同的电池容量之下,网络所达到的能效不一样,由于每个时隙中电池能量水平的不同,导致总发送功率受到限制,如果当前时隙电池所储电量不能达到最大发送功率所需求的值,则该通信链路中发送功率的最大发送功率限制将变为当前电池能量.因此,随着电池容量的增加,所存储的电量将会更多,通信过程中,发送功率不会受到电池的限制,在电池容量不断增加的情况下,网络能效也呈现增长的趋势.当电池容量低时,影响发送功率的主要因素是当前电池能量水平,当电池容量高时,发送功率则只受到最大发送功率的限制.因此从图3中可得,当电池容量增长到一定水平时,将不会成为影响系统性能的因素.
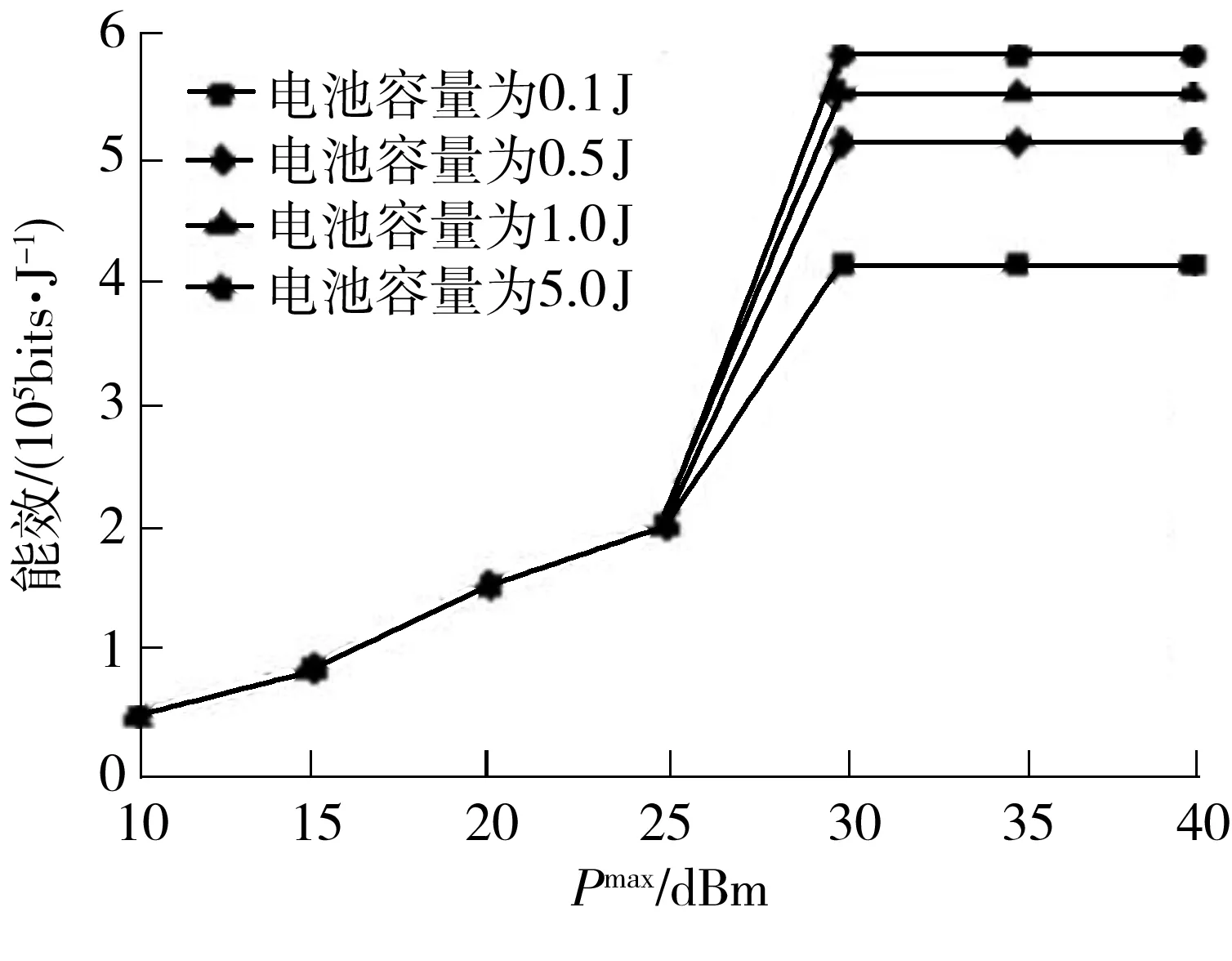
图3 能效随不同电池容量的变化Fig.3 Energy efficiency for different energy storage
图4与5电池容量均为0.5 J.图4示出了文中提出的基于能效的资源分配策略与文献[15]中基于吞吐量的资源分配策略在能效方面的对比.由图4可知,以追求吞吐量最大化为目标时,能效会在功率逐渐增大时越来越小,最终由于电池容量的限制趋于平稳.图5示出了优化目标不同的两种资源分配策略在吞吐量方面的性能对比,文中提出的基于能效的资源分配策略相比于文献[15]所提出的策略,在吞吐量方面虽有下降,但是依旧保持在较高的吞吐量水平.综合图4和5可以得出:在发送功率较低的情况下,笔者所提出的策略并不占很大的优势,但是在发送功率逐渐升高的情况下,笔者所提出的策略在均衡吞吐量和能效方面具有很大的价值.

图4 不同策略下的能效比较Fig.4 Comparison of energy efficiency for different targets
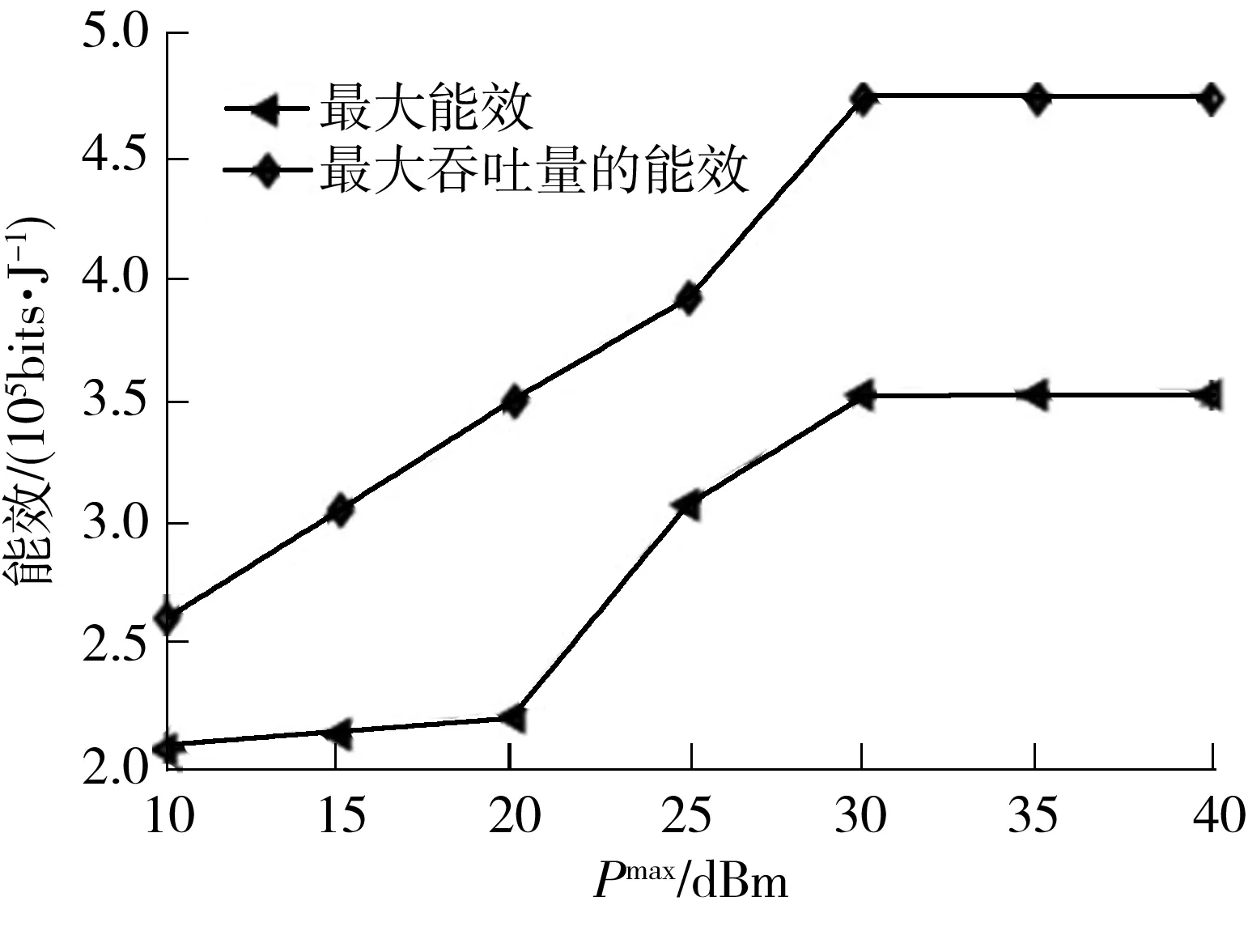
图5 不同目标下的吞吐量比较Fig.5 Comparison of throughput for different targets
4 结语
文中在携能协作传感器网络中,综合考虑实际通信节点电池容量有限和电池能量水平动态变化的特性,对网络进行建模分析与性能优化,针对传感器网络能量利用率低的问题,通过凸优化方法实现网络能效的最大化,并针对传感器网络节点能量收集过程与数据传输过程相互制约的特性,提出一种动态能量协作策略来延长网络寿命.仿真分析结果表明,在保证一定吞吐量和传输限制的前提下,文中所提出的能量分配方案和动态协作策略相比于传统研究方案,可以使携能协作传感器网络具有更高的系统能效.
参考文献:
[1] RAUIT T,BOUABDALLAH A,CHALLAL Y.Energy efficiency in wireless sensor networks:atop-down survey [J].Computer Networks,2014,67:104- 122.
[2] LI Bin,LI Hong-xiang,WANG Wen-jie,et al.Performance analysis and optimization for energy-efficient cooperative transaction in random wireless sensor network [J].IEEE Transactions on Wireless Communications,2013,12(9):4647- 4657.
[3] 胡小青,胥布工,文莎,等.一种能量平衡的最优分布式成簇机制 [J].华南理工大学学报(自然科学版),2012,40(8):1- 7.
HU Xiao-qing,XU Bu-gong,WEN Sha,et al.An energy-balanced optimal distributed clustering mechanism [J].Journal of South China University of Technology(Natural Science Edition),2012,40(8):1- 7.
[4] CHEN He,LI Yong-hui,JIANG Yun-xiang,et al.Distributed power splitting for SWIPT in relay interference channels using game theory [J].IEEE Transactions on Wireless Communications,2015,14(1):410- 420.
[5] DING Zhi-guo,KRIKIDIS I,SHARIF B,et al.Wireless information and power transfer in cooperative networks with spatially random relays [J].IEEE Transactions on Wireless Communications,2014,13(8):4440- 4453.
[6] GUO S,WANG F,YANG Y,et al.Energy-efficient co-operative transmission for simultaneous wireless information and power transfer in clustered wireless sensor networks [J].IEEE Transactions on Communications,2015,63(11):4405- 4417.
[7] LIU K H.Performance analysis of relay selection for co-operative relays based on wireless power transfer with finite energy storage [J].IEEE Transactions on Vehicular Technology,2016,65(7):5110- 5121.
[8] MAHAMA S,ASIEDU D K P.Relay selection based on simultaneous wireless information and power transfer for wireless sensor networks [J].International Journal of Computer Engineering and Information Technology,2017,9(1):1- 5.
[9] AMIRNAVAEI F,DONG M.Online power control optimization for wireless transmission with energy harvesting and storage [J].IEEE Transactions on Wireless Communications,2016,15(7):4888- 4901.
[10] MAO Z,KOKSAL C E,SHROFF N B.Nearoptimal po-wer and rate control of multi-hop sensor networks with energy replenishment:basic limitationswith finite energy and data storage [J].IEEE Transactions on Automatic Control,2012,57(4):815- 829.
[11] SRIVASTAVA R,KOKSAL C E.Basic performance li-mits and tradeoffs in energy-harvesting sensor nodes withfinite data and energy storage [J].IEEE/ACM Transactions on Networking,2013,21(4):1049- 1062.
[12] LEE S,ZHANG R,HUANG K.Opportunistic wireless energy harvesting in cognitive radio networks [J].IEEE Transactions on Wireless Communications,2013,12(19):4788- 4799.
[13] DINKELBACH W.On nonlinear fractional programming [J].Management Science,1967,13(7):492- 498.
[14] NG D W K,LO E S,SCHOBER R.Wireless information and power transfer:energy efficiency optimization in OFDMA systems [J].IEEE Transactions on Wireless Communications,2013,12(12):6352- 6370.
[15] LEE H,LEE K J,KIM H,et al.Resource allocation techniques for wireless powered communication networks with energy storage constraint [J].IEEE Transactions on Wireless Communications,2016,15(4):2619- 2628.
