三倍体毛白杨生长量数学模型建立及验证
2017-04-22佘生斌李小华黄志刚李海俊
佘生斌 ,李小华, 黄志刚 ,李海俊
(汉中市林业科学研究所,陕西 汉中 723000)
三倍体毛白杨生长量数学模型建立及验证
佘生斌 ,李小华, 黄志刚 ,李海俊
(汉中市林业科学研究所,陕西 汉中 723000)
为了探索三倍体毛白杨生长节律和预测生长趋势,通过对汉中市林研所院内18年生三倍体毛白杨标准木各生长量的解析,并运用线性和非线性回归分析对比,初步建立了幼林期材积、胸径、树高生长量的最佳数学模型。结果表明,最佳材积总生长量数学模型为:v=0009a2.318,最佳胸径总生长量数学模型为:D=-0.0186a2+1.9145a+0.1943,最佳树高总生长量数学模型为:H=2.9392a0.7459。研究结果为预测三倍体毛白杨的生长趋势提供科学依据。
三倍体毛白杨;生长模型
杨树(PopulusL.)是世界范围广泛分布的阔叶用材树种,生长快,适应性强,成才早,更新快,是我国的主要造林树种之一[1]。三倍体毛白杨(TriploidP.tomentosa)是北京林业大学组织多方力量协作攻关,从大花粉观察、天然三倍体选种和人工育种三方面着手,采取回交部分染色体替换和配子染色体加倍综合技术,经过15年的研究,人工诱导培育的第一个多倍体乔木新品种[2],生长快,材质好,抗病虫,是我国当前短周期工业用材林首选树种[3]。
林木生长量模型在研究林木生长变化规律及预测林木生长量方面具有重要作用,一直受到国内外林业工作者的高度重视[4]。已经有大量的关于不同树种基于全林分或单木的生长量、生物学模型被提出,且部分已经用于林业生产实践[5],但关于三倍体毛白杨生长量模型的研究却鲜见报道,只有刘淑春等(2005)研究了引种到湘南的三年生的三倍体毛白杨的生长模型[6]。树木生长发育规律受树种特性及生长环境条件的影响,不同树种、同一树种在不同生长发育阶段,以及在不同地区及不同立地的生长规律都不尽相同。本研究以18年生三倍体毛白杨为对象,运用线性[7]和非线性回归分析[8]方法进行数据拟合,选择最佳拟合公式,建立了用于三倍体毛白杨生长量预测的数学模型,为该树种的集约化经营提供科学依据。
1 材料与方法
1.1 材料
材料选汉中市林研所栽植的18年生三倍体毛白杨,生长地海拔560 m,属北亚热带季风气候,年均温14.5 ℃,日照时数1 300~1 800 h,年均降雨量1 100 mm,黄棕壤土质,土质粘重,pH值6.5,肥力中等。
1.2 方法
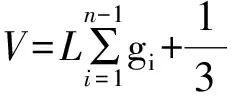
2 结果与分析
2.1 材积总生长量模型
材积的生长同时受胸径和树高生长的影响,对解析木前7组材积总生长量数据分别进行线性拟合(图1)、幂指数拟合(图2)、二次曲线拟合(图3)及对数拟合(图4),发现三倍体毛白杨材积生长趋势拟合最好的是二次曲线,拟合优度R2=0.997,其次是幂指数拟合,R2=0.996 8,说明材积总生长量趋势符合曲线模式。由4种曲线图可以看出,材积总生长量在前4年慢速增长,从第4年到第18年快速增长,到第18年出现拐点,生长减慢。用第8、第9组数据所代表的年龄(a),分别用4种拟合公式计算材积(V)预测值,然后用实际测量值进行相对误差检验(详见表1),发现幂指数拟合公式预测精度更高,相对误差均小于0.04,综合拟合优度最大和数据验证的相对误差最小,确定材积总生长量数学模型最佳应为:V=0.000 9a2.318R2=0.996 8,上式中V表示材积总生长量,a表示树木年龄。
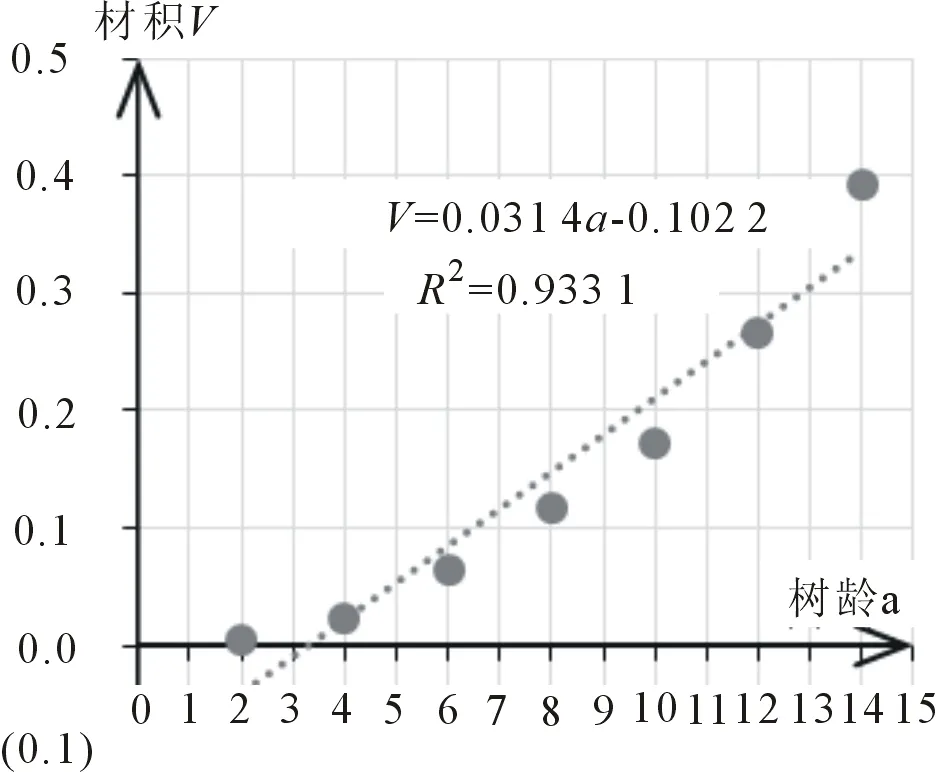
图1 材积线性拟合
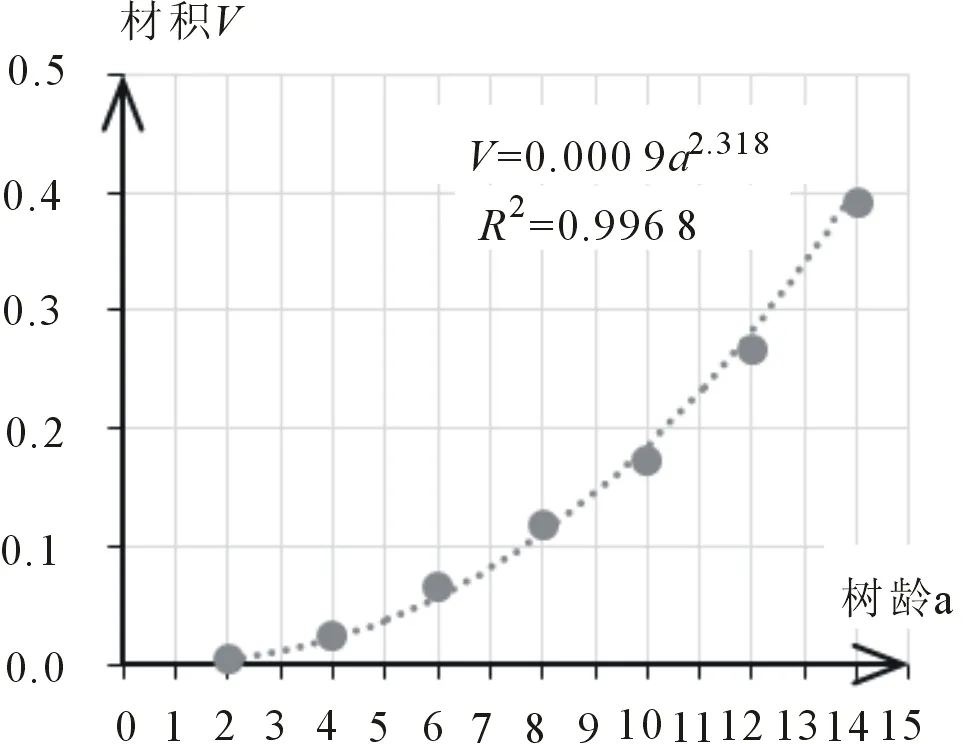
图2 材积幂指数拟合
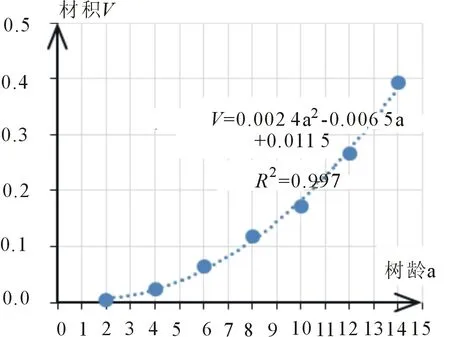
图3 材积二次曲线拟合

图4 材积对数拟合

编号实际值线性公式预测值相对误差幂指数公式预测值相对误差二次曲线公式预测值相对误差对数公式预测值相对误差80.56860.40020.29610.55640.02140.52190.08210.30150.469790.70640.46300.34460.73110.03490.67210.04860.32250.5435
2.2 胸径总生长量模型
对解析木前7组胸径总生长量数据分别进行线性拟合(图5)、幂指数拟合(图6)、二次曲线拟合(图7)及对数拟合(图8),由拟合的曲线图可以看出,胸径总生长量近似线性增长模式,从第2年到第18年呈直线增长,说明三倍体毛白杨缓苗快,第2年开始就进入快速生长期,前18年生长旺盛,未达到数量成熟龄。线性、幂指数、二次曲线都拟合较好,拟合优度分别为0.997 1、0.996 3、0.998 7。用第8、第9组数据所代表的年龄(a),分别用4中拟合公式计算胸径(D)预测值,然后用实际测量值进行相对误差检验(详见表2),拟合最好的是二次曲线,相对误差均小于0.02,综合拟合优度最大和数据验证的相对误差最小,胸径总生长量数学模型最佳应为:
D=-0.018 6a2+1.914 5a+0.194 3
R2=0.9987
上式中D表示胸径总生长量,a表示树木年龄。
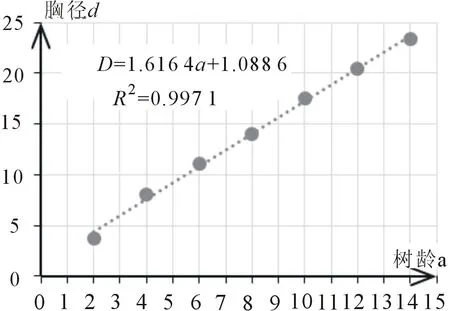
图5 胸径线性拟合

图6 胸径幂指数拟合

图7 胸径二次曲线拟合

图8 胸径对数拟合

编号实际值线性公式预测值相对误差幂指数公式预测值相对误差二次曲线公式预测值相对误差对数公式预测值相对误差826.5726.950.0127.050.0226.060.0222.590.15928.6630.180.0530.190.0528.630.0023.760.17
2.3 树高总生长量模型
对解析木前7组树高总生长量数据分别进行线性拟合(图9)、幂指数拟合(图10)、二次曲线拟合(图11)及对数拟合(图12),由4种曲线图可以看出,树高总生长量也近似线性增长模式,从第2年开始就进入快速生长期,一直呈直线增长趋势,生长稳定,到第18年时,生长开始减慢,说明树高生长开始向数量成熟龄过度,线性、幂指数、二次曲线都拟合较好,拟合最好的是二次曲线,拟合优度R2=0.998 3。经对第8、第9两组树高生长量数据根据公式计算预测值,然后和实际测量值进行相对误差检验(详见表3),幂指数拟合公式预测精度高,相对误差均小于0.04,综合拟合优度最大和数据验证的相对误差最小,确定树高总生长量数学模型最佳应为:
H=2.939 2a0.745 9R2=0.995
上式中H表示树高总生长量,a表示树木年龄。

图9 树高线性拟合

图10 树高幂指数拟合

图11 树高二次曲线拟合
图12 树高对数拟合

编号实际值线性公式预测值相对误差幂指数公式预测值相对误差二次曲线公式预测值相对误差对数公式预测值相对误差824.1024.670.0223.250.0424.970.0420.810.14924.6027.460.1225.380.0327.970.1421.800.11
3 讨论
综上分析,经过拟合优度和数据验证相对误差比较,18年生三倍体毛白杨材积总生长量数学模型最佳应为:V=0.000 9a2.318,R2=0.996 8(式中V表示材积总生长量,a表示树木年龄)胸径总生长量数学模型最佳应:D=-0.018 6a2+1.914 5a+0.194 3,R2=0.998 7(式中D表示胸径总生长量,a表示树木年龄);树高总生长量数学模型最佳应为:H=2.939 2a0.745 9R2=0.995(式中H表示树高总生长量,a表示树木年龄)。
胸径、树高总生长量在18年前近似线性增长,并一直处于快速增长期,说明三倍体毛白杨缓苗快,生长旺盛,未达到数量成熟龄,材积总生长量呈曲线增长,在前4年生长缓慢,第4年后进入快速增长趋势,到第18年时,生长开始减慢,说明三倍体毛白杨前18年处于幼林阶段,在这个生长阶段,其总生长量数学模型采用幂指数和二次曲线拟合较好,故幼林期上述建模精度最高。到第18年生时,树高和材积生长减慢,总生长量趋势于幂指数曲线,开始过渡中龄林阶段,曲线拟合优度虽然高,但数据验证相对误差增大,为此,继续观测调查,今后采用Logistic对三倍体毛白杨全生长期建模分析比较。
[1] 吕士行,方升佐,徐锡增.杨树定向培育技术[M].北京:中国林业出版社,1997.
[2] 康向阳.三倍体毛白杨新品种选育[J].北京林业大学学报,2004,26(3):40,63.
[3] 李广德,富丰珍,席本野,等.基于热扩散技术的三倍体毛白杨单木及林分蒸腾耗水研究[J].生态学报,36(10):2945-2953.
[4] 肖君.南方型杨树人工林生长与收获模型的研究[D].南京:南京林业大学,2006.
[5] 陈昌雄.闽北杉木生长和收获模型的研究[J].福建林学院学报,1995,15(3):223-225.
[6] 刘淑春,张仁福,姜小文,等.湘南引种三倍体毛白杨生长模型研究[J].湖南林业科技,2005,32(5):45-47.
[7] 北京林业大学. 数理统计[M].北京:中国林业出版社,1980.
[8] 韦博成.非线性回归分析及其应用[M].北京:中国统计出版社,1997.
Establishment and Verification of Growth Mathematical Model of TriploidPopulusTomentosa
SHE Sheng-bin, LI Xiao-hua, HUANG Zhi-gang, LI Hai-jun
(ForestryInstituteofHanzhong,Hanzhong,Shaanxi723000)
In order to study the growth rules and to predict growth tendency of triploidPopulusTomentosa, the optimal growth mathematical models based on timber volume, diameter at breast height and tree height were established using linear and nonlinear regression analysis on growth of 18-year-old triploidPopulusTomentosasample trees located in Forestry Institute of Hanzhong. The results showed that the optimal total growth mathematical models werev=0009a2.318for timber volume,D=-0.0186a2+1.9145a+0.1943 for diameter at breast height and :H=2.9392a0.7459for tree height, which provided a scientific basis for predicting growth of triploidPopulusTomentosa.
TriploidPopulusTomentosa; growth model
2016-12-18 作者简介:佘生斌(1975-),男,宁夏彭阳人,本科学历,高级工程师,主要从事林业科研、技术推广等工作。
S711
A
1001-2117(2017)01-0025-04
