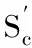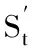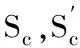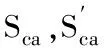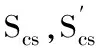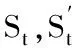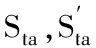浅谈低压储罐在拉压双向力下的罐壁厚度计算及受力特点
2017-04-22梁宏斌
韩 丁 曹 岩 梁宏斌
华陆工程科技有限责任公司 西安 710065
浅谈低压储罐在拉压双向力下的罐壁厚度计算及受力特点
韩 丁*曹 岩 梁宏斌
华陆工程科技有限责任公司 西安 710065
针对API620低压储罐在拉压双应力下的储罐厚度计算,本文给出一种解析法来与API620标准附录F.2中的图解法进行比较,分析各自的优缺点并讨论拉压双应力下罐体的受力特点。
拉压双向力 解析法 储罐厚度计算
1 低压储罐概述
低压储罐国外常用标准是美国标准API STANDARD 620,其压力适用范围为正压≤103.42kPa,负压≤0.43kPa,温度适用范围为-198~121℃[1]。该标准适用压力较高,在多数情况下,为了减少低沸点储存介质在存储时的蒸发损耗,或避免储液与大气接触而造成氧化的需要,储罐的操作压力就需要提高。随着石油化工工业的发展,低压储罐的使用也逐渐普遍起来[2]。
2 低压罐体壁厚计算
相较于一般的常压或微内压储罐,API620标准适用压力较高,按此标准设计的储罐壁厚较大,又不能按普通的压力容器考虑,所以对该类低压储罐的罐体厚度计算, API620标准引入经向单位力T1和纬向单位力T2的概念,这两个单位力是带有方向的力,单位为N/mm,T1和T2为正值表示拉应力,为负值表示压应力。罐体本身主要包括罐顶、罐壁、承压环及罐底,本文主要讨论罐壁的厚度计算,其中当T1和T2均为正值或均为负值时,厚度计算相对简单,不做论述。在T1为正值,T2为负值或者T1为负值,T2为正值时,厚度计算较为复杂,而且限制条件较多,为本文主要讨论的内容。关于拉压双向力下的罐体壁厚计算,API620中附录F.2例题给出的算法是图解法,本文给出一种解析法来进行壁厚计算并比较两种方法的优缺点,最后对拉压双向力下的罐体受力特点进行简单讨论。
3 在拉压双向力下罐体厚度计算
3.1 API附录图解法
API620附录F.2.1的算例,介绍的是在拉压双向力下运用图解法进行计算的过程。条件:罐壁钢板为ASTM A442 Grade55级,经向单位拉力T1为700.5N/mm,纬向单位压力T2为886.14N/mm,经向的曲率半径R1为1905mm,从壁表面沿法线到回转轴的长度R2为7620mm,罐壁采用双面对接结构,其受拉焊接接头系数E为0.85,腐蚀裕量为1.5875mm,运用图解法求所需最小厚度。API620附录F图F-2见图1。
ASTM A442 Grade55级钢板在纯拉伸时的最大许用拉应力Sts为113.764MPa,由于纬向受压,所以R和R1均为1905mm。
图解法的思路是假设从小到大几个厚度,然后得出对应不同厚度下的(t-c)/R值、Sc值、St值及N值,其中,
在图1中,找出各个厚度的Sc值和其对应的(t-c)/R值,标出其交点,绘出一条平滑的U-U曲线;再以(t-c)/R值及对应的N值的交点,绘出另一条平滑的V-V曲线。
两条曲线的交点对应的(t-c)/R值即为允许的最小值,这个值既满足拉应力限制,也满足压应力限制。查图可知,Sc=Sca=68.95MPa,N≈0.48,由于N值小于焊接接头系数E,所以N取0.48,St=Sta=NSts=0.48×113.764=54.6MPa,由拉力T1可得:
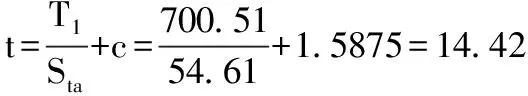
或由压力T2可得:
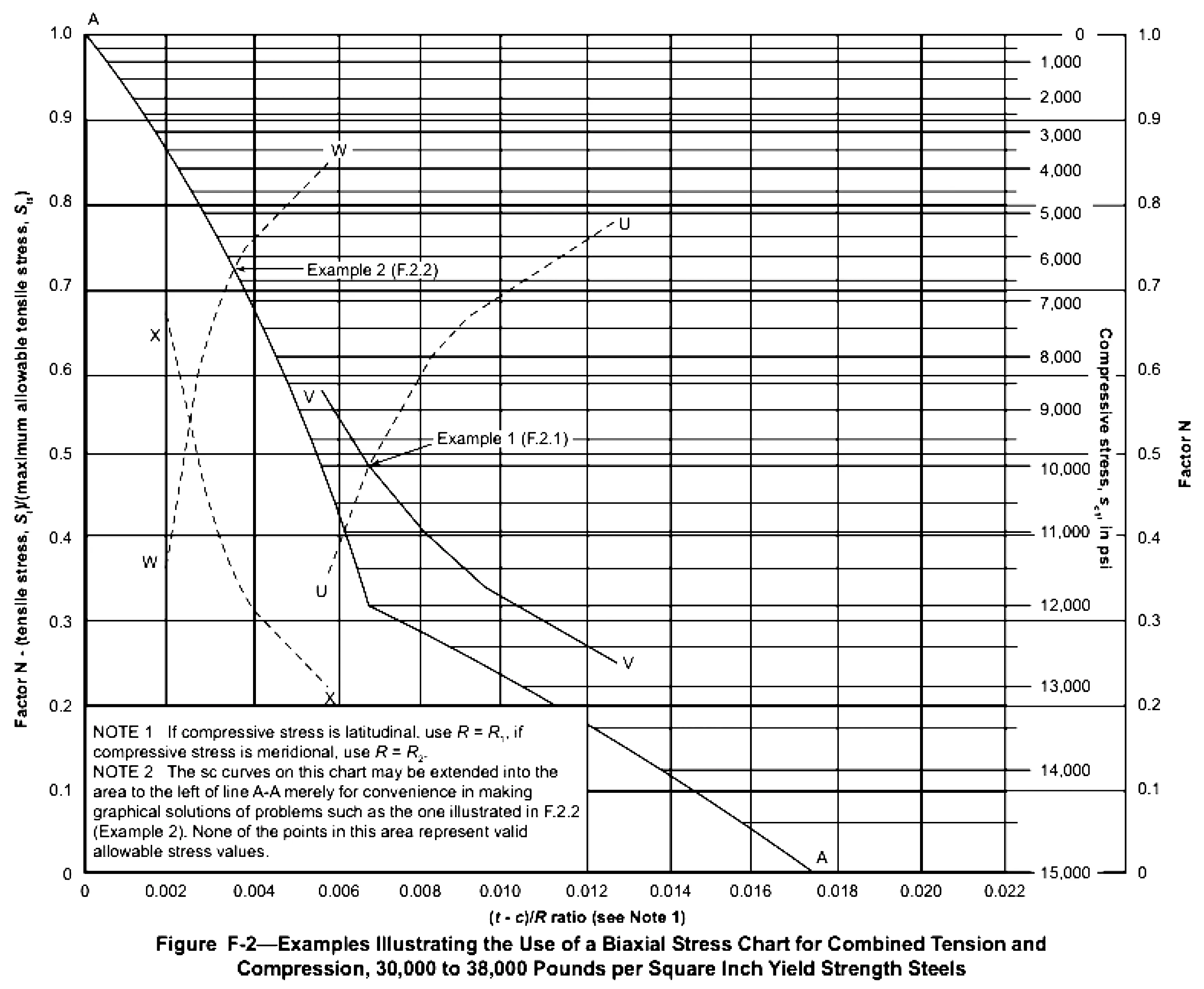
图1 API620附录F图F-2
由于两条曲线交点并没有超出API620附录F中图F-2的A-A曲线,所以该t值符合条件。同时要指出,由于图解法读图取值有一定误差,所以由拉应力和压应力算出的厚度略有不同。
3.2 解析法
本文提出一种解析法计算壁厚,步骤如下:
(1)设定T1为拉应力,T2为压应力(或者T1为压应力,T2为拉应力),然后假定一个壁厚值t,该值既满足拉应力限制,又满足压应力限制,且St=Sta,Sc=Sca,则t值同时满足以下两式:
由上式可得:
又有Sta=NSts,Sca=MScs,即,
(1)
可得:
(2)
API620附录F图F-1见图2。
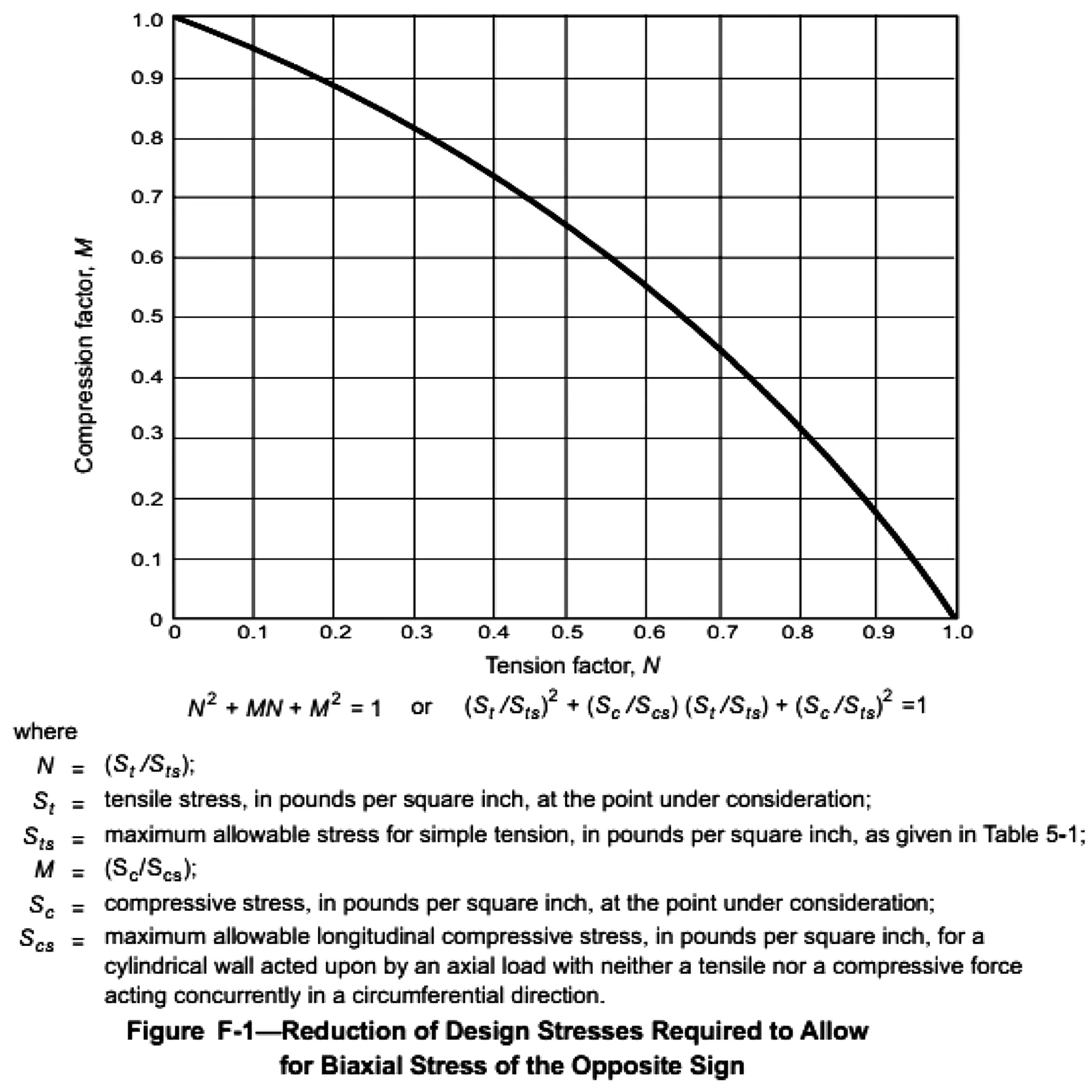
图2 API620附录F图F-1
由图2可知,N和M有以下关系:
N2+MN+M2=1
解析求得:
(3)
将M带入公式(1)可得:
求得:
(4)
这里应当注意到公式(4)的Scs是随着(t-c)/R变化的值,所以假定Scs为定值且取最大值103.42MPa,可得:
(5)
在求得N值的情况下,拉应力下厚度值:
(6)
由N值可求得M值,由公式(1)可知,拉应力下厚度值与压应力下厚度值相同,此时可根据厚度值t、M和N求出:
这里St与Sta相等时,另有:
及此时(t-c)/R对应的Scs值。
如果单位压力T2不超过与它同时存在的相垂直的单位拉力T1的5%时,计算需按照API620中5.5.3.2条的规定确定拉应力的大小(即经向和纬向单位力T1和T2均为拉力,或其中一个为拉力,另一个为零时,计算的拉应力值Stc不应超过API620中表5-1中规定的纯拉伸的最大许用值Sts),那么本节中的假设自然也不成立。但Sta值不应超过API620中表5-2中焊接接头系数与表5-1中许用应力的纯拉伸的最大许用值Sts的乘积(ESts)。
(2)如果此时求得的t值同时满足St≤Sta,Sc≤Scs及Sc≤Sca三个条件,那么该值就是既满足拉应力又满足压应力条件的值。
(3)根据假设可知,St=Sta及Sc=Scs,所以只需验证此时的St≤Sta及Sc≤Scs能否满足条件,如果不能,则按下文进行调整计算。
(4)对于拉应力,St≤Sta这个条件可以通过增大厚度t来确保成立,但是当拉应力T1比压应力T2显著较大的时候,可能会出现很大的N值,此时,当N>E的时候,N值取E值,当N≤E的时候,N值不变,还要注意,如果拉应力T1比压应力T2显著较大的时候,可能会出现较大的壁厚值t,会涉及到材料本身的厚度限制、采购困难以及热处理等一系列问题,因为这时候是拉应力起主要作用,所以可能需要重新选择纯拉伸的最大许用压力Sts更大的材料。
(5)如满足了步骤(3)要求,但是Sc>Scs,在此t值下,拉应力St已经满足要求,而压应力Sc超过了(t-c)/R对应下的最大许用压应力Scs,由于Sc=T2/(t-c),所以需要增大厚度t来降低Sc以确保满足条件Sc≤Scs。另外随着壁厚t的增大,拉应力St=T1/(t-c)值会减小,所以此时压应力是控制值。假设壁厚为t′的时候(此时t′>t),压应力Sc最终达到Sc=Scs,那么压应力Sc=T2/(t′-c)=Scs。
关于Scs的取值,参见图3。当(t′-c)/R不同范围时,Scs的计算方式也不同,说明如下:
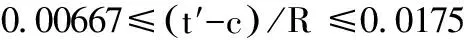
Scs=103.4MPa
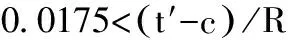
由于限定条件区间为(t′-c)/R<0.00667,那么t′的有效区间为[0,0.00667R+c],此时需要验证t′是否在这个区间,如在,t′值就满足压应力的值,如不在,就继续验证下个条件。
当0.00667≤(t′-c)/R≤0.0175时,t′可得:
由于限定条件区间为0.00667≤(t′-c)/R≤0.0175,那么t′的有效区间为[0.00667R+c, 0.0175R+c],此时需要验证t′是否在这个区间,如在,t′值就是满足压应力的值,如不在,就继续验证下个条件。
当0.0175<(t′-c)/R时,t′可得:
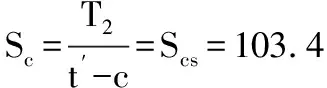
由于限定条件区间为0.0175<(t′-c)/R,那么t′的值大于0.0175R+c,此时需要验证t′是否满足条件,如果不满足,说明压应力过大,结构无法承受。
在求出t′值后,需要验证该值是否满足步骤(2)的其他条件,如果符合,则说明该值就是既满足拉应力又满足压应力条件的值。
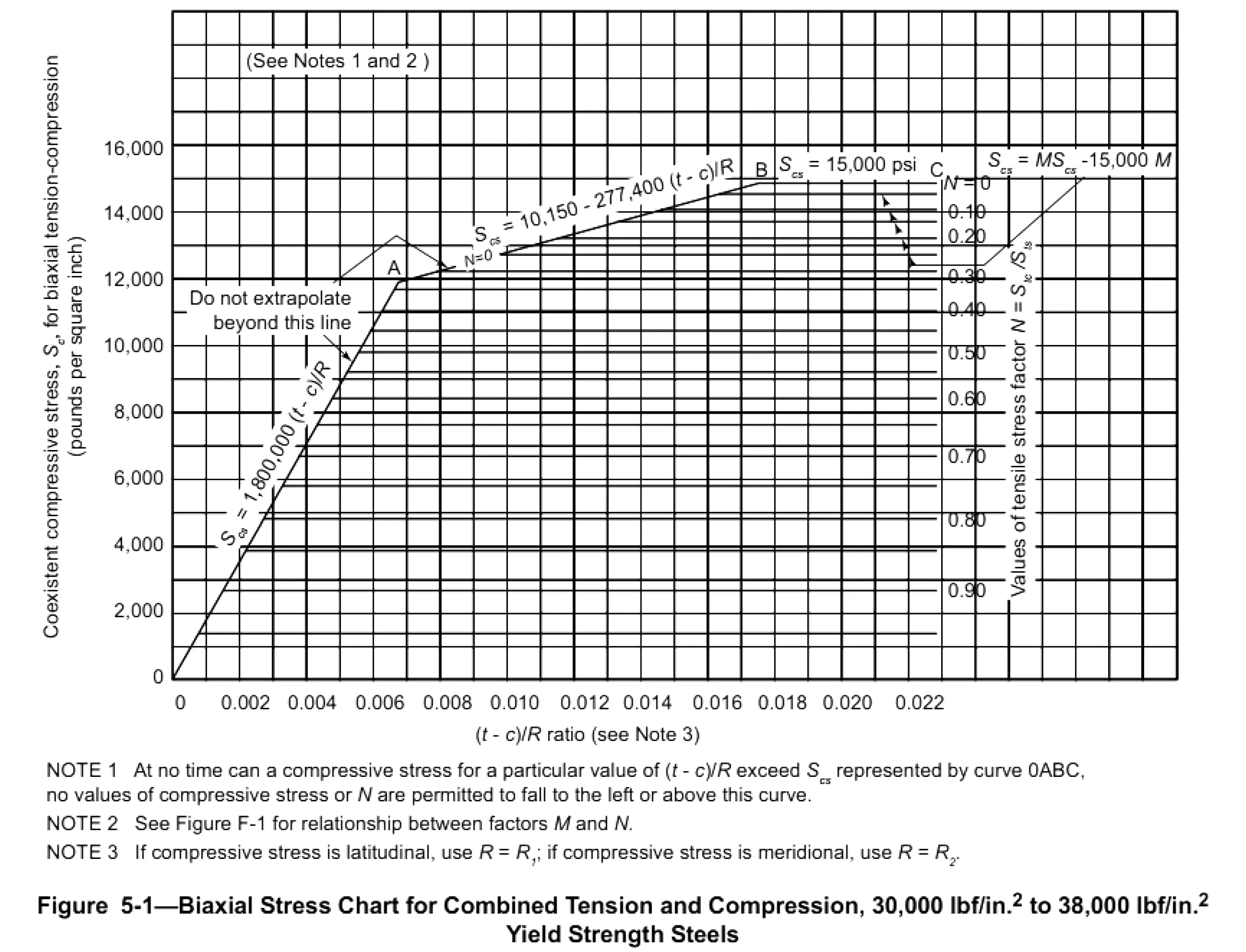
图3 组合拉应力和压应力的双向应力
3.3 用解析法验算例题
下面用解析法验算API620中附录F.2.1之例题,由已知条件可带入公式(4)及(3)可求出N为0.48069,M为0.66889,计算可得Sta和NSts均为54.685MPa。
在拉应力下,计算t得:
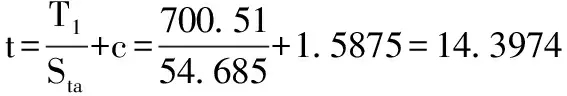
由公式(1)可知,拉应力下厚度值与压应力下厚度值相同。
此时,
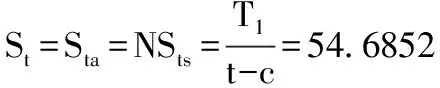
在t为14.3974mm时,(t′-c)/R 为0.00672,所以Scs得:
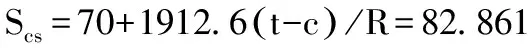
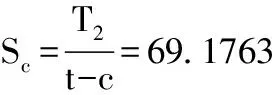
以上结果可见:
Sc=Sca 由上可知该解满足本文中步骤(2)条件,此时t为14.3974mm,既满足拉应力又满足压应力。 这个厚度值下St=Sta,拉应力已经达到最大值,而压应力Sc 若上述F.2.1例题的其他条件不变,只变更T1为400N/mm,同上可得N为0.32569,M为0.79587, Sta和NSts均为37.15MPa。 在拉应力下,计算t得: 由公式(1)可知,拉应力下厚度值与压应力下厚度值相同。 可得: 以上结果可知Sc>Scs。此时压应力超过最大压应力,不满足步骤(2)的条件,壁厚t需要重新计算。 根据步骤(4)假设t′是满足条件的值,那么当(t′-c)/R <0.00667时,计算t′得: 由于限定条件区间为(t′-c)/R <0.00667,那么t′的有效区间为[0,14.29385],所以t′满足要求。 假如继续验证下步骤(4)的后面两个条件:设当t′满足0.00667≤(t′-c)/R ≤0.0175时,计算t′得: 此时t′的有效区间为[14.29385,34.925],可见t′并没有在有效区间上。 当t′满足0.0175<(t′-c)/R时,计算t′得: 此时t′的有效区间为t′>34.925,可见也不满足条件。 下面按照步骤(2)进行验证该解是否满足条件: 即, 可见St 由上可知,t′为13.25mm时,既满足拉应力又满足压应力的解。应当注意,此时的St′ 3.4 两种算法比较 由以上两例可知,图解法和解析法各有优缺点。 (1)图解法的缺点为计算量大(对每个假设的厚度t对应的Sc值、N值及(t′-c)/R值都要进行计算),描点及绘制曲线精度无法保证,查图读值会有误差,不利于计算机进行计算等,优点为可以不借助其它工具通过绘图得出大概厚度值,方便操作等。 (2)解析法的优点在于判断条件清晰,便于理解,而且可通过数学公式及逻辑判断得出高精度的解,并且非常方便的用计算机进行逻辑计算,缺点在于计算公式相对复杂。 对API620而言,由于压力较高,罐壁在罐体材料中占很大比重,所以罐壁的厚度计算非常重要,而拉压应力下的壁厚计算是比较复杂的部分,在计算过程中能求得精确的值很重要,所以分析讨论拉压应力下的厚度计算方法很有意义,而且拉压应力下的罐体受力特点也值得讨论。相对来说,壁厚计算的两种算法各有优劣,但是从精确求解的角度来说,解析法更优,便于理解和判断,也利于计算机编程运算。 符 号 说 明 c 厚度附加量,包括腐蚀裕量和厚度负偏差,mm R1在所考虑的水平面处,在经向平面上罐体的曲率半径,R1与R2在罐体对侧时R1始终为负值,mm R2在所考虑的水平面处,从罐体沿法线至罐中心回转轴的长度,R2始终为正值,mm R 罐壁的曲率半径,当压缩单位力是纬向时,R=R1,当压缩单位力是经向时,R=R2,mm Scc在所考虑的点上,计算的压应力,MPa Stc在所考虑的点上,计算的拉应力,MPa Sts纯拉伸的最大许用应力,MPa T1在所考虑的水平面处,罐壁的经向单位力(在纬向弧度上),受拉时为正值,N/mm T2在所考虑的水平面处,罐壁的纬向单位力(在经向弧度上),受拉时为正值(相似圆筒形罐壁上纬向单位力即是环向单位力),N/mm t,t′罐壁和罐顶的厚度(包括腐蚀裕量),mm 1 API STANDARD 620 2013 (美), Design and Construction of Large, Welded, Low-pressure Storage Tanks[S]. 2 徐 英,杨一凡,朱萍等.球罐和大型储罐[M].北京:化学工业出版社. 2016-12-29) *韩 丁:工程师。2008年毕业于大连理工大学过程装备与控制工程专业。从事压力容器设计工作。联系电话:(029)87989209, E-mail: hd2228@chinahualueng.com。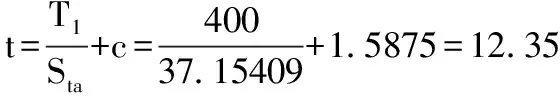
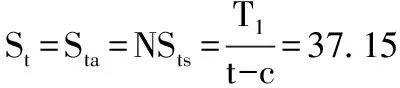
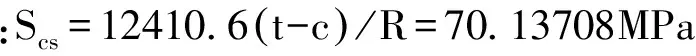
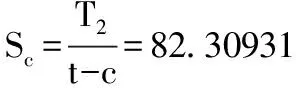
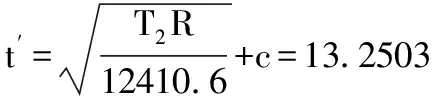

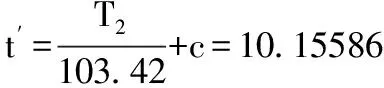
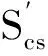
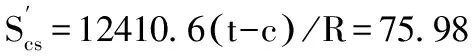
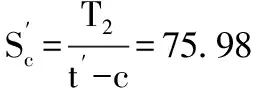
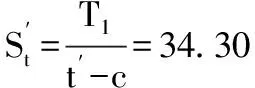

4 拉压双应力下罐体受力特点
5 结语