网格数及体积比对微结构拓扑构型的影响分析
2017-04-21杜大翔杜义贤尹艺峰田启华
杜大翔 杜义贤,2 尹艺峰 周 鹏 田启华
(1. 三峡大学 机械与动力学院, 湖北 宜昌 443002; 2. 水电机械设备设计与维护湖北省重点实验室, 湖北 宜昌 443002)
网格数及体积比对微结构拓扑构型的影响分析
杜大翔1杜义贤1,2尹艺峰1周 鹏1田启华1
(1. 三峡大学 机械与动力学院, 湖北 宜昌 443002; 2. 水电机械设备设计与维护湖北省重点实验室, 湖北 宜昌 443002)
基于拓扑优化理论,采用均匀化方法与能量法,建立了以负泊松比定义为目标函数的优化模型,分别在不同网格数目和不同体积比情况下求解得到相应微结构的二维最优拓扑构型,通过对网格数目及体积比采取控制变量原则,对求解后的拓扑构型结构及迭代次数与目标函数的收敛曲线对比,分析了网格数目及体积比对最优拓扑构型的影响.
微结构; 拓扑优化; 负泊松比; 拓扑构型
1987年由Lakes[1-2]首次制备出了负泊松比泡沫材料,明确提出了负泊松比这一概念,Lakes认为负泊松比现象的产生来自于特殊的元胞形状,能够产生负泊松比的元胞都具有内凹的形状特点,在受到轴向压缩的时候,内凹的部分会产生横向的压缩变形,元胞表现出收缩特性,从而表现出刚度、强度等的增强效应.基于此,很多学者专家对于负泊松比材料的二维微结构展开了研究.Scarpa等[3-4]利用有限元法研究了元胞夹角与内凹六边形等效性能的关系,认为元胞夹角的大小对于负泊松比材料的力学性能有着重要的影响.卢子兴等[5-6]提出了一种综合内凹六边形和正六边形几何特点的二维负泊松比元胞,认为实验制备出的负泊松比泡沫具有不均匀性,并且研究了不同冲击速度下的负泊松比多胞结构的变形和性能,认为在低速冲击过程中负泊松比的效应更加明显.Alderson等[7-9]建立了不同棱边数的手型多胞结构轴向压缩力学模型,认为棱数为4和6的手型结构能产生负泊松比.这些学者研究并给出了具有负泊松比特性的二维拓扑结构,也通过研究发现这类结构呈现负泊松比性质均是因其具有特殊的内凹结构形式的特性,但在理论上并未过多的解释哪些因素直接决定了二维拓扑构型.张卫红、Liang Xia等[10-11]基于能量法和均匀化方法实现了材料微结构的等效弹性性能的预测,并计算得到了具有负泊松比特性的微结构.
因此,本文基于拓扑优化理论[12-13]和能量法[14-15],以负泊松比定义为目标函数建立优化模型.通过对网格数目及体积比采取控制变量法,来确定这两个因素分别对于所求解的最优拓扑构型的影响程度.
1 优化模型的建立及等效弹性系数矩阵的求解
1.1 优化模型的建立
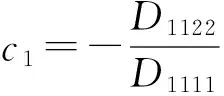
(1)
式中,D1111、D1122分别为等效弹性系数矩阵D沿1方向的弹性模量及由于1方向的伸长应变对2方向产生的弹性模量.V(x)为材料体积,x为设计变量,f为体积比,V0为设计域体积,为避免在优化过程中,单元刚度矩阵出现奇异,取δmin=0.001.
1.2 等效弹性系数矩阵D求解
基于均匀化方法,在微观下的非均质结构可以等效为在宏观下的均质结构,其等效形式如图(1)所示.

图1 微结构等效示意图
所对应的初始等效公式为:
(2)
式中,Y为单胞体积,xkl为载荷kl在周期性单胞体Y允许范围内的位移场,便于数值计算,单体应变能可以表示为:
(3)

由材料力学中胡克定律:

(4)
公式(3)可进一步表示为:
(5)
结合公式(3)、(5),在已知平均应变ε情况下,可以求解得到对应的4种不同情况下的应变能E,即



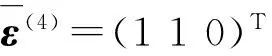
进一步得到的二维负泊松比材料微结构等效弹性系数矩阵D:
(6)
2 敏度分析
目标函数c1对设计变量x求一阶导数,即
(7)
结合有限元方程:
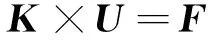
(8)
式中,K为单元刚度矩阵,F、U分别为微结构的结点力向量与结点位移向量.
基于能量法,微结构的等效应变能通式可以表示为:
(9)
式中,n表示上述4种不同的情况,n=1,2,3,4.
由公式(8)、(9)可得微结构的应变能对设计变量x求导:
(10)
其中
(11)
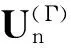
由公式(6)、(9)、(10)可得:
(12)
式中,p为惩罚因子.
综上,二维负泊松比材料微结构等效弹性系数矩阵的敏度分析可以表示为:
(13)
结合有限元分析,通过敏度分析、OC优化准则,可对上述所建立的优化模型求解.
3 数值算例
根据上述构建的优化模型,基于能量法与拓扑优化理论,选取实体材料的弹性模量E0=2.1×105N/mm2,泊松比μ=0.3,在体积比分别取f=0.2、0.4、0.6、0.8,网格数目分别取N=40×40、100×100、150×150求解得到对应微结构最优拓扑构型,具体结果见表1(表1中最优拓扑构型图中黑色表示实体材料部分,白色表示孔洞部分),目标函数c1与迭代次数收敛曲线如图2所示.
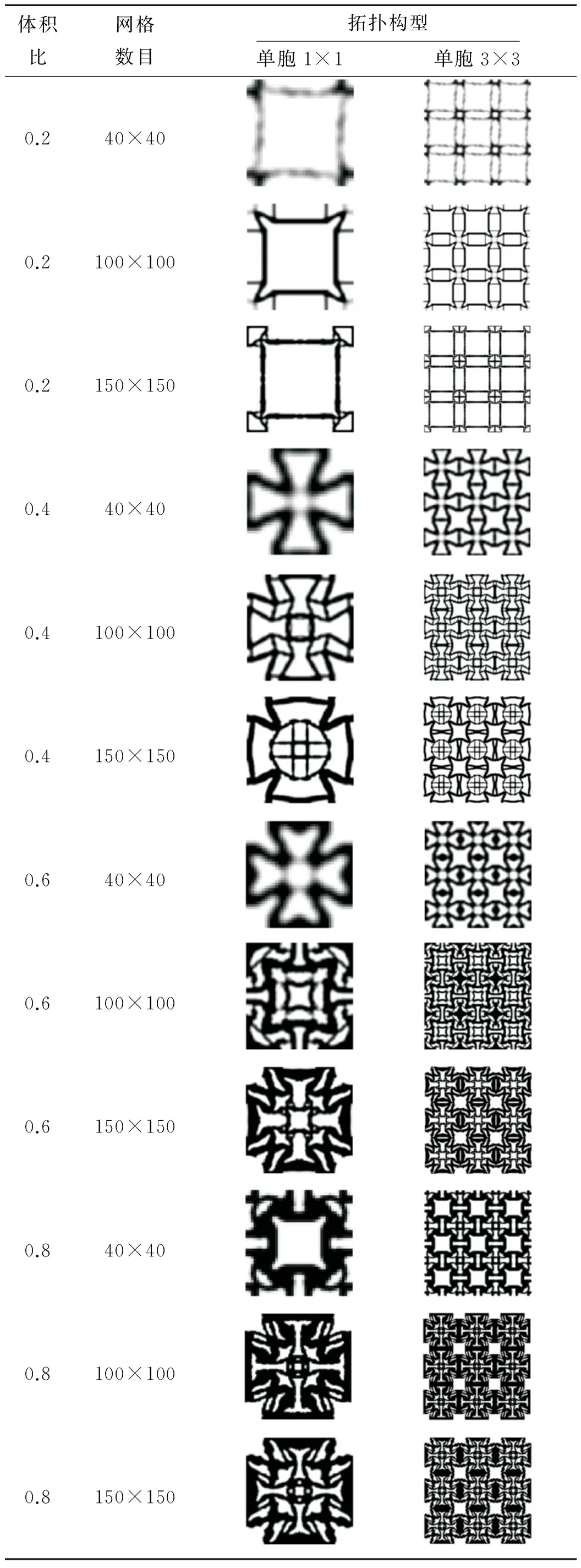
表1 不同情况下微结构的最优拓扑构型

图2 材料体积比0.2、0.4、0.6、0.8时不同网格数目下的目标函数值收敛曲线
算例分析:
1)由表2可知,同一材料体积比(除体积比为0.6时网格数目N=40×40与网格数目N=100×100,150×150在拓扑结构上有较大差异)最优拓扑构型在结构上有相似性,且网格数目越大,拓扑构型越精细.体积比为0.2得到的拓扑构型太稀疏可能导致拓扑构型的不连续性,而体积比为0.8得到的拓扑构型太浓密,在满足结构力学性能要求的同时,耗材过大.
2)由图2可知,材料体积比为0.2的目标函数收敛后不稳定有轻微的振荡,材料体积比为0.4、0.6、0.8的目标函数收敛后基本保持稳定.
4 结 论
本文基于拓扑优化理论和能量法,建立了以泊松比定义为目标函数的优化模型,从算例分析可得,体积比在最优拓扑构型上有较大影响而网格数目主要决定了拓扑构型的精细程度,且体积比的选择在0.4~0.6范围时,既不会影响拓扑构型的连续性也不会导致耗材过大.
[1] Lakes R S, Katz J L, Sternstein S S. Viscoelastic Properties of Wet Cortical Bone—I. Torsional and Biaxial Studies[J].Journal of Biomechanics, 1979, 12(9):657-78.
[2] Greaves G N, Greer A L, Lakes R S, et al. Poisson's Ratio and Modern Materials[J].Nature Materials, 2011, 10(11):823-37.
[3] Scarpa F, Panayiotou P, Tomlinson G. Numerical and Experimental Uniaxial Loading on In-plane Auxetic Honeycombs[J].Journal of Strain Analysis for Engineering Design, 2000, 35(5):383-388.
[4] Miller W, Smith C W, Scarpa F, et al. Flatwise Buckling Optimization of Hexachiral and Tetrachiral Honeycombs[J].Composites Science & Technology, 2010, 70(7):1049-1056.
[5] 卢子兴, 李 康. 四边手性蜂窝动态压溃行为的数值模拟[J].爆炸与冲击, 2014, 34(2):181-187.
[6] 卢子兴, 赵亚斌. 一种有负泊松比效应的二维多胞材料力学模型[J].北京航空航天大学学报, 2006, 32(5):594-597.
[7] Alderson A, Evans K E. Molecular Origin of Auxetic Behavior in Tetrahedral Framework Silicates[J].Physical Review Letters, 2002, 89(22):78-87.
[8] Kocer C, Mckenzie D R, Bilek M M. Elastic Properties of a Material Composed of Alternating Layers of Negative and Positive Poisson's Ratio[J].Materials Science & Engineering A, 2009, 505(1-2):111-115.
[9] Alderson A, Alderson K L, Attard D, et al. Elastic Constants of 3-, 4- and 6-connected Chiral and Anti-chiral Honeycombs Subject to Uniaxial In-plane Loading[J].Composites Science & Technology, 2010, 70(7):1042-1048.[10] Zhang W, Sun S. Scale-related Topology Optimization of Cellular Materials and Structures[J].International Journal for Numerical Methods in Engineering, 2006, 68(9):993-1011.
[11] Liang X, Breitkopf P. Design of Materials Using Topology Optimization and Energy-based Homogenization Approach in Matlab[J].Structural & Multidisciplinary Optimization, 2015, 52(6):1229-1241.
[12] 杜义贤,严双桥,周俊雄,等. 数控插齿机床身的静动多目标拓扑优化设计[J].机械设计,2014,31(29606):64-67.
[13] 张 严,杜义贤,杜大翔,等.极限弹性性能的材料微结构拓扑优化设计[J].三峡大学学报(自然科学版),2016,38(2):71-74.
[14] Bassir H. Using Strain Energy-based Prediction of Effective Elastic Properties in Topology Optimization of Material Microstructures[J]. Acta Mechanica Sinica, 2007, 23(1):77-89.
[15] 戴高明, 张卫红. 周期性多孔材料等效杨氏模量的尺度效应研究[J].中国科学:物理学 力学 天文学, 2009(7):955-963.
[责任编辑 张 莉]
Analysis of Influence of Mesh Number and Volume Ratio on Microstructure Topological Configuration
Du Daxiang1Du Yixian1,2YinYifeng1Zhou Peng1Tian Qihua1
(1. College of Mechanical & Power Engineering, China Three Gorges Univ., Yichang, 443002,2. Hubei Key Laboratory of Hydroelectric Machinery Design & Maintenance, China Three Gorges Univ., Yichang, 443002)
Based on the topology optimization theory, the homogenization method and the energy method are used, an optimization model with negative Poisson's ratio as the objective function is established. The two-dimensional topological configurations of the corresponding microstructures are obtained under different mesh numbers and different volume ratios. The principle of control variables is adopted for mesh numbers and volume ratios, through the comparison of the corresponding topological structure and the convergence curves between the number of iterations and the objective function, the influences of mesh number and volume ratio on microstructure topological configuration are analyzed.
microstructure; topology optimization; negative Poisson's ratio; topological configuration
2016-11-29
湖北省教育厅科学研究计划资助项目(D20161205)
杜义贤(1978-),男,副教授,博士,研究方向为CAD/CAM技术,结构优化与分析.E-mail:duyixian@aliyun.com
10.13393/j.cnki.issn.1672-948X.2017.02.019
TH122:TB34
A
1672-948X(2017)02-0089-04
