不同填土高度下壁厚对钢波纹管力学性状影响

王 洋 洪宝宁 刘 鑫 潘 忱

(1. 河海大学 岩土力学与堤坝工程教育部重点实验室，南京 210098；2. 河海大学 江苏省岩土工程技术工程研究中心，南京 210098；3. 河海大学 隧道与城市轨道工程研究所，南京 210098；4. 江苏省岩土工程公司，南京 210002)

不同填土高度下壁厚对钢波纹管力学性状影响

王 洋1，2洪宝宁1，2刘 鑫1，3潘 忱4

(1. 河海大学 岩土力学与堤坝工程教育部重点实验室，南京 210098；2. 河海大学 江苏省岩土工程技术工程研究中心，南京 210098；3. 河海大学 隧道与城市轨道工程研究所，南京 210098；4. 江苏省岩土工程公司，南京 210002)

通过建立模拟施工条件的数值计算模型，研究不同填土高度下壁厚对钢波纹管变形和力学性能的影响．研究结果表明：填土高度小于8 m时，壁厚对钢波纹管管中处竖向变形量影响较小，壁厚超过4 mm，每增加1 mm变形减小低于0.3%；填土高度大于8 m后，随着壁厚的增加，钢波纹管管中处竖向变形量线性减小，但减幅较小．

钢波纹管； 竖向变形； 轴向应力

钢波纹管涵是由波纹状管或波纹状弧形板通过连接、拼装形成的一种涵洞形式[1]．波纹管结构接近于理想的地下结构，安装后的波纹管既柔韧又结拱成形，其周围回填后形成一个拱形结构和一个弹性层，这个弹性层不断地均衡地下压力[2]．钢波纹管涵具有适应变形能力强、自重轻、运输方便、施工简便、施工工期短且造价低的优点[3-4]．自20世纪50年代在青藏公路中开始使用以来，由于使用状况良好，钢波纹管的应用越来越广[5]．随着钢波纹涵的广泛使用，也出现了严重变形、裂缝、漏水、涵洞积水等情况[6]．目前关于钢波纹管的研究主要集中于现场实验数据分析，而关于钢波纹管数值分析相关研究很少．通过应用有限元软件ABAQUS建立模拟施工条件的数值计算模型，研究不同填土高度下壁厚对钢波纹管变形和力学性能的影响，为钢波纹管涵的设计、施工提供一定理论参考．

1 模型建立

计算模型以二广高速公路连州至怀集段为工程背景，对钢波纹管涵洞进行模型建立和计算结果分析．

1.1 模型尺寸与断面设置

路堤填筑高度为H，钢波纹管涵孔径为D，由于模型尺寸对计算结果具有一定影响[7]，取坡脚至左侧边界距离为1.5H，地基深度为H，模型厚度取5D．模型中钢波纹管涵回填压实范围为，管顶和管底各0.5 m，管身两侧为1.5 m；钢波纹管涵上方覆土高度为20 m，路堤分三级放坡，一、二级放坡坡率1∶1.75，三级放坡坡率1∶1.5，二、三级路堤坡高8 m，路面宽度30 m.为简化计算，取路堤半幅进行模型计算．计算模型中，变形量研究从管口向管中方向每4 m取一个点对管身竖向和水平向变形量情况进行整体研究，选取距管口23 m位置(断面A-A)和管中位置(断面B-B)进行环向和轴向应力研究，应力研究从管顶开始每15°选取一个观测点进行环向和轴向应力的研究．模型尺寸如图1所示，钢波纹管观测断面如图2所示，观测点的选取示意图如图3所示．

图1 模型尺寸示意图

图2 模型观测断面示意图

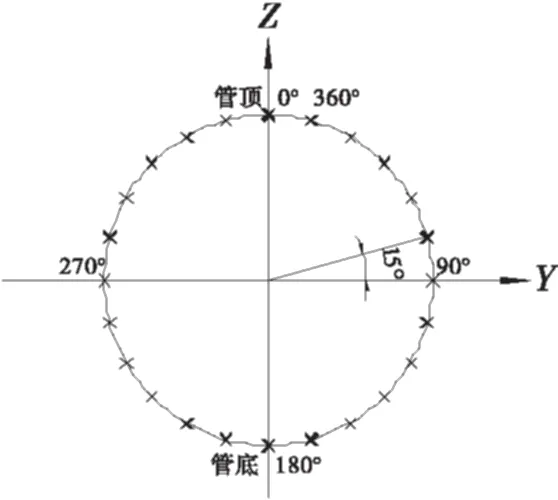
图3 观测点示意图

1.2 模型单元的选取

为达到计算精度，钢波纹管的单元形状取四边形，钢波纹管单元类型取S4R(四节点四边形有限薄膜应变线性减缩积分壳单元)，土体单元类型取C3D8R(八节点六面体线性减缩积分单元)．钢波纹管和与其接触的土体上的单元划分较为精细，远离管的土体单元划分较为粗糙．路堤和钢波纹管单元分别见图4、5．

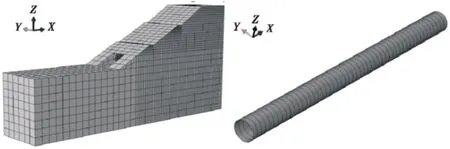
图4 路堤单元划分 图5 钢波纹管单元划分

1.3 波形结构简化

在研究钢波纹管涵时，重点关注管涵环力学和变形特性，因此，模型简化采用环向抗弯刚度等效的方法．钢波纹管波纹形状如图6所示．

图6 波纹形状示意图

在一个波长范围内，通过对波纹截面积分来计算面积和惯性矩，再转化成单位长度内的面积和惯性矩．由于波纹形状具有对称性，故只需对1/4波长进行积分．

1/4波长范围内曲线方程为：

(1)

单位长度面积：

(2)

单位长度惯性矩：

(3)

式中，θ为圆弧段角度的一半；R为圆弧半径；a为直线段在X轴投影长度的一半；t为钢波纹板壁厚．

为了验证该计算方法的精确性，现以美国ASTM[8]规范中152×51 mm波纹钢板为例，对其单位长度截面积和单位长度惯性矩进行计算．计算结果和规范值的比较见表1．从表1可以看出，计算值与规范值误差在0.3%之内，即该计算方法具有很高的精确性，可以作为计算模型简化依据．

表1 计算值与规范值比较

1.4 计算方案和参数

考虑到波纹管壁厚、管径和填土高度等影响因素．计算工况和参数分别见表2～3．

表2 钢波纹管涵洞计算工况

表3 模型计算参数

管径和壁厚取值范围参照二广高速公路实际工况，计算时利用ABAQUS软件中的生死单元功能模拟施工中的填筑过程，为简化计算将波纹管上方填土分为20层，即每层填筑高度为1 m．为了方便计算结果的分析，分别取填土高度4 m、8 m、12 m、16 m和20 m进行分析．数值计算中的材料参数依据工程实际和工程经验进行选取．

2 钢波纹管涵洞变形特性分析

2.1 壁厚对钢波纹管变形的影响

不同填土高度下，管径6 m，壁厚分别为4 mm、5 mm、6 mm和7 mm时钢波纹管涵洞在A-A和B-B断面的变形量如图7～8所示．其中图7表示的是A-A断面钢波纹管涵洞竖向变形量的变化规律，图8表示的B-B断面钢波纹管涵洞竖向变形量的变化规律．图中，纵坐标中的变形量为钢波纹管变形后的管径与初始管径的差值(下同)．

图7 A-A断面竖向变形量变形规律

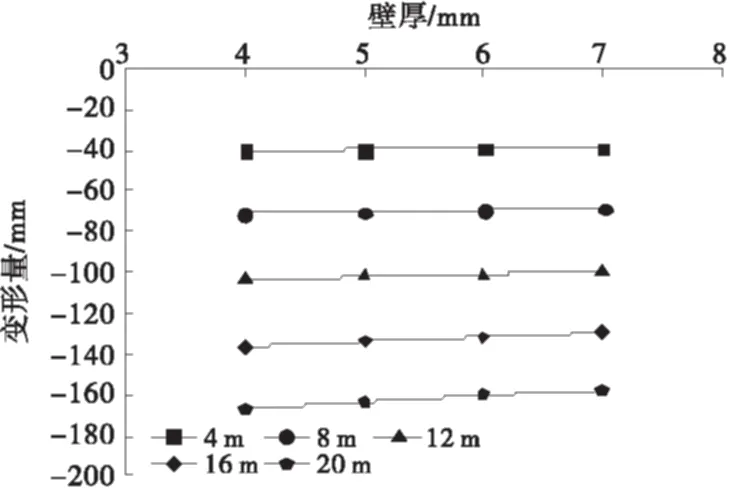
图8 B-B断面竖向变形规律

分析图7～8可以看出，填土高度小于8 m时，壁厚对钢波纹管管中处竖向变形量影响较小；填土高度大于8 m后，随着壁厚的增加，钢波纹管管中处竖向变形量线性减小，但减幅较小．如当填土高度20 m时，钢波纹管在壁厚为4 mm和7 mm时最大竖向变形量分别为166.6 mm和157.5 mm，减幅为5.8%．

2.2 壁厚对钢波纹管环向应力的影响

不同填土高度下，管径为6 m，壁厚分别为4 mm和7 mm时A-A断面和B-B断面钢波纹管环向应力变化规律如图9～12所示．在不同填土高度下，管径为6 m，壁厚分别为4 mm、5 mm、6 mm和7 mm时A-A断面和B-B断面0°位置环向应力变化规律如图13～14所示．

图9 t=4 mm时A-A断面环向应力变化规律

图10 t=4 mm时B-B断面环向应力变化规律

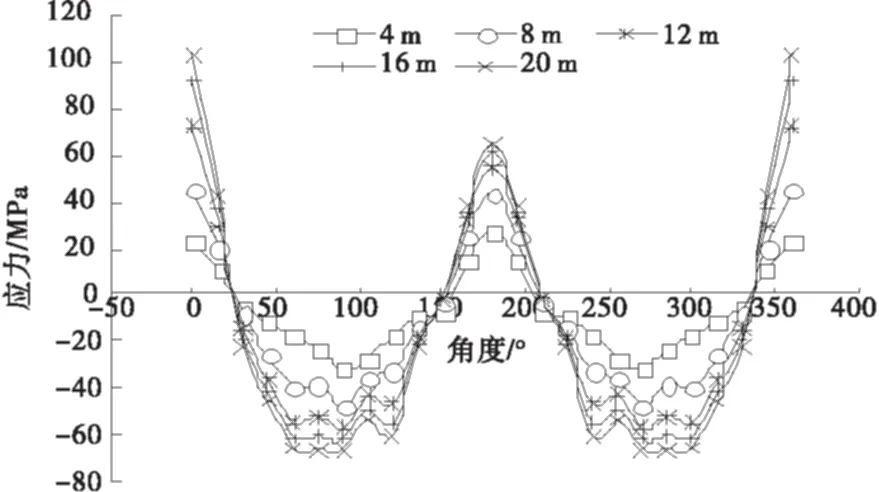
图11 t=7 mm时A-A断面环向应力变化规律

图12 t=7 mm时B-B断面环向应力变化规律

图13 A-A断面0°位置环向应力变化规律

图14 B-B断面0°位置环向应力变化规律

分析图9～12可以看出随着填土高度的增加，断面上各点环向应力也相应增加，且环向应力沿着过圆管中心的垂直轴线对称分布．现以钢波纹管半幅进行分析，0°～180°范围内拉、压应力不断转换；A-A断面最大拉应力出现在0°位置(管顶)，最大压应力出现在90°位置，B-B断面最大拉应力出现在0°位置，最大压应力出现在60°位置．

分析图13、14可以看出A-A断面0°位置环向应力随着壁厚的增加而增加，增幅较小．当填土高度较小时，B-B断面0°位置环向应力受壁厚的影响较小；当填土高度较大时，随着壁厚的增加，B-B断面0°位置环向应力少量减小．钢波纹管属于柔性结构，增加壁厚一定程度上相当于将钢波纹管的柔性特性向刚性特性转化，变形能力减小，导致管身部分位置出现应力增加的情况．以填土高度20 m为例，钢波纹管在壁厚为4 mm和7 mm时A-A断面环向拉应力值分别为97.2 MPa和102.8 MPa，增幅为5.4%；B-B断面环向拉应力值分别为203.0 MPa和194.8 MPa，减幅为4.2%，环向压应力值分别为-104.3 MPa和-119.7 MPa，增幅为12.9%．环向应力最大值小于其屈服强度值345 MPa．

2.3 壁厚对钢波纹管轴向应力的影响

不同填土高度下，管径为6 m，壁厚分别为4 mm和7 mm时钢波纹管轴向应力变化规律如图15～18所示．在不同填土高度下，管径为6 m，壁厚分别为4 mm、5 mm、6 mm和7 mm时A-A断面和B-B断面180°位置环向应力变化规律如图19～20所示．

图15 t=4 mm时A-A断面轴向应力变化规律

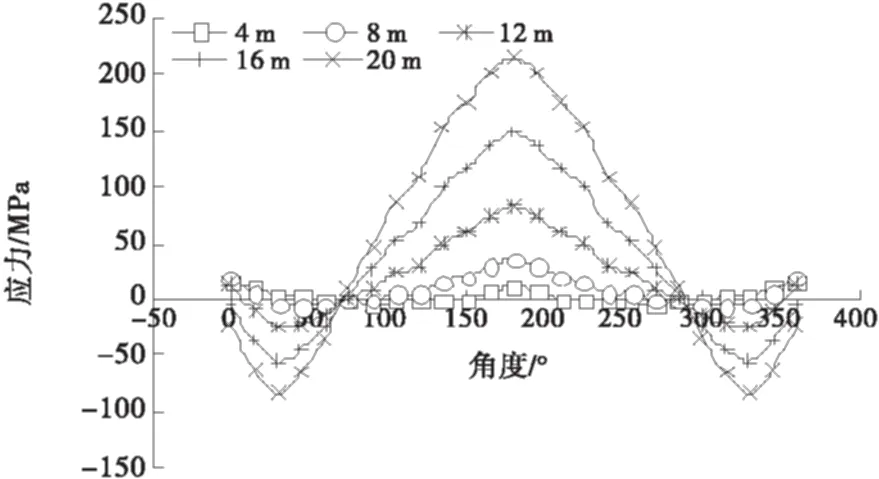
图16 t=4 mm时B-B断面轴向应力变化规律

图17 t=7 mm时A-A断面轴向应力变化规律

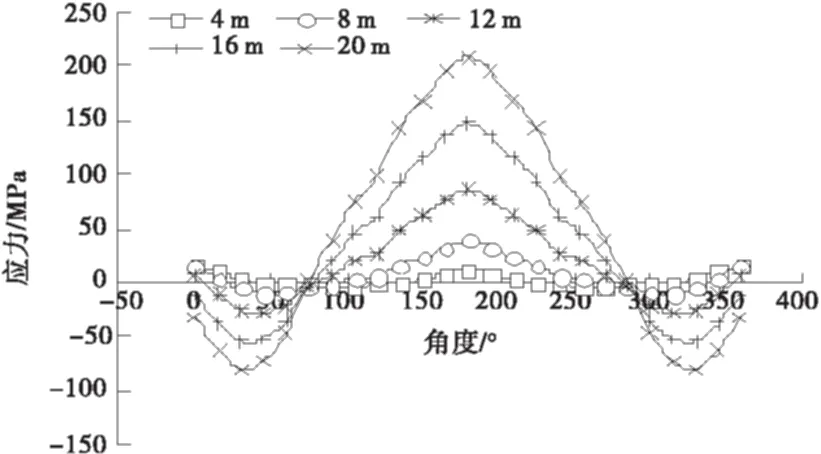
图18 t=7 mm时B-B断面轴向应力变化规律

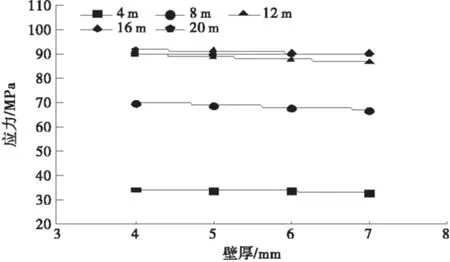
图19 A-A断面180°位置轴向应力变化规律

图20 B-B断面180°位置轴向应力变化规律

分析图15～18可以看出随着填土高度的增加，断面上各点轴向应力也相应增加，且轴向应力沿着过圆管中心的垂直轴线对称分布．现以钢波纹管半幅进行分析，0°～180°范围内拉、压应力不断转换；0～90°范围内所受轴向应力为压应力，压应力随着角度的增大先增大后减小，断面30°位置处压应力最大；90°～180°范围内所受轴向应力为拉应力，拉应力随着角度的增大而增大，断面180°位置处(管底)拉应力最大．

2)A-A断面180°位置轴向应力随着壁厚的增加少量减小．当填土高度较小时，B-B断面180°位置轴向应力受壁厚的影响较小；当填土高度较大时，B-B断面180°位置轴向应力随着壁厚的增加少量减小．

3 结 论

1)填土较高时，壁厚对钢波纹管竖向变形量有一定的影响，且竖向变形量随着壁厚的增加线性减小．

2)填土高度小于12 m时，壁厚对钢波纹管涵洞环向应力影响很小．当填土高度超过12 m时，壁厚的增加导致涵管环向应力线性变化．

3)不同填土高度下，随着壁厚的增加，钢波纹管轴向应力相应减小，但减幅较小，壁厚每增加1 mm轴向应力减小小于1.8%．说明壁厚对钢波纹管圆周断面上轴向应力变化影响较小．

[1] 李晓勇，梁养辉，李祝龙，等．低路堤荷载作用下钢波纹管涵切向应变现场测试[J]．公路工程，2013，38(3)：90-94，125．

[2] 粟 缤．波纹管涵受力性能数值分析[D]．北京：北京交通大学，2009．

[3] 潘 忱，洪宝宁，刘 鑫，等．不同填土高度下钢波纹管变形与力学性状的数值分析[J]．河南科学，2014，32(11)：2281-2286．

[4] 王军刚，刘 强．钢波纹管涵在山区高速公路中的应用[J]．中外公路，2009，29(2)：165-168．

[5] 刘 戈，符 进，章金钊．多年冻土地区金属波纹管涵设计[J]．公路，2008，9(9)：316-318．

[6] 李晓勇，梁养辉，李祝龙，等．低路堤荷载作用下钢波纹管涵切向应变现场测试[J]．公路工程，2013，38(3)：90-94，125．

[7] 张鲁渝，郑颖人，赵尚毅，等．有限元强度折减系数法计算土坡稳定安全系数的精度研究[J]．水利学报，2003(1)：21-27．

[8] ASTM-A796/A 796M,1999 Standard Practice for Structural Design of Corrugated Steel Pipe, Pipe-Arches, and Arches for Storm and Sanitary Sewers and Other Buried Applications[S]． West Conshohocken PA 19428-2959．

[责任编辑 王康平]

Numerical Analysis of Mechanical and Deformation Properties of Steel Corrugated Pipe with Different Thicknesses under Different Embankment Heights

Wang Yang1,2Hong Baoning1,2Liu Xin1,3Pan Chen4

(1. Key Laboratory of Ministry of Education for Geomechanics & Embankment Engineering, Hohai Univ., Nanjing 210098, China; 2. Jiangsu Research Center for Geotechnical Engineering Technology, Hohai Univ., Nanjing 210098, China; 3. Tunnel and Underground Engineering Institute, Hohai Univ., Nanjing 210098, China; 4. Jiangsu Geotechnical Engineering Company, Hohai Univ., Nanjing 210002, China)

By setting up a numerical model to simulate the conditions of construction to research how the different wall thicknesses of steel corrugated pipe effect the deformation and mechanical properties of the steel corrugated pipe under different embankment heights. The results show that： when embankment height is less than 8 m, the thickness of the steel corrugated pipe has little effect on the vertical deformation; when the thickness of steel corrugated pipe is more than 4 mm, the decrease of vertical deformation caused by each 1 mm wall thickness increase is less than 0.3%; when the filling height of more than 8 m, along with increasing the thickness of the steel corrugated pipe, the vertical deformation decreases linearly; but the decrease is small.

steel corrugated culvert pipe; vertical deformation; axial stress

2016-09-06

江苏省自然科学基金青年基金(BK20140848); 广东省交通运输厅科技项目(科技-2015-02-013，科技-2015-02-015)

王 洋(1993-)，男，硕士，从事软基处理方面研究．E-mail：1595786176@qq.com

10.13393/j.cnki.issn.1672-948X.2017.02.015

TV16

A

1672-948X(2017)02-0069-05