永磁BLDCM双闭环控制系统技术研究
2017-04-21杨振宇
杨振宇
(中国地质工程集团公司 工程部,北京 100093)
永磁BLDCM双闭环控制系统技术研究
杨振宇
(中国地质工程集团公司 工程部,北京 100093)
针对永磁无刷直流电机开环控制误差大,以及单闭环控制动静态特性差的缺点,研究了双闭环控制系统。文中介绍了永磁无刷直流电动机PWM调速的工作原理,阐述了其双闭环控制系统的设计过程,推断了电流调速器和转速调速器的数学模型。仿真结果验证了永磁无刷直流电机双闭环控制具有良好的动静态特性。
无刷直流电机;PWM控制;双闭环控制;建模
在实际应用中,直流电机已由过去简单的起停控制、提供动力为目的的应用,上升到对其速度、位置、转矩等进行精确的控制,使被驱动的机械运动符合预想的要求。例如在工业自动化、办公自动化和家庭住宅自动化方面使用的大量电机,基本都采用功率器件进行控制,将预定的控制方案、规划指令转变成期望的机械运动。这种新型控制技术已不是传统的“电机控制”和“电气传动” 而是“运动控制”。运动控制使被控机械运动实现精确的位置控制、速度控制、加速度控制、转矩或力的控制,以及这些被控机械量的综合控制[1-2]。因此,对永磁无刷直流电动机控制性能的研究是今后研究的热点。本文针对永磁无刷直流电机开环控制的误差较大,以及单闭环控制动静态较差的问题,研究了其双闭环控制技术。
1 永磁无刷直电机的调速原理
根据文献[3~4]可知,永磁无刷直流电机转子相对于定子的机械角速度公式为
(1)
因此,可以通过改变电枢电压U的大小来调节电机的角速度。而改变电枢电压U的方法主要是采用脉宽调制技术即PWM(Pulse Width Modulation)控制技术。图1(a)为直流斩波器—电动机系统的原理图,其中用开关符号VT表示任何一种电力电子开关器件;VD表示续流二极管。当VT导通时,直流电源电压U加到电动机上;当VT关断时,直流电源与电动机断开,电动机电感经VD续流,两端电压接近于零。如此反复,得到电枢端电压波形u=f(t),如图2(b)所示。这样,电动机得到平均电压
(2)
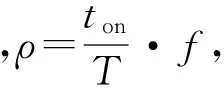

图1 直流斩波器-电动机系统原理和电压波形
由此可见,要通过改变电机的电枢电压来调速,只需改变功率开关器件的占空比即可,这就是脉宽调制技术的调速原理。
2 永磁无刷直流电机双闭环控制系统
工程设计中常采用转速、电流双闭环来对电机进行调速,其双闭环调速系统的动态结构如图2所示[5-7]。它包括电流调节器ACR、电压调节器ASR、电流滤波与转速滤波等多个环节,而电力电子装置用一阶惯性环节代替。由于电流检测信号中含有交流分量,为不使它影响到调节器的输入,需加低通滤波,其滤波时间常数用Toi表示,为平衡这个滤波环节所引起的延迟,在给定信号通道上加入一个同等时间常数的滤波环节,称作给定滤波环节。同理,在转速环中也加入滤波环节,其滤波时间常数用Ton来表示,并在转速给定通道上也加入时间常数为Ton的给定滤波环节。这样就可以方便地设计电流调节器和转速调节器了。

图2 双闭环调速系统的动态结构图
2.1 电流调节器的设计
在图2所示的电流环中,反电动势与电流反馈的作用相互交叉,给设计带来麻烦。但由于反电动势与转速成正比,而转速的变化往往比电流的变化慢得多,因此对电流环来说,反电动势是一个变化较慢的扰动,在电流的变化过程中,在一定条件下可以认为反电动势基本不变即ΔE=0,这样,在按动态性能设计电流环时,可以暂不考虑反电动势的影响,也即可以把反电动势的作用去掉,得到电流环的近似结构图,如图3(a)所示。忽略反电动势对电流环作用的近似条件为[8-9]
(3)
式中,ωci为电流环开环频率特性的截止频率。
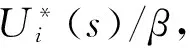
T∑i=Ts+Toi
(4)
这个简化条件为
(3)
需要注意的是,电力电子装置用一阶惯性环节代替的近似条件为
ωci≤1/3Ts
(6)
则电流环结构图最终简化成如图3(c)所示。
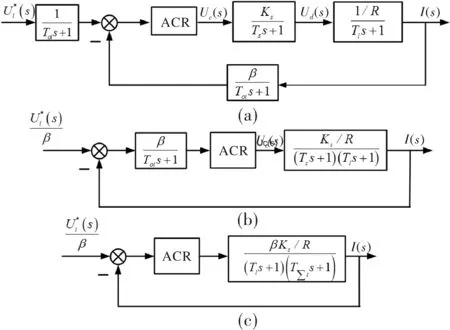
图3 电流环的动态结构图及其化简图
电流调节器采用PI型,把电流环校正成I型系统,其传递函数可以写成[10-11]
(7)
式中,Ki为电流调节器的比例系数;τi为电流调节器的超前时间常数。
使调节器零点与控制对象的大时间常数极点对消,选择
τi=Tl
(8)
则电流环的动态结构框图便成为图4所示的典型形式,其中
(9)

图4 校正后的电流环
由于电流调节器的参数是Ki和τi,τi已经选定,待定的参数只有比例系数Ki,可根据所需要的动态性能指标选取。在一般情况下,希望电流超调量σi≤5%,根据调节器的工程设计方法[12],可选ξ=0.707,KIT∑i=0.5,则
(10)
再由式(8)和式(9)得
(11)
从而可以确定电流调节器的参数。
2.2 转速调节器的设计
为便于转速调节器的设计,先把电流内环进行等效,以使电流环成为转速环中的一个环节。因此先求出电流环的闭环传递函数
(12)
忽略高次项,Wcli(s)可降阶为
(13)
近似条件如下
(14)
式中,ωcn为转速环开环频率特性的截止频率。
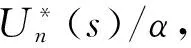
(15)
其近似的条件为
(16)
转速调节器也采用PI型,把转速环校正成典型的Ⅱ型系统,以满足动态抗扰性能好的要求。其传递函数可以写成
(17)
式中,Kn为转速调节器的比例系数;τn为转速调速器的超前时间常数。
这样,调速系统的开环传递函数为
(18)

图5 转速环的动态结构图及其简化图
转速环开环增益KN为
(19)
转速调节器的参数包括Kn和τn,按照典型Ⅱ系统的参数关系,有
τn=hT∑n
(20)
(21)
其中,h为中频宽。因此
(22)
至于中频宽h应选择多少,要看动态性能的要求决定,无特殊要求时一般以选择h=5为好。转速环的截止频率ωcn为
ωcn=KN·τn
(23)
3 Matlab/Simulink仿真
根据前面设计的永磁无刷直流电机双闭环控制系统,在Matlab/Simulink中进行了建模与仿真,仿真结果如图6和图7所示[13-15]。图6为永磁无刷直流电机双闭环控制系统的整个仿真波形,从上至下分别为三相交流电流仿真波形,转矩仿真波形以及角速度仿真波形。从图6可以看出,电机起动时以最大电流恒流起动,角速度按线性关系线性增大;当角速度达到给定值后,电流急剧下降,随后角速度出现超调,经过控制器的调节作用,最终角速度稳定到给定值,说明双闭环控制系统的动静态特性较好。图7为经过调整PI参数后、超调量达到σ%=10%的电机转矩和角速度曲线,其快速性较好,而且超调量也不大。

图6 转矩与角速度仿真波形

图7 转矩与角速度仿真波形
4 结束语
本文研究了永磁无刷直流电机的内环电流换,外环转速环的双闭环控制技术,推断了双闭环控制的数学模型,最后在Matlab/Simulink中进行仿真验证,仿真结果表明其采用双闭环控制技术的控制效果较为理想。
[1] 夏长亮.无刷直流电机控制系统[M].北京:科学出版社,2009.
[2] 王飞.永磁无刷直流电机控制系统的设计[M].北京:电子工业出版社,2009.
[3] 刘刚.永磁无刷直流电机控制技术与应用[M].北京:机械工业出版社,2010.
[4] 王峰,杨文焕,杨凯辰,等.无刷直流电机变频调速控制系统仿真研究[J].电子科技,2015,28(6):100-103.
[5] 方炜,张辉,刘晓东.无刷直流电机双闭环控制系统的设计[J].电源学报,2014,3 (2):36-42.
[6] 郑强,潘松峰,于西宗.基于Matlab 的无刷直流电机调速系统的建模与仿真[J].工业控制计算机,2012,25(9):39-42.
[7] 吕伟鹏.无刷直流电机双闭环串级控制系统仿真研究[J].电子设计工程,2011,19(24):30-34.
[8] 石俊,杨文焕,夏天宇,等.基于Cuk变换器的无刷直流电机转矩脉动抑制仿真[J].电子科技,2015,28(7):70-73.
[9] 夏鲲,杨益华,杨淑英,等.基于Z 源变换器的无刷直流电机转矩脉动抑制[J].系统仿真学报,2013,25 (11):2540-2545.
[10] 杨鹏,王飞,贾春奇,等.无刷直流电机闭环控制仿真系统的研究[J].微电机,2013,46(11):76-78.
[11] 徐晓冬,戴曙光.基于改进WFPSO算法的无刷直流电机模型分析[J].电子科技,2016,29(9):737-740.
[12] Zhang M H,Xia C L.Speed control of brushless DC motor based on single neural PID and wavelet neuron network[C].Harbin: IEEE International Conference on Control and Automation,2007.
[13] 钱双杰,简献忠,刘瑞.一种无位置传感器的无刷直流电机建模研究[J].电子科技,2015,28(6):195-199.
[14] 周阳,周美娇,殷弋.直流电机调速系统设计及PID参数整定[J].电子科技,2015,29(5):153-157.
[15] 洪乃刚.电力电子和电力拖动控制系统Matlab的仿真[M].北京:机械工业出版社,2006.
The Technology Research of Double Closed-loop Control System for Permanent Magnet BLDCM
YANG Zhenyu
(Engineering Department,China Geological Engineering Group Corporation,Beijing 100093,China)
For the shortcoming of big error for open-loop control and bad dynamic and static characteristics for single-closed loop control, the double-closed loop control system is studied for Permanent magnet. Firstly the paper introduces the working principle of PWM speed regulation for PMBLDCM, and then expounds the design process of the double closed-loop control system, and inferences the mathematical model of the current regulator and speed regulator in detail. Finally, the simulation results validate the double closed-loop control system of PMBLDCM has good dynamic and static characteristics.
brushless dc motor;PWM control;double closed loop control;modeling
2016- 11- 07
杨振宇(1975-),男,高级工程师。研究方向:自动控制。
10.16180/j.cnki.issn1007-7820.2017.04.042
TM36
A
1007-7820(2017)04-170-04
