基于细菌觅食与粒子群的改进混合算法
2017-04-21梁樱馨田浩杉
梁樱馨,田浩杉
(兰州交通大学 电子与信息工程学院,甘肃 兰州 730070)
基于细菌觅食与粒子群的改进混合算法
梁樱馨,田浩杉
(兰州交通大学 电子与信息工程学院,甘肃 兰州 730070)
针对粒子群优化算法(PSO)在优化过程中易陷入局部极值而产生“早熟”现象,文中提出一种基于细菌觅食与粒子群的改进混合算法。粒子群优化算法与细菌觅食优化算法的结合,增强了算法的全局搜索能力,使算法具有全局搜索能力强的优点。选用Matlab进行仿真实验,实验结果进一步显示了改进混合算法的优化能力优于基本PSO算法和基本BFO算法,收敛速度快,且具有较好的鲁棒性。
粒子群优化算法;细菌觅食优化算法;改进混合算法
群体智能(Swarm Intelligence, SI)的概念最早由Beni、Hackwood和Wang在分子自动机系统中提出,通过揭示和模拟自然现象而产生的一系列群体智能优化算法,该算法在模式识别、图像处理、工程等众多领域得到广泛的应用[1]。粒子群算法(Particle Swarm Optimization,PSO)是一种智能优化算法,最早由美国的Knnedy和Eberhart教授提出,其思想来源于人工生命和进化计算理论,是以模拟鸟群觅食行为为特征,以求解连续变量优化问题为背景的一种优化算法[2-3]。自PSO算法提出以来,由于它的计算快速性和算法本身的易实现性,引起了国际上相关领域众多学者的广泛关注和研究,经过短短几年时间的发展,已广泛应用于函数优化、人工神经网络训练、模糊系统控制等许多领域。然而,在应用过程中由于PSO算法种群多样性低,局部搜索能力差,搜索精度不够高,易陷入局部极值,造成收敛速度慢,计算复杂度高,最终解不精确的问题。
本文提出一种基于细菌觅食优化算法和PSO算法结合的混合算法。细菌觅食算法是基于大肠杆菌细菌觅食行为过程而提出的一种仿生随机搜索算法。该算法由于搜索时方向的随机变换,且细菌通过择优复制后以一定的概率迁徙到新的觅食区域中,增加了种群的多样性,降低了收敛于局部最优的概率,提高了找到最优解的概率,局部搜索能力强。仿真结果表明,改进混合算法的收敛速度比基本PSO算法快、优化效果更好,具有较好的鲁棒性。
1 粒子群优化算法
在粒子群优化算法中,可以将每个优化问题的潜在解看作是n维搜素空间上的一个点,称为“粒子”或“微粒”,并假定其是没有体重和重量的。所有的粒子均有一个被目标函数所决定的适应值,和一个决定其位置和飞行方向的速度,然后粒子们就以该速度追随当前的最优粒子在解空间中进行搜索,其中,粒子的飞行速度根据个体的飞行经验和群体的飞行经验进行动态调整。
假设Xi=(xi,1,xi,2,…,xi,n)是微粒i的当前位置,Vi=(vi,1,vi,2,…,vi,n)是微粒i的当前飞行速度,则粒子群优化算法的进化方程如下
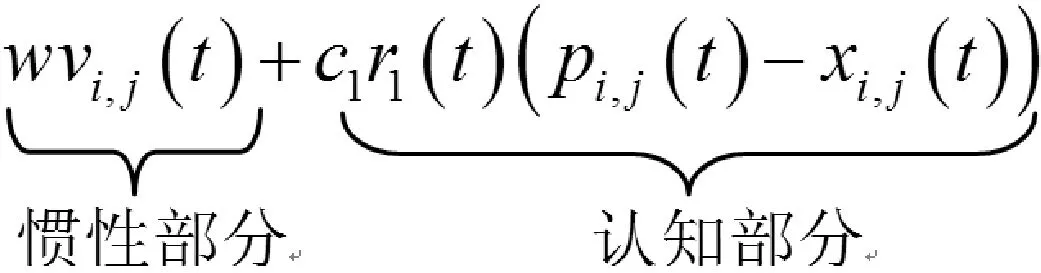

(1)
xi,j(t+1)=xi,j(t)+vi,j(t+1)
(2)
其中,w称为惯性权重系数;t表示迭代次数;pi,j(t)表示微粒i迄今为止经历的历史最好位置;pg,j(t)是当前粒子群搜索到的最好位置;c1、c2为学习因子,分别称为认知学习因子c1和社会学习因子c2,在0~2间取值。r1(t)和r2(t)是在[0,1]上的两个相互独立的随机数。
式(1)的第1部分为粒子的惯性部分,代表粒子的惯性行为;第2部分为粒子的“认知”部分,表示粒子个体对于自身的学习;第3部分为粒子的“社会”部分,表示粒子间的信息共享与相互合作。
2 改进细菌觅食算法
细菌觅食优化(Bacterial Foraging Optimization,BFO)算法是由K.M.Passion在2002年基于Ecolic大肠杆菌在人体肠道内吞噬食物觅食行为提出的一种新型仿生类优化算法[4]。细菌觅食优化算法是一种全局随机搜索算法,具有并行搜索等优点,该算法主要包括趋向、复制和迁徙3个步骤[5-7]。
2.1 趋向操作
趋向操作是细菌向食物源丰富区域聚集的一种行为,它包括细菌在觅食过程中的两个基本运动:旋转和游动。细菌先向某随机方向游动一步,若该方向上的适应值比上一步所处位置的适应值低,则进行旋转,朝另外一个随机方向游动;反之,则沿该随机方向向前移动[8]。
设细菌种群大小为S,细菌觅食算法中趋化行为具体描述如下
(3)
其中,θi(j,k,l)为细菌i在第j次趋向性操作、第k次复制操作和第l次迁徙操作后的位置;C(i)为细菌i的游动步长;Δ为随机方向上的一个单位向量。
由于在标准BFO算法中采用固定步长C(i),若将步长C(i)的值设置较大时,则细菌的收敛速度快,但易错过最优解或使算法陷入局部极小值而造成 “早熟”现象;反之,将步长C(i)的值设置较小时,虽然算法计算精度较高易找到最优解但降低了计算效率,算法收敛速度降低[9-11]。因此,每个细菌的步长大小均起着主要作用,本文通过改进细菌的游动步长C(i)在提高算法计算精度的同时保证算法的收敛速度,使得算法跳出局部极小值,如式(4)所示
C′(i)=C(i)×e-t
(4)
其中,t表示迭代次数。
BFO算法起始阶段,大部分细菌个体离全局最优点较远,为了增加算法的全局搜索能力,初始游动步长C′(i)的值较大;随着细菌迭代次数的增加,较多的细菌个体离全局最优越来越接近,且游动步长C′(i)的值也逐渐减小以便提高细菌个体的局部搜索能力,避免算法陷入局部极值而导致“早熟”现象的发生。
2.2 复制操作
一旦细菌生命周期结束,即到达临界趋化次数,细菌将进行繁殖。细菌的繁殖过程遵循自然界“优胜略汰,适者生存”原则。以趋化过程中各细菌适应值累加和为标准,较差的细菌死亡,较好的细菌分裂成两个子细菌。子细菌将继承母细菌生物特性,具有与母细菌相同的位置及步长[11-12]。
2.3 迁徙操作
实际环境中的细菌所生活的局部区域可能会发生逐渐变化,这样可能会导致生活在这个局部区域的细菌种群被迁徙到新的区域中去,在BFO算法中模拟这种现象称为迁徙性操作。
BFO算法中菌群经过若干代复制后,细菌以给定概率执行迁徙操作,被随机重新分配到寻优区间。迁徙操作使得细菌可能更靠近全局最优解,从而有利于跳出局部最优解,进而寻找全局最优解[13-16]。
3 改进细菌觅食与粒子群混合算法
粒子群算法与细菌觅食算法在优化问题中均具有较好的优化性能,也均存在各自的缺点。虽PSO算法参数设置少,全局搜索能力强,但在实际应用过程中算法缺乏粒子多样性,在算法后期容易陷入局部最优值;BFO算法中的趋向操作具有变换方向的搜索特性,可根据适应值的变化决定是否继续沿该方向继续搜索,提高了局部搜索能力,具有较高的搜索精度,但是BFO算法全局搜索能力不强,没有对菌群最优信息的记忆能力。本文将两种算法相互结合并加以改进,取长补短,提高了算法的性能和效率,如式(5)所示。
式(7)中,去除了式(1)PSO算法速度更新公式中的个体认识部分,利用PSO算法对于群体信息共享的记忆功添加到改进的BFO算法位置更新方程中,更好的提高BFO算法的全局搜索能力和搜索效率。
算法主要实现步骤如下:
步骤1 初始化参数S,Ned,Nre,Nc,Ns,Ped,ω,c1,c2,r1,r2其中,S为细菌种群大小;Ned为最大迁徙代数;Nre为最大复制代数;Nc为最大趋向代数;Ns为游动的最大步长;Ped为迁徙概率;w为PSO算法中的惯性权重系数;c1和c2为PSO算法中0~2之间学习因子,r1和r2是PSO算法中[0,1]上两个相互独立的随机数;
步骤2 随机初始化菌群位置,并计算每个细菌的初始化适应度函数值J;
步骤3 迁徙循环l=l+1;
步骤4 复制循环k=k+1;
步骤5 趋化循环j=j+1。
(1)计算细菌适应度函数J(i,j,k,l),记细菌i目前最优适应值。Jlast=J(i,j,k,l);
(2)旋转:产生一个随机向量Δ(i)∈Rn,其中每一个元素Δx(i),(x=1,2,3,…,n)是分布在[-1,1]上的随机数;
(3)游动:当m
步骤6 若j 步骤8 若k 步骤9 每个细菌按照迁徙概率Ped被随机分布到寻优空间中。若l 图1 改进混合算法流程图 4.1 测试函数 为了验证改进细菌觅食和粒子群混合算法的性能,选用仿真工具Matlab对其进行仿真模拟[17],并将其与标准BFO、标准PSO算法进行比较。本文选取的测试函数如表1所示。 表1 测试函数 如表1所示,上述4个函数均是典型的测试函数,均可取到全局极小值0。基本细菌觅食算法可以优化低维单峰函数,且得到较好的结果,但对于高维且多峰的函数问题,优化结果并不理想。为了验证改进后的混合算法对高维多峰函数的优化性能,将4个函数的维度均设置为30。 4.2 参数设置 设在上述算法中细菌种群大小S=100,最大迁徙代数Ned=2,最大复制代数Nre=4,最大趋向代数Nc=10,游动的最大步长Ns=4,迁徙概率Ped=0.25,惯性权重系数w=0.75,社会学习因子c2=2 。 4.3 实验结果 为了测试改进混合算法的性能,本文用改进混合算法分别对上述四个函数独立运行30次寻优,并与标准的BFO和标准的PFO算法的测试结果进行比较。实验结果如表2所示,改进混合算法在函数f1、f2、f3、f4中运行其求解精度明显优于基本的BFO和PFO算法,表现出良好的性能。 此外,以 函数为例,对算法的收敛速度加以比较,比较结果如图2所示,改进混合算法可增加算法的收敛速度,使算法在较少的迭代次数内就准确的收敛到全局最优点,其表现优于基本BFO和基本PSO算法。 表2 实验结果 图2 基于f3的3种算法收敛曲线图 本文在基本细菌觅食算法和粒子群算法的基础上,将两种算法相互结合并加以改进。结果表明,改进的混合算法在收敛速度、计算精度及鲁棒性方面均优于基本算法,更能有效的避免算法陷入局部最优值,同时表现出较好的全局搜索能力,适用于求解复杂优化问题。 [1] 王枚,朱云龙,何小贤.群体智能研究综述[J].计算机工程,2005,31(22):194-196. [2] Kennedy J,Eberhart R C.Particle swarm optimization[C].UT,USA:Proceedings of IEEE International Conference on Neural Networks,1995. [3] Eberhart R C,Kenndy J.A new optimizer using particle swarm theory[C].Japan: Proceeding of the 6th International Symposium on Micro Machine and Human Science,1995. [4] Passino K M.Biomimicry of bacterial foraging for distributed optimization and control[J].IEEE Control Systems Magazine,2002,22(3):52-67. [5] Sasithradevi A, Singh N N. Synergy of adaptive bacterial foraging algorithm and Particle Swarm Optimization algorithm for image segmentation[C].MA,USA:International Conference on Circuit, Power and Computing Technologies (ICCPCT), IEEE, 2015. [6] 章国勇,伍永刚,谭宇翔.一种具有量子行为的细菌觅食优化算法[J].电子信息学报,2013,35(3):614-621. [7] 肖文显,褚镭郦,王俊阁,等.自适应细菌觅食算法在优化问题中的应用[J].安徽大学学报:自然科学版,2015(4):31-36. [8] 姜建国,周佳薇,郑迎春,等.一种自适应细菌觅食优化算法[J].西安电子科技大学学报:自然科学版,2015,42(1):75-81. [9] 胡爱策,任明仑,王浩.粒子群与细菌觅食相结合的案例聚类算法[J].计算机技术与发展,2013,23(10):44-47. [10] 张学良,刘丽琴.智能优化算法及其在机械工程中的应用[M].北京:国防工业出版社,2012. [11] Dasgupta S, Das S, Abraham A, et al. Adaptive computational chemotaxis in bacterial foraging optimization: an analysis[J]. IEEE Transactions on Evolutionary Computation, 2009, 13(4):919-941. [12] Raj J S,Vasudevan V.Smart bacterial foraging optimization algorithm for scheduling in grid[J].European Journal of Scientific Research,2013,94(2):253-260. [13] 周雅兰.细菌觅食优化算法的研究与应用[J].计算机工程与应用,2010,46(20):16-21. [14] 王雪松,程玉虎,郝名林.基于细菌觅食行为的分布估计算法在预测控制中的应用[J].电子学报,2010,38(2):333-339. [15] Kim D H,Abraham A,Cho J H.A hybrid genetic algorithm and bacterial foraging approach for gobal optimization[J].Information Sciences,2007,177(18):3918-3937. [16] Kn L, Reddy B R, Kalavathi M S. Adaptive bacterial foraging oriented particle swarm optimization algorithm for solving optimal reactive power dispatch problem[J]. Chronexus Org, 2014,3(1):1-6. [17] 刘卫国. Matlab程序设计与应用[M].2版.北京:高等教育出版社,2006. Improved Hybrid Algorithm Based on Bacterial Foraging and Particle Swarm Optimization LIANG Yingxin,TIAN Haoshan (School of Electronic and Information Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China) Aiming at the phenomenon that the particle swarm optimization algorithm is easy to fall into the local extremum in the optimization process, an improved hybrid algorithm based on bacterial foraging and particle swarm optimization is proposed. Particle swarm optimization algorithm and the bacterial foraging optimization algorithm combined, the enhanced algorithm Alto global searching ability. The algorithm has the advantages of strong global search ability. Matlab simulation experiment, the results show that the improved hybrid algorithm is better than the basic PSO algorithm and the basic BFO algorithm, the convergence rate is fast, and has good robustness. particle swarm optimization; bacterial foraging algorithm; hybrid algorithm 2016- 05- 10 梁樱馨(1992-),女,硕士研究生。研究方向:无线通信等。田浩杉(1992-),男,硕士研究生。研究方向:无线通信。 10.16180/j.cnki.issn1007-7820.2017.04.020 TP301.6 A 1007-7820(2017)04-079-04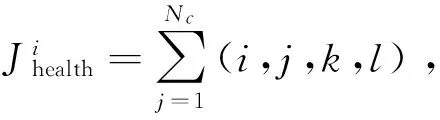
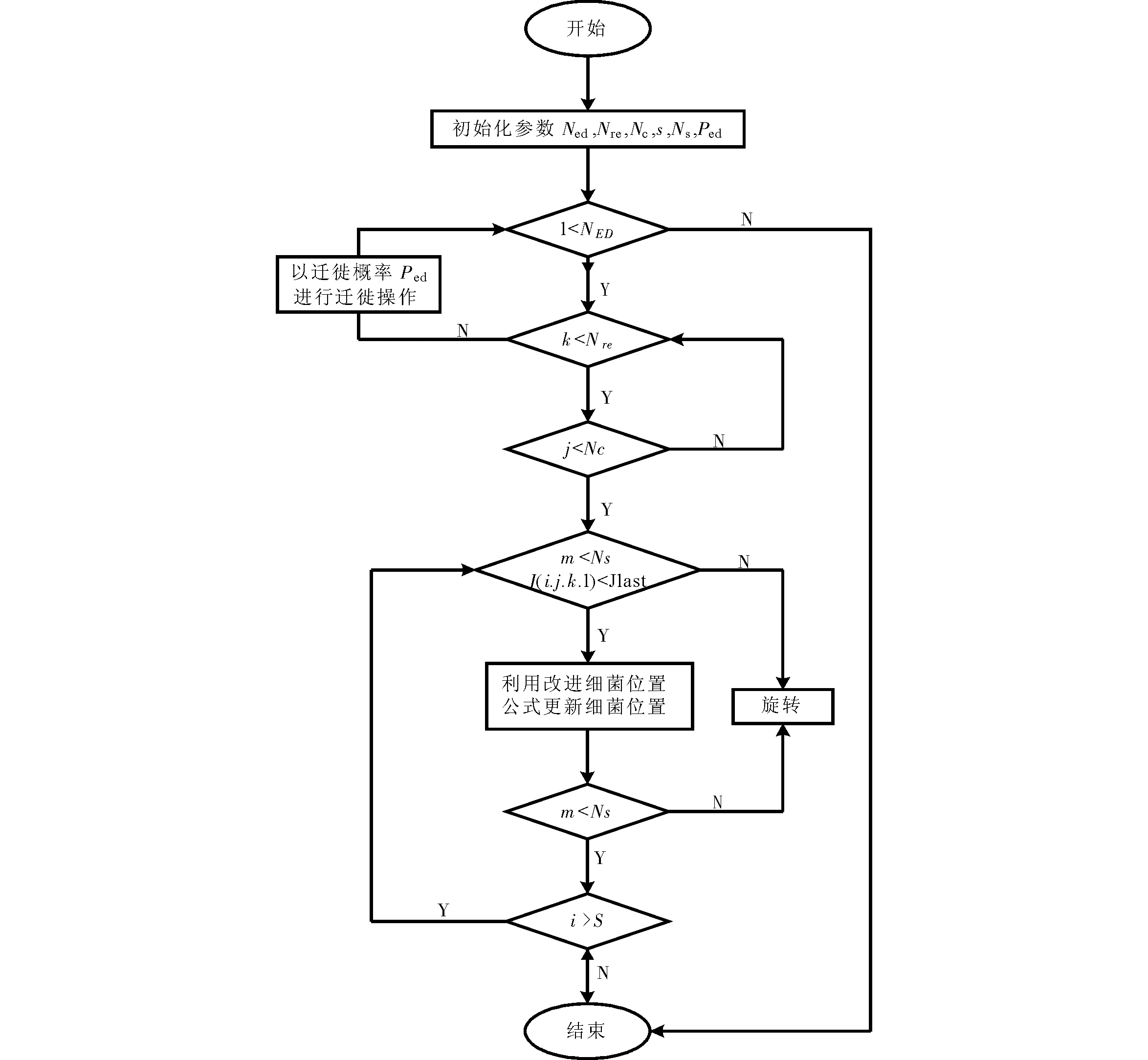
4 仿真实验与分析

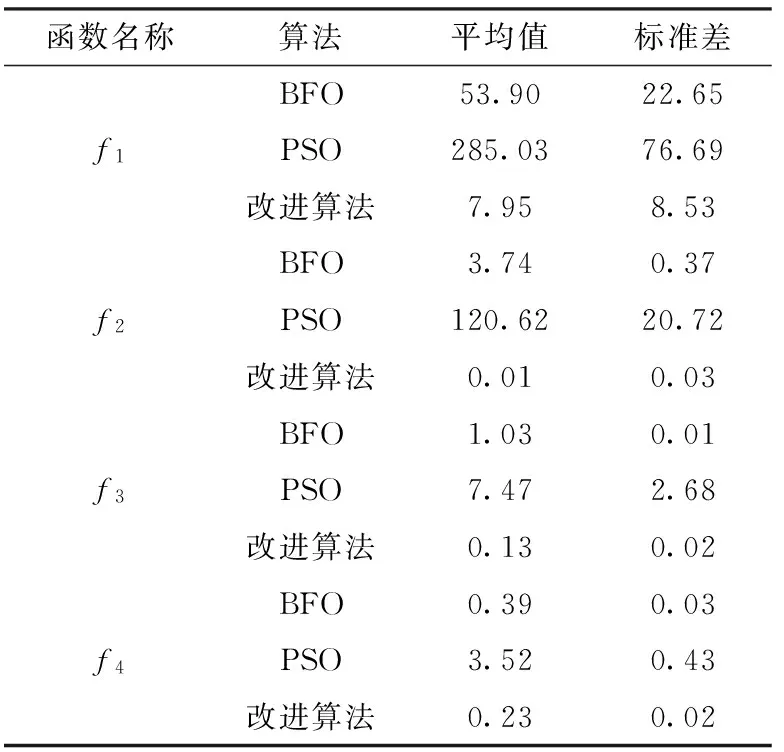
5 结束语
