基于改进蚁群算法的公交疏散策略研究

赵惠光，何胜学，黄 清，向乐佳

(1.上海理工大学 管理学院，上海 200093；2.周口师范学院 新闻与传媒学院，河南 周口 466001；3.上海同技联合建设发展有限公司，上海 200092)

基于改进蚁群算法的公交疏散策略研究

赵惠光1，何胜学1，黄 清2，向乐佳3

(1.上海理工大学 管理学院，上海 200093；2.周口师范学院 新闻与传媒学院，河南 周口 466001；3.上海同技联合建设发展有限公司，上海 200092)

针对无预警灾难发生后的大规模人群疏散问题，提出了应急救援的公交疏散策略，通过对动态的疏散路网和疏散者的时间加载离散化处理，采用时空网络和数值分析的方法以疏散总时间最短，伤亡人数最少建立公交疏散的非线性混合整数规划模型，并将整个公交疏散过程与改进的蚁群算法相结合，通过信息素全局更新对疏散模型进行求解，最后以一个简单的公交疏散网络作为算例来求解最优疏散路径。结果表明，通过多次计算不仅验证了改进蚁群算法的有效性，同时求解疏散路径的速度和质量也得到提高。

非线性混合整数规划；公交疏散；蚁群算法；应急救援

无征兆自然灾害、突发社会生产事故以及恐怖主义袭击往往会造成严重的人员伤亡，财产损失，如印度洋海啸和8·12天津滨海新区爆炸事故等，对于社会安全和应急疏散体系构成较大的威胁，使得各国开始重视紧急疏散策略的研究[1]。目前我国的灾后疏散一般由应急疏散部门调集大运量的公交在短时间内疏散事故区域内人群至安全避难区域，是一种较为可行的灾后疏散交通组织形式。

紧急公交疏散路径的优化问题属于组合优化问题，是NP-hard问题，其中Bish[2]以最小化最大行车成本为目标，构建了基于弧段的混合整数规划模型。Yamada[3]运用最小成本流问题进行疏散交通分配，提出了最短路撤退规划方法。Tuydes 和Ziliaskopoulos[4]提出了一个基于混合线性整数规划的分阶段疏散模型。何胜学[5]提出了将时间滚动式的流量加载模式与经典遗传算法相结合来确定公交疏散中车辆的最佳路径问题。

本文将从以时空网络的形式引入路网的交通动态特征，同时考虑疏散者的时间流量加载性，对应急救援公交疏散策略进行检验。

1 基本描述

1.1 路网转化

时空网络是离散时间下的动态网络流建模方法[6]，它通过将节点和弧构成的静态的网络按一定的时间间隔在离散时间框架下进行相应的节点“复制”和弧段更新，从而形成“新”的网络，然后按照静态网络流问题的建模方法在“新”网络上进行建模，对“动态”路径规划问题的分析[7]。为体现动态的交通网络特征，假设弧段上的运行时间在疏散过程中保持不变，这里将现实中的交通路网转变成时空网络来研究，如图1所示。

图1 静态的时空网络

(1)图中所示的时空网络。G=(A,H),A=AD∪AC∪AS∪AE，其中，A是时空网络中所有节点的集合;AD为车站节点集合;AC为所有上车点集合(包括公交站点和车站节点);AS为避难点集合;AE为一个虚拟终点节点(代表所有公交车和待疏散者最终的目的地)；

(2)H表示时空网络中所有弧段的集合：H=HW∪HC∪HE∪HS，图1中HW为等待弧子集，即相邻两个时段，同一上车点时空网络节点之间的连接弧，其时间间隔Δt,用短虚线来表示； 为移动弧子集，弧上的最大通行能力为弧上总的公交车辆容量，相应的运行时间为Δt=tj-ti，用实线来表示；HE为终点连接弧子集，是避难点节点与终点节点之间的连接弧，代表成功疏散弧段，将其行程时间设置为ti,AE=0，最大通行能力为无限大。HS是上车点节点与终点节点之间的连接弧，最大通行能力也为无限大，为最大程度的减少伤亡人数，给其疏散时间一个给定的很大的惩罚因子Z，ti,AE=Z，以此来代表伤亡人数用长虚线表示。

1.2 基本参变量

考虑无预警紧急疏散的时间紧迫性，一般假设每一辆公交车辆在有效救援时间内只进行一次从车站到避难点的疏散[8]。

路段：对任一路段(i,j)，这里i和j分别是弧段头尾节点，定义tij，xij，yij分别表示该路段上的行程时间，待疏散者流量和参与救援的公交车数量。

节点：节点AD、AC和AS具有位置pi和时间ti两个属性[9]，位置属性根据原疏散网络中的相应位置而生成，一共包含T+1层，每一层代表一个时间段，时间段ti∈{0,1,2,…,T}；时间间隔Δt的选取需要满足所有弧段的运行时间是选取的最短时间间隔时长的整数倍，即t有效=TΔt；AE时间属性定义为tAE=T+1。

对于xij，yij分别定义二值指示变量μij,ηij来表征弧段上疏散者的流量状态[10]，μij,ηij∈{0,1};μij和ηij的具体值可参考式(1)和式(2)。

(1)

(2)

V表示所有可获得的用于疏散的公交车所构成的集合，因此有|V|=V。Vi和Vij分别表示穿过点i和弧段(i,j)的公交车辆所构成的集合，于是有yij=|Vij|。

2 应急公交疏散策略

2.1 基本约束条件

这里考虑公交车辆的不同载客量、有容量限制的避难点、疏散者和救援公交车辆的流量守恒等因素，将相关约束条件详细介绍如下。

在路段节点处待疏散者流量守恒[11]，相关约束如下

(3)

在路段节点处公交车辆流量守恒，相关约束如下

(4)

(5)

(6)

对公交车辆载客量进行约束，即弧段上的疏散者人数不能超过弧段上公交车的总装载容量，相关约束如下

(7)

对避难点的容纳容量进行约束，即到达所有避难点的待疏散者总人数不能超过该避难点的最大容纳能力，相关约束如下

xASAE≤CS

(8)

(9)

对任意等待弧(i,j)，如果与该弧相关联的上车点上有待疏散者等待却没有公交车，那么离开该上车点的公交车一定没有剩余容量，相应约束如下

(10)

除等待弧之外的其他弧上待疏散者人数与当前公交车的加载量之间的关系可用下式来表示

(11)

待疏散者登上公交车后不允许中途变更车辆，相关约束如下

Qv(t)≤Qv(t+1),∀v∈Vt∈{1,2,3,…,T}

(12)

待疏散者流量和公交车流量为非负整数，相关约束如下

xij,yij∈Z+∪{0},(i,j)∈H

(13)

以上式(1)～式(13)即为建立无预警式公交疏散路径模型的相关约束条件。

2.2 考虑加权的公交疏散路径规划模型

目标函数分为5 部分，利用参数ηij将等待弧进行区分计算，则待疏散者在公交车外的等待时间

TWO=∑(i,j)∈HW(1-ηij)xijtij

(14)

待疏散者在公交车内的等待时间

TWI=∑(i,j)∈HWηijxijtij

(15)

待疏散者在公交车上的运行时间

TR=∑(i,j)∈HCxijtij

(16)

未成功疏散的待疏散者的惩罚时间

TZ=∑(i,j)∈HSxijtij

(17)

公交车的总运行时间

TV=∑(i,j)∈Hyijtij

(18)

同样给每一部分分别设定一个非负权重，分别为αWO、αWI、αR、αZ和αV，那么目标函数为

F(x,y)=αWOTWO+αWITWI+αRTR+αZTZ+αVTV

(19)

最后由约束条件式(1)～式(18)构成的约束集H(x,y)和目标函数式(19)，建立应急公交疏散策略规划模型为

(20)

3 算法设计

针对应急公交疏散路径规划问题，本文将改进的蚁群算法[12]融合到应急公交疏散策略中去，求解步骤如下：

步骤1 初始化参数。假设有效的疏散时间t有效和时间间隔Δt，则ti∈T={0,1,2,…,t有效/Δt}；未成功疏散者的疏散惩罚时间Z；最大迭代次数为ε；弧段上的初始信息素强度为τij；各弧段的长度以及用于疏散的公交车集合V；改进蚁群算法的信息素更新[13]的改进公式为

(21)

转移概率[14]为

(22)

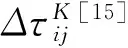
(23)

ZK=第K只蚂蚁完成一次寻优任务后，其所走过的路径长度；Q为一个常数。设迭代次数K=1；

步骤2 路网转化。将给定的原始的公交疏散路网转化成相应的时空网络G=(A,H)；

步骤3 公交疏散路径的优化步骤。对所有蚂蚁即所提供的公交车集合V中的所有公交车进行如下操作：

(1)当t(K)=0时，将所有蚂蚁放置在时空路网中节点(1, 0)的初始车站节点，此时每只蚂蚁的剩余装载容量Remain为最大载客量；

令t(K)=t(K)+1,i=j;

(3)若蚂蚁的时间属性t(K)≥T或蚂蚁的位置属性p(K)=AS时，则将蚂蚁强制移动到最终的终点AE处，则蚂蚁找到一条弧段。待所有蚂蚁全部到达终点后，转到步骤4；否则，转到步骤(2)；

步骤4 信息素全局更新[16]。待所有蚂蚁全部到达终点后，计算每只蚂蚁生成的弧段长度Zk，并计算出总疏散时间，保存目前为止所找到的最优弧段。根据公式更新信息素的轨迹强度τij； 令k=k+1，并重置Δτij=0，转到步骤5；

步骤5 迭代终止。如果当前迭代次数τ=ε，计算终止；否则，转到步骤3；

步骤6 输出所有蚂蚁最优疏散弧段及疏散总时间。

4 算例分析

针对应急公交疏散的实际情况，以一个简单的公交疏散网络来计算最优疏散路径，并验证改进蚁群算法的有效性。

图2是一个公交疏散路网图，节点1 代表车站节点；节点2、3 和4 代表上车点节点；节点5 代表避难所节点。

图2 公交疏散网络图

需要利用公交车进行疏散的待疏散者到达公交站站点的到达情况如表1所示。

表1 疏散者到达公交站点的情况

假设有效的疏散时间t有效=4，时间间隔Δt=1，那么相应的时间段为ti∈T={0,1,2,3,4}，时空网络分为5层，终点节点对应的时间段为5，规定待疏散者和公交车最终全部到达终点节点。

设定未成功疏散惩罚时间为Z=1，蚁群算法中最大迭代次数为ε=10，各个路段上的初始信息素强度为τij=0，初始信息素强度增量为Δτij=0，给出常数Q的值、信息素强度的相对重要性α=1及能见度的相对重要性β=1，信息素挥发因子ρ=0.5，各路段的长度均为1， 3辆公交车V1、V2和V3从车站1出发，最大载客量为90，设定非负权重αWO=1、αWI=1、αR=1、αZ=1和αV=1。

经过计算分析，相关结果如下，相应疏散路线及流量如表2～表4 所示。

表2 公交疏散时间及相关路段的流量

表3 公交疏散时间及相关路段的流量

表4 公交疏散时间及相关路段的流量

当常数Q取3时，算例能够得到一个比较满意的结果，不仅提高模型的求解速度，解得质量也得到提高。

5 结束语

针对应急救援中的公交疏散策略进行了研究，通过模拟实际的应急疏散过程，利用改进的蚁群算法求解公交疏散模型，给出了模型的一个有效求解算法，可以看出改进的蚁群算法提高了求解模型的速度，为应急公交疏散提供了一个具体可行的优化方案。

[1] 刘小明,胡红.应急交通疏散研究现状与展望[J].交通运输工程学报,2008(3):108-115,121.

[2] Yamada T.A network of approach to a city emergency evacuation planning[J].International Journal of Systems Science,1996,27(10):931-936.

[3] Tuydes H,Ziliaskopoulos A.The network evacuation problem and solution algorithms[C]. San Francisco:Informs Annual Meeting,2005.

[4] Bish D.Planning for a Bus-based Evacuation[J]. ORSpectrum,2011,33(3):629-654.

[5] 何胜学.无预警紧急疏散中公交车辆路径的确定方法[J].运筹学学报,2014(3):47-59.

[6] 崔建勋,安实,崔娜.基于时间扩展网络的区域疏散公交路径规划[J].华南理工大学学报:自然科学版,2010(3):64-69.

[7] 庞明宝,东方,任沙沙.基于时间依赖网络的城市交通紧急疏散线路研究[J].公路交通科技,2011(1):100-106.

[8] 刘云忠,宣慧玉.车辆路径问题的模型及算法研究综述[J].管理工程学报,2005(1):124-130.

[9] 徐梁,宋瑞.自然灾害下的公交疏散路线模型[J]. 物流技术,2011(11):147-150,154.

[10] 黄隆飞,宋瑞,郑锂.大容量客车疏散路径模型选择[J].交通信息与安全,2009(5):85-89.

[11] 宋瑞,何世伟,章力.紧急疏散情况下的公交车运行计划优化研究[J].交通运输系统工程与信息,2009(6):154-160.

[12] 倪庆剑,邢汉承,张志政,等.蚁群算法及其应用研究进展[J].计算机应用与软件,2008(8):12-16.

[13] 陈迎欣.基于改进蚁群算法的车辆路径优化问题研究[J].计算机应用研究,2012,29(6):151-156.

[14] 段海滨,王道波,朱家强,等.蚁群算法理论及应用研究的进展[J].控制与决策,2004(12):1321-1326,1340.

[15] 高尚,杨静宇.非线性整数规划的蚁群算法[J]. 南京理工大学学报:自然科学版,2005(S1):126-129.

[16] 苏红畏,刘希玉,王晓敏.混合最大最小蚁群算法在VRPTW中的应用[J].计算机技术与发展,2010(2):90-94.

Study on the Strategy of Bus Evacuation Based on Improved ant Colony Optimization

ZHAO Huiguang1，HE Shengxue1，HUANG Qing2，XIANG Lejia3

(1.Business School,University of Shanghai for Science and Technology,Shanghai 200093,China;2. College of Journalism and Communications,Zhoukou Normal University,Zhoukou 466001,China;3. Shanghai Tongji United Construction Development Co.,Ltd , Shanghai 200092,China)

Aim at the evacuation problems of large-scale crowd after the disaster without warning, presents the strategy of bus evacuation during the emergency rescue, puts forward the dynamic evacuation network and time load processing discretization, adopt the methods of numerical analysis and time-space network to shortest the total evacuation time ,minimum the casualties, then establish the mixed integer nonlinear programming model of bus evacuation, combined the evacuation process with improved ant colony optimization, proposed global pheromone updating to resolving the evacuation model, finally,to achieve the optimal evacuation path in an ordinary bus evacuation network.the results verified the validity of the algorithm by many times calculation ,and improved the speed and quality of solving the evacuation path.

bus evacuation;mixed integer nonlinear programming;ant colony optimization;emergency rescue

2016- 05- 26

国家自然科学基金资助项目(70672110);上海市(第三期)重点学科基金资助项目(S30504);上海市教委科技创新基金资助项目(10YS105);上海理工大学博士启动基金资助项目(1D-00-307005)

赵惠光(1991-),男,硕士研究生。研究方向:系统工程等。 何胜学(1976-)，男，博士，副教授，硕士生导师。研究方向：系统工程等。

10.16180/j.cnki.issn1007-7820.2017.04.017

U491，TP301

A

1007-7820(2017)04-068-05