基于重复和PR复合控制的单相PWM整流器的研究

刘鹏飞, 王君艳

(上海交通大学 电气工程系，上海 200240)

基于重复和PR复合控制的单相PWM整流器的研究

刘鹏飞, 王君艳

(上海交通大学 电气工程系，上海 200240)

如何减少交流侧电流谐波对电网的影响，是PWM整流器控制的关键问题。针对谐波产生的主要原因，提出了基于重复和PR的复合控制策略。PR控制实现了对正弦电流的无静差跟踪，重复控制利用其 内模实现了对谐波扰动的记忆和修正。并基于MATLAB对单相PWM整流器进行了仿真，对比了PR控制、重复控制和基于重复和PR复合控制三种方案的仿真和实验结果，复合控制策略使得交流侧电流谐波少、动态响应快，对电网谐波扰动有更好的抑制效果。

PWM整流器；比例谐振控制；重复控制；复合控制；电流谐波

0 引 言

单相PWM整流器因可使其电网侧电流正弦化，并运行在单位功率因数等优点，被广泛应用于不间断电源和电力机车传动系统中[1]。由于电网扰动、开关死区以及数字信号延时等影响，导致单相PWM整流器交流侧电流谐波畸变率增大，从而对电网产生了严重谐波污染。而传统的PI控制对交流侧电流控制不够理想[2,3]。

针对于此，提出了基于重复和PR的复合控制策略。PR控制能实现对正弦参考电流的无静差跟踪[4-6]。重复控制用于改善系统的稳态性能，抑制电网等对交流侧电流的周期性扰动。将两种控制方法相结合，从而提高交流侧电流的控制品质。

1 单相PWM整流器的数学建模

单相PWM整流器主电路如图1所示，由4个IGBT和续流二极管反并联构成的电压型桥式电路。T1-T4为IGBT，VD1～VD4为续流二极管，Ls为电网一侧的滤波电感，Cdc为直流侧滤波电容，Rdc为负载电阻。

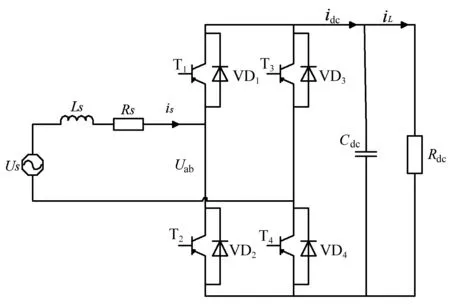
图1 单相PWM整流器主电路

对图1，有如下方程：

(1)

由式(1)可得：

(2)

图1的直流侧有如下方程：

(3)

根据式(1)-(3)绘出的控制系统结构框图如图2所示，α为电压环反馈系数，β为电流环反馈系数，KPWM为PWM电路的等效增益。IGBT触发脉冲与PWM整流器输出电压之间的滞后环节(延时最多不超过一个开关周期，在0-Ts之间，取为统计平均值0.5Ts，可用一阶惯性环节近似此滞后环节)。S为开关函数，对于双极性SPWM调制，在一个载波周期内(等于Ts)：

为了实现零稳态误差以及网测电流正弦化，控制系统采用电流内环和电压外环的双环控制策略。外环是直流侧电压控制环，其功能是保持直流侧电压稳定。内环为电流环，其功能是保证输入电流呈正弦并且与电网电压同步[7]。

图2 控制系统结构框图

2 重复控制在PWM整流器电流环控制中的应用

图3 重复控制框图

重复控制是基于内模原理的一种控制方法。即在一个闭环调节系统中，在其反馈回路中设置一个内部模型，使该内部模型能够很好地描述系统外部信号特性，即是上一个基波周期中出现的波形畸变会在下一个基波周期的同一时间重复出现，控制器便可以根据给定信号和误差信号确定所需要校正的信号[8]，达到抑制谐波的目的。其控制框图如图3所示。

其中q取略小于1的常数或一阶低通滤波器，以牺牲系统一定的跟踪精度来保证稳态裕度，选取q=0.95。C(z)为补偿器，G(z)为被控制对象，d为等效周期性干扰。

由图1控制系统结构框图的电流内环可以得到被控对象的传递函数：

(4)

其中KPWM=212，β=1/12，Ls=3 mH，Rs=0.2 Ω。

设控制器的控制开关为10 kHz，经过零阶保持器法Z变换后得到：

(5)

图4 G(z)的Bode图

图5 C1(z)G(z)的Bode图

其Bode图见图4，由图可知，中低频段控制对象增益为40 dB，并且在中低频段有一定的相位滞后。

采用重复控制需要对控制对象的幅频特性和相频特性进行校正和补偿，其目的是使被控制对象在中低频段增益为0 dB，零相位。在高频段，增益快速降低。补偿函数C(z)具有如下形式：

C(z)=KrZkC1(z)C2(z)

(6)

其中C1(z)为滤波器，作用为抵消被控制对象G(z)靠近单位圆的极点，并且校正增益到0 dB。由式(5)可得，系统的极点z1=0.997 3,z2=0.367 7。选取z1靠近单位圆的极点，则取：

(7)

经过C1(z)补偿后的Bode图如图5所示，由图可知，控制对象在中低频段已经被补偿至0 dB，但是高频段依然下降较为缓慢。因此引入二阶低通滤波环节C2(z)。其作用是增强高频衰减，从而提高系统的稳定性。由图5可得，截止频率为6 000 rad/s。为了防止振荡现象出现，选取阻尼比1.2>0.707。这样可以得到:

(8)

经过零阶保持器法Z变换后得到：

(9)

Zk为超前环节，用来补偿被控制对象G(z)和补偿器C1(z)C2(z)所引起的总相位滞后。取k=9，即补偿器为Z9。

Kr为重复控制的增益系数，其值与稳态误差成反比，与系统的稳态裕度成正比。通常选取Kr=0.95，可以得到比较理想的调整效果。

图6 C(z)G(z)的Bode图

图6为C(z)G(z)的Bode图。由图可知，C(z)G(z)的增益在低频段至0 dB，并且为零相位，系统稳定精度高。在高频段增益快速降低，对高频信号有良好的抑制作用。

3 PR控制在PWM整流器电流环控制中的应用

PR控制环节由比

例环节和谐振环节组成，可以对正弦量进行无静差调节，同时对系统进行快速响应，使系统具有更好的动态特性。

在实际系统中实际应用中，多采用准PR控制器，其传递函数为：

(10)

式中ω0为给定信号谐振角频率。取定系统频率为50 Hz，则ω0=100π。谐振因子KR与PR调节器在谐振频处的增益相关，KR减少的时候，控制器的全频率范围增益会随之减少，但是系统带宽保持不变。截止频率影响谐振带宽，ωc越小，PR调节器对输入信号的调节效果越明显。比例因子Kp决定了控制器的幅值裕度、相角裕度以及动态性能。图7为改进型PR控制器在Kp分别为100，10，1，0.1时的Bode图。从图7中随着Kp增大，谐振带宽以外的幅值也会随之增大。

图7 改进型PR调节器随Kp变化时Bode图

合理配置ωc，KR，Kp的值可以使系统在谐振处的增益降低，增加其带宽，并且降低系统对频率波动的敏感性，在保证稳态性能的同时增强了抗干扰能力。准PR控制器参数：ωc=2π，KR=100，Kp=4。

将前面分别设计的重复控制器和PR控制器并联构成复合控制器来对电流内环进行控制，见图1。

4 仿真与实验分析

4.1 仿真结果

为了验证所提出控制策略的正确性,采用的MATLAB/Simulink进行建模和仿真。主电路参数如表1所示。

图8～10分别为采用PR控制、重复控制以及复合控制三种方法的交流侧电流波形图，图11～13分别为对应的谐波分析图。从图上可以看出，稳态时三种方法都能很好实现交流侧电流与电网电压同频同相。图8中PR控制能够很好实现无静差跟踪，并且对于电流跟踪有很好的动态响应，但是电流谐波畸变严重，波形的THD达到了4.14%。图9中重复控制虽然对电流畸变有一定的抑制性，但是动态响应较慢，THD为3.45%。图10中复合控制集合了两者的优点，在快速响应的同时也保证了输出波形的质量，THD为2.31%。从图14可知，复合控制下直流侧电压稳定，实际输出电压为351.2 V,纹波电压±4 V左右，纹波电压为输出电压的±1.14%左右，达到了设计的要求。

表1 仿真实验参数

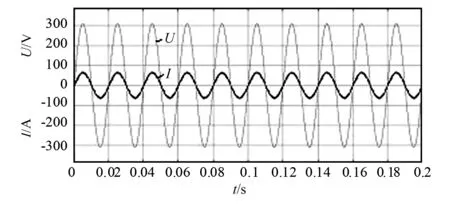
图8 PR控制仿真图

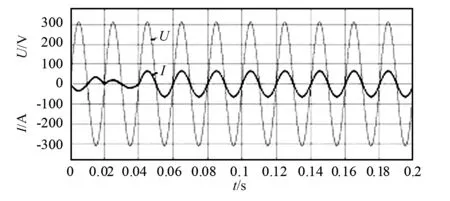
图9 重复控制仿真图

图10 复合控制仿真图

图11 PR控制谐波分析

图12 重复控制谐波分析图

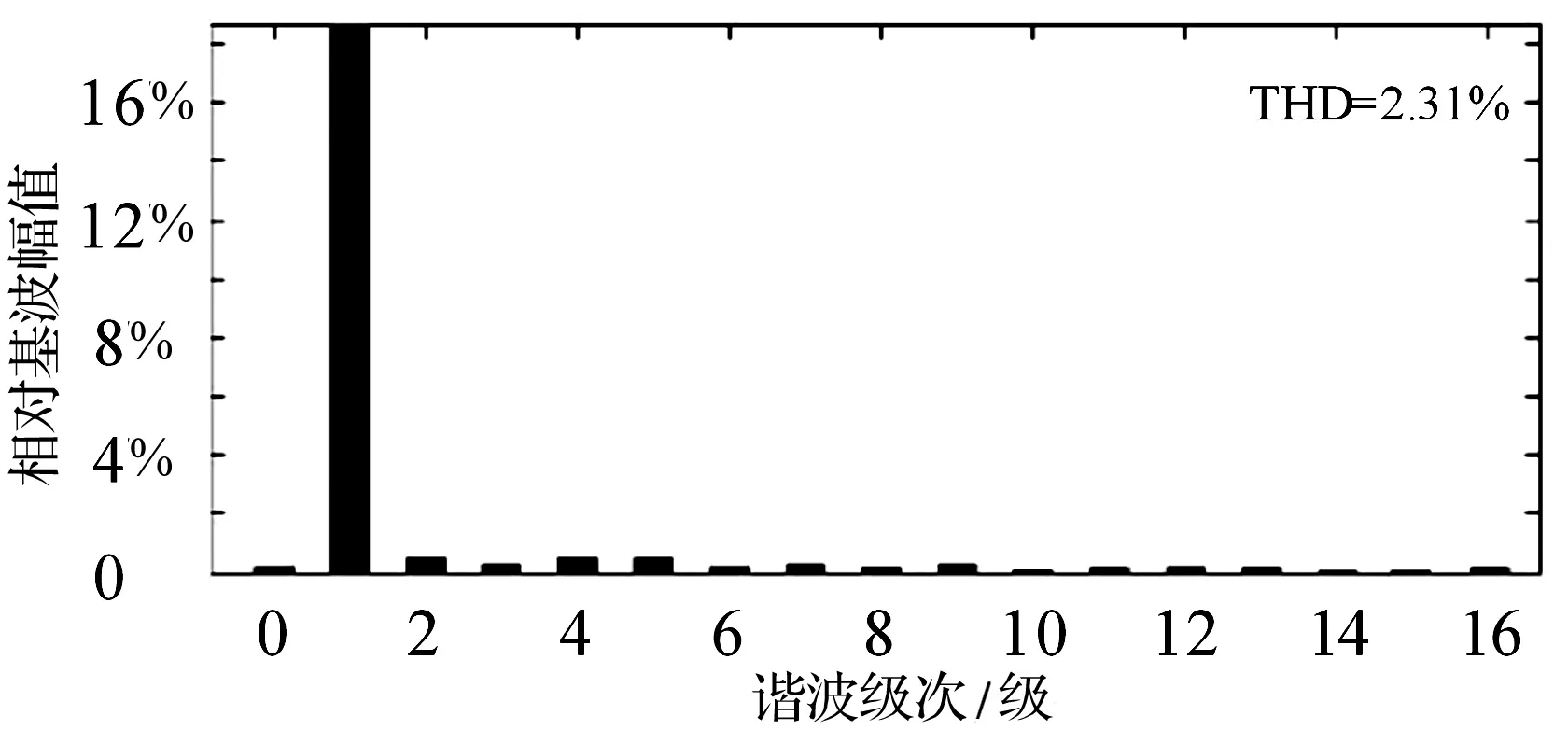
图13 复合控制谐波分析图

图14 复合控制下直流侧电压波形图

4.2 实验结果

为了进一步验证所提控制策略的正确性。在仿真的基础上搭建了一台1.7 kw的实验平台。控制器采用TI公司的TMS320F28335。交流侧电压为120 V，直流侧输出电压为300 V，直流侧负载电阻为60 Ω，其余主电路参数与仿真参数相同。图15为三种控制方法下的样机的实验波形。

图15 采用三种控制方案整流器实验波形图

由图15可知，采用PR控制的波形THD为5.34%，重复控制的波形THD为4.12%，复合控制下的波形THD为3.05%。复合控制有更好的谐波抑制性，同时从实验波形可以看出，采用复合控制的控制策略具有更加优良的输出特性。

5 结束语

为了减少交流侧电流谐波对电网的影响，提出了基于重复和PR控制的PWM整流器复合控制策略。该策略结合了PR和重复控制两者的优点。既保留了PR控制能够很好实现无静差跟踪[9]，并且对于电流跟踪有很好的动态响应的优点，又结合了重复控制能够很好抑制电网谐波干扰[10]，使交流侧电流波形质量高的优点。实验对比了PR控制，重复控制和复合控制，最终实验表明基于PR和重复控制的复合控制输出波形稳态精度高，波形质量好，因此复合策略是更为理想的控制策略。

[1] 张志文, 彭立英, 孙树波,等. 单相PWM整流器电流解耦双闭环控制方法研究[J]. 电源技术, 2015, 39(11):2524-2526.

[2] 赵涛, 王吉虎, 黄家才,等. 基于PI和重复控制三相并网逆变器的设计[J]. 电力电子技术, 2015, 49(1):20-22.

[3] 关向武. PWM整流器的控制方法研究与设计[D]. 东北大学, 2011.

[4] 栗晓政, 孙建平, 甄晓亚,等. 基于PR与PI联合控制策略的光伏并网系统直流注入抑制技术[J]. 电力自动化设备, 2013, 33(3):118-122.

[5] 张胜权. 三相光伏并网型逆变器控制策略研究[D]. 哈尔滨工程大学, 2013.

[6] 梁利民, 粟时平, 朱镜儒. 基于三相光伏并网系统的比例谐振重复控制研究[J]. 电力科学与工程, 2014,30(6):66-72.

[7] 何亮, 王劲松. 三相PWM逆变器输出LC滤波器设计方法[C]. 中国核动力研究设计院科学技术年报, 2014:33-36.

[8] 周二彪, 晁勤, 常喜强,等. 三相光伏并网逆变器控制策略的研究[J]. 电器与能效管理技术, 2013,29(6):34-40.

[9] 孟建辉, 石新春, 付超,等. 基于PR控制的光伏并网电流优化控制[J]. 电力自动化设备, 2014, 34(2):42-47.

[10] SHE J H, PAN Y, NAKANO M. Repetitive control system with variable structure controller[C]// Advances in Variable Structure Systems-Analysis, Integration and Applications-, IEEE International Workshop on Variable Structure Systems, 2015:273-282.

A Research on Single-phase PWM Rectifiers Based on Compound Repetitive Control and PR Control

Liu Pengfei, Wang Junyan

(Department of Electrical Engineering, Shanghai Jiao tong University, Shanghai 200240, China)

How to reduce the influence of AC side current harmonics upon the power grid is the key point for the control of PWM rectifiers. In view of main causes for occurrence of harmonics, this paper presents a compound control strategy based on repetitive control and PR control. PR control realizes tracking of sinusoidal current with zero steady-state error, while PR completes memory and correction of harmonic disturbance by using its internal model. Furthermore, the single-phase PWM rectifier is simulated on the basis of Matlab. Simulation and experimental results are compared for PR control, repetitive control and compound control, and it is concluded that the compound control strategy can reduce AC side current harmonics, has quick dynamic response, and can better suppress harmonic disturbance of the power grid.

PWM rectifier; proportional-resonant control (PR control); repetitive control; compound control; current harmonics

10.3969/j.issn.1000-3886.2017.02.007

TM422

A

1000-3886(2017)02-0022-04

刘鹏飞(1991-)，男，四川成都人，硕士生，研究方向为电力电子与电力传动。 王君艳(1968-)，女，辽宁大连人，副教授，研究方向为电力电子与电力传动。

定稿日期: 2016-11-19