基于多线圈变压器的DC-DC变换器闭环控制策略

梁永，谢宝昌，蔡旭

(电子信息与电气工程学院风力发电研究中心，上海交通大学，上海 200240)

基于多线圈变压器的DC-DC变换器闭环控制策略

梁永，谢宝昌，蔡旭

(电子信息与电气工程学院风力发电研究中心，上海交通大学，上海 200240)

级联式DC-DC变换器因具备高耐压能力的优势，被广泛应用于高压直流输电。在级联式变换器中，将多个模块中的独立变压器整合为一个共享磁芯回路的多线圈变压器，可自动均衡模块电容电压，降低系统复杂程度。针对基于多线圈的级联式DC-DC变换器提出了一种闭环控制策略，为设计移相闭环控制器，采用周期平均法及小信号动态分析法对系统进行建模，引入校正环节改善了系统的稳态和暂态性能，实现了级联式DC-DC变换器输出电压的稳定控制。最后，在Matlab/Simulink环境中搭建了系统仿真模型，验证了所提级联式DC-DC变换器闭环控制方法的可行性。

双向直流变换；多线圈变压器；周期平均法；小信号模型；PI控制器

0 引 言

高压直流输电是清洁能源应用和国际可再生能源互通发展的关键技术。相比于高压交流输电，高压直流输电具备电缆损耗更低的优势，广泛应用于海上风电和太阳能发电系统[1-2]。然而，高压直流输电系统对开关器件耐压能力要求较高，单个桥式变换电路难以满足电压等级要求，因此高压直流变电环节多采用级联式DC-DC变换器。

双向DC-DC变换器根据电路结构不同可分为隔离式和非隔离式，隔离式变换器能有效地改善电能质量，在输配电系统中得到广泛应用。隔离式变换器的体积和重量主要取决于核心变压器，由于工作于中高频率可以降低变压器的体积和重量，尤其在需要能量双向流动的场合，中高频隔离式双向DC-DC变换器可以大幅度降低制造和运输成本[3]，因而具有很高的研究价值。

隔离式中高功率DC-DC变换器的关键技术主要包括：桥式电路的拓扑结构、控制方法以及隔离变压器的设计。DC-DC变换器采用移相调制方法时，通过调节变压器原、副边的方波移相角，可以定量调节功率双向流动。DC-DC变换器的控制策略的研究主要集中在减小损耗及功率回流控制[4-5]和均衡模块电压控制[6-7]。但均衡模块电压的控制环节增加了系统的复杂程度和成本，阻碍了DC-DC变换器的广泛应用。而当变压器采取多线圈设计方法时，模块电容电压可自动均衡，这减小了系统的设计难度[8-9]。与传统工频变压器设计方法不同，大功率中高频变压器的参数设计主要体现在磁芯的选材与几何参数的确定[10]，分析计算变压器模型时要重点考虑变压器在交流工况下的功率损耗[11]。

本文针对基于多线圈变压器的级联式DC-DC变换器提出一种闭环控制方法。该变换器采用多线圈中频变压器，能有效地实现各模块电容电压的自动均衡；单元模块两端采用半桥电路，降低了开关器件的数量，有效减小了系统的开关损耗。在采用周期平均法与小信号动态分析方法建模的基础上，设计了移相闭环控制器，实现输出电压值的稳定控制。最后，在MATLAB/Simulink环境中搭建了该级联式变换器系统的仿真模型，验证了所提级联式DC-DC变换器及其闭环控制方法的可行性。

1 变换器工作原理

本文研究的DC-DC变换器系统结构如图1所示，原端k个模块，副端l个模块。该系统用多线圈变压器替代多个模块中的独立变压器，能有效抑制直流电容充电电流和直流电源的电流纹波，自动实现各模块电容电压均衡。

图1 基于多线圈变压器的 DC-DC变换器

多线圈变压器高低压绕组分别由多个线圈组成，这些线圈共享同一个磁芯回路。多线圈变压器的同侧各线圈实际为串联结构，其电气参数计算方法原理与高低压绕组圈变压器一致，在计算漏感及损耗时要考虑多线圈结构带来的影响。

基于多线圈变压器的级联式变换器控制电路由多个半桥控制单元串联组成，每个半桥控制单元单独与变压器线圈连接。为了更直观的分析半桥控制拓扑结构的工作原理，下面分别取原端和副端的第一个单元进行分析。

图2 DC-DC变换器 原副端单元结构

图2所示为双向半桥变换器原副端单元结构，电容C11、C12和电容C21、C22是支撑电容，分别对输入电压U1/k和输出电压U2/l分压，电感L为变压器漏感与串联电感之和，参数设计阶段可选取电容值使电容电压波动范围最小化。

当输入端的奇数序号开关管导通时，桥路电压ua为正；偶数序号开关管导通时，桥路电压ua为负，绝对值近似为U1/k的一半。同理，输出侧在开关管轮流导通时呈现相同的规律，桥路电压ub折算到一次侧与输入端桥路电压ua形成的电压差加在电感L上，使电感电流周期性变化。采用移相调制方法，定义移相比D为开关管Q11、Q12与开关管Q21、Q22的导通时间差与半个周期Ths的比值，电感电流在电压的作用下周期变化，如图3所示。

图3 移相调制工作原理

由图3可知，电感电流分段线性，经分析四个阶段里电感电流表达式分别如下:

(1)

(2)

(3)

(4)

2 变换器小信号动态建模

实际运用阶段，可根据待变换的电压等级以及变换单元可接入的电压范围设计变换器单元个数，本文研究两组变换单元串联系统的建模及控制方法，即k=l=2。将两组变换器单元串联并连接到多线圈变压器得到级联式DC-DC变换器，假设负载为纯电阻，功率正向流动。图4和图5分别为输出侧偶数、奇数序号开关管开通时的节点电流关系图，对电路进行分析，当负载端偶数序号开关管开通时，奇数序号开关管及其反并联二极管等效为断路，流过奇数序号电容电流即为负载电流，而当奇数序号开关管开通时，流过偶数电容电流为负载电流，在这两种状态下对电路列写节点电流方程如下:

(5)

(6)

当iL1=iL2=iL，引入电容电流与变换器输出电压的关系式:

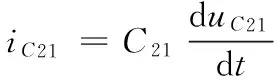
(7)

综合式(5)、(6)、(7)可得级联式变换器输出电压的状态方程如下:

(8)

若C21=C22，等效电容Ceq=1/(1/C21+ 1/C22)=C21/2，负载电流iR=u2/R，即：

(9)

采用周期平均法，用代数式的周期平均值表示电压u2微分值如下:

(10)

根据第1节的分析，将式(1)-(4)电感电流iL(t)的表达式代入式(11)得:

(11)

图4 开关Q21、Q23关断；Q22、Q24开通节点电流

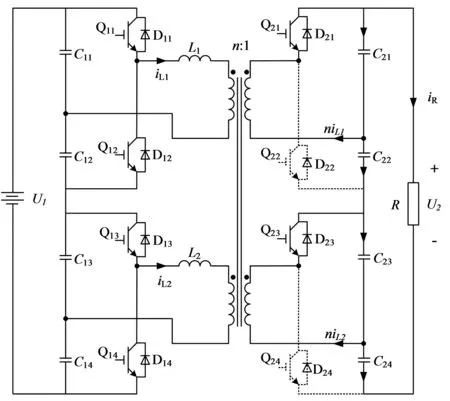
图5 开关Q21、Q23开通；Q22、Q24关断节点电流

小信号模型以稳态点处的扰动与由此引起的输出量的变化的关系为基础，在进行小信号模型的仿真时，系统应已经达到稳定状态，然后根据各变化量与输出变化量之间的传递函数来进行扰动及稳定性分析。假设输入电压不变，引入输出电压和移相比的小信号交流量:

(12)

将(12)代入方程(11)得稳态输出电压与移相比的关系式及输出电压交流量的状态方程式如下:

(13)

(14)

因此，输出电压与移相比的传递函数为:

(15)

同时，这也是级联式DC-DC变换器模型原有部分的传递函数，表示开环系统的属性。

3 系统校正及运行分析

直流变换器在具体投入应用时，良好的电压稳定能力是必不可少的。为实现输出电压的稳定，对系统进行闭环控制，同时引入校正环节，改善控制系统的性能。

下面通过模型仿真给出控制器的设计方法，表1是级联式DC-DC变换器模型的电路参数。

表1 级联式DC-DC变换器模型电路参数

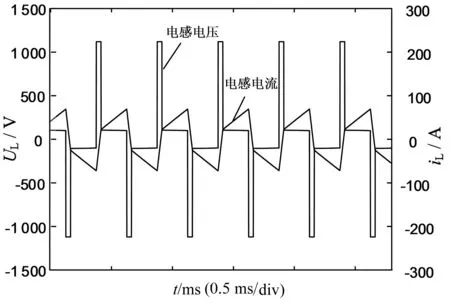
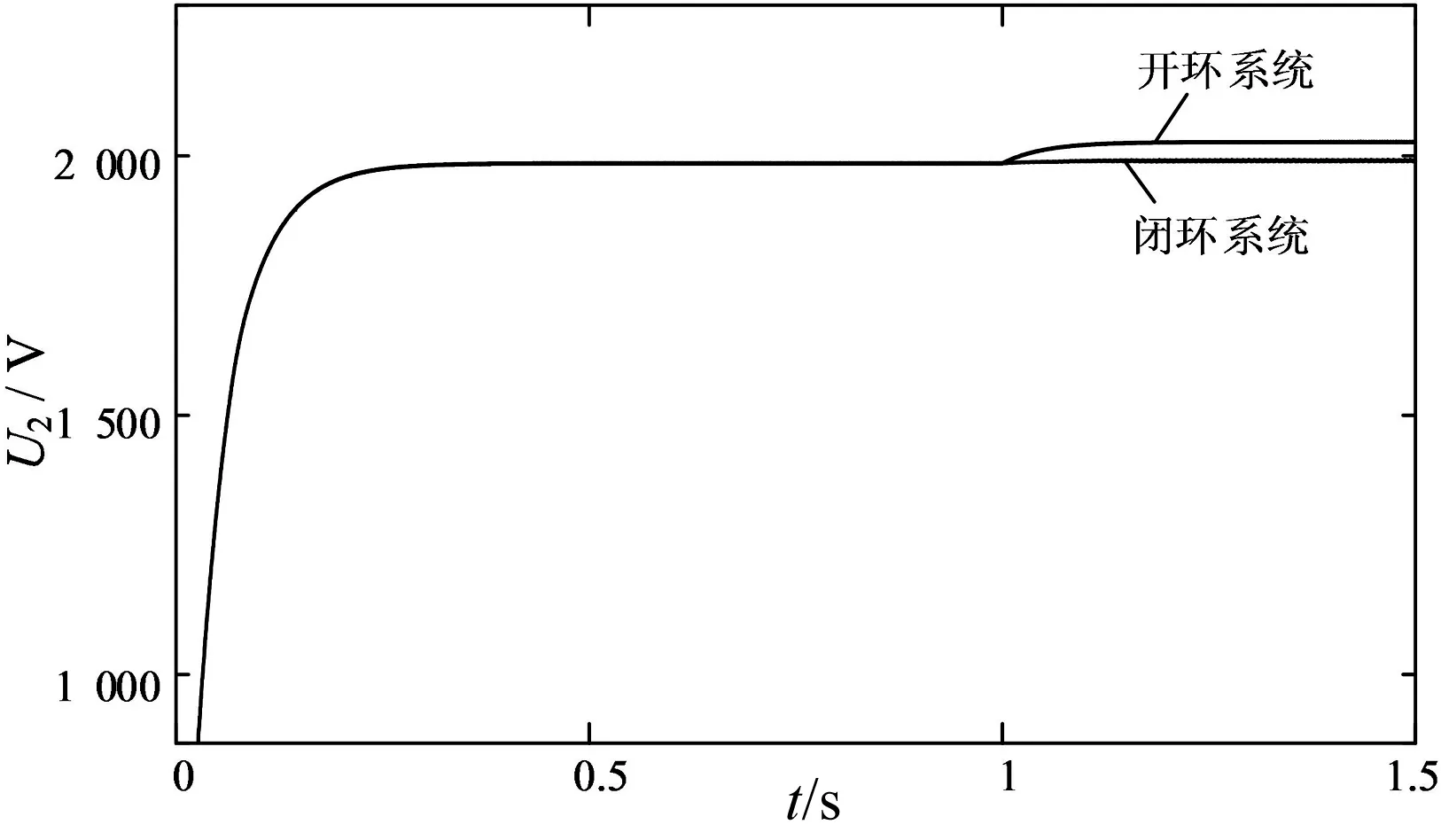
根据式(13)中稳态电压与移相比的关系式可知当移相比为0.5时，该变换器可输出的最大电压为3 750 V，由实际输出电压计算得稳态工作的移相比D1=0.158 4或D2=0.841 6，当移相比0

加入校正环节前的开环传递函数为:

(16)

校正环节的设计可以采用时域法和频域法，在频域法中最有影响力的方法是波特图法，下面采用波特图法设计补偿网络。通过第2节的分析可知，输出电压与移相比的传递函数为一阶惯性环节，在系统中引入PI控制器可实现系统稳态和暂态性能的改善。一般的，PI控制器的传递函数可表示为式(17)，其中KP和KI分别为比例系数和积分系数。

(17)

引入PI控制器后，回路增益函数的幅频曲线如图6所示，增益交接频率处的斜率为-20 dB/dec，相角裕度为90度，满足稳定性要求。

图6 加入校正环节前后的波特图

系统达到稳态后，电感两端的电压电流波形如图7所示，从图中可以看出，电感两端电压基本对称，电容电压的波动对电感电压的影响可忽略不计。

图7 系统稳态下电感电压及电流波形

图8 加入扰动后闭环与开环系统的输出电压波形

图8所示为在t=1 s时加入0.5% 扰动后的开环闭环系统输出电压波形对比效果图，可见在加入闭环控制及校正环节后，输出电压在电路出现扰动后，电压值仅呈现微小的变化，基本保持稳定，因而，针对基于多线圈变压器的级联式DC-DC变换器，所设计的控制系统具有良好的稳压能力。

4 结束语

本文提出了一种基于多线圈变压器的级联式DC-DC变换器输出电压的控制方法。该级联式DC-DC变换器采用多线圈中频变压器，将变换器单元串联提高了系统变压等级，通过改变移相角调节输出电压的大小。应用周期平均法及小信号动态分析方法对级联式DC-DC变换器建模，为实现输出电压稳定采取闭环控制方法，引入校正环节以改善系统的稳态和暂态性能。在

MATLAB/Simulink环境中搭建了系统的仿真模型，仿真结果表明，稳态系统在加入扰动的情况下，输出电压保持恒定，验证了本文所提控制策略的可行性及环路设计的正确性。

[1] ZHANG Y, ADAM G, FINNEY S, et al. Improved pulse-width modulation and capacitor voltage-balancing strategy for a scalable hybrid cascaded multilevel converter[J]. IET Power Electronics, 2013, 6(4): 783-797.

[2] HU Y, ZENG R, CAO W, et al. Design of a modular, high step-up ratio DC-DC converter for HVDC applications integrating offshore wind power[J]. IEEE Transactions on Industrial Electronics, 2016, 63(4): 2190-2202.

[3] STEINER M, REINOLD H. Medium frequency topology in railway applications[C]. Power Electronics and Applications, 2007 European Conference on. IEEE, 2007: 1-10.

[4] PENG F Z, LI H, SU G J, et al. A new ZVS bidirectional DC-DC converter for fuel cell and battery application[J]. IEEE Transactions on Power Electronics, 2004, 19(1): 54-65.

[5] 赵彪, 于庆广, 孙伟欣. 双重移相控制的双向全桥 DC-DC 变换器及其功率回流特性分析[J]. 中国电机工程学报, 2012, 32(12): 43-50.

[6] 陈武, 阮新波, 庄凯. 输入串联输出并联 DC/AC 逆变器系统的控制策略[J]. 中国电机工程学报, 2010, 30(15): 16-23.

[7] LU Y, XING Y, WU H. A PWM plus phase-shift controlled interleaved isolated boost converter based on semi-active quadrupler rectifier for high step-up applications[J]. IEEE Transactions on Industrial Electronics, 2016, 63(7): 4211-4221.

[8] 谢宝昌. 多线圈单相中频方波变压器的双向高压DC/DC控制方法: 103944401[P]. 2016-05-04.

[9] 郑天奇, 谢宝昌, 蔡旭. 单相多线圈中频变压器 DC/DC 控制方法研究[J]. 电气自动化, 2015, 37(3): 61-63.

[10] VILLAR I, GARCIA BEDIAGA A, VISCARRET U, et al. Proposal and validation of medium-frequency power transformer design methodology[C]. 2011 IEEE Energy Conversion Congress and Exposition. IEEE, 2011: 3792-3799.

[11] HURLEY W G, GATH E, BRESLIN J G. Optimizing the ac resistance of multilayer transformer windings with arbitrary current waveforms[J]. IEEE Transactions on Power Electronics, 2000, 15(2): 369-376.

A Closed Loop Control Strategy for the DC/DC Converter Based on the Multi-coil Transformer

Liang Yong, Xie Baochang, Cai Xu

(Wind Power Research Center, College of Electronic Information and Electrical Engineering, Shanghai Jiao tong University, Shanghai 200240, China)

Cascaded DC-DC converters are widely applied in HVDC power transmission because of their strong voltage endurance capability. In the cascaded converter, independent transformers in several modules are integrated into a multi-coil transformer sharing the loop of the magnetic core, so that the capacitor voltages of the modules can be equalized automatically and the system is made less complex. With respect to multi-coil-based cascaded DC-DC converters, this paper presents a closed-loop control strategy. In order to design a phase shift closed loop controller, we use the periodic average method and small-signal dynamic analysis method to establish a model for the system. Furthermore, a correction link is introduced to improve steady-state and transient performance of the system, and steady control of the output voltage of the cascaded DC-DC converter is achieved. Finally, a system simulation model is built in Matlab / Simulink environment, and the feasibility of the proposed closed-loop control method for the cascaded DC-DC converter is verified.

bi-directional direct current transfer;multi-coil transformer; periodic average method; small-signal model;PI controller

10.3969/j.issn.1000-3886.2017.02.002

TM432

A

1000-3886(2017)02-0005-04

梁永(1991-)，男，江苏人，硕士生，上海交通大学电气工程系，主要从事电机与电器研究。

定稿日期: 2016-12-21