计及供电方收益的分时电价优化

薛太林， 许倩

(山西大学, 山西 太原 030013)

计及供电方收益的分时电价优化

薛太林， 许倩

(山西大学, 山西 太原 030013)

峰谷分时电价；负荷转移率；用户响应；遗传算法；时段划分

0 引 言

峰谷分时电价是电力需求侧管理[1]的重要措施之一，在国内外已经得到广泛应用。为节约投资和运行成本，考虑到分时电价可能带来的利益，用户在用电方面会做出一定响应，负荷曲线也会跟着发生一定变化。合理分时电价下的用户响应能够有效均衡负荷，改善负荷曲线，并以此缓解电网在用电高峰时期电力供应紧张的问题。

目前针对峰谷分时电价的研究主要集中于峰谷时段的划分[2,3]和用户响应模型[4-7]两个方面。传统的划分方法根据历史曲线及经验，缺乏科学的理论依据。文献[8]采用模糊聚类方法进行峰谷时段划分，利用尖峰时刻电价对用户的影响，建立了基于需求价格弹性矩阵的用户响应模型。文献[9]87提出负荷转移率的概念，并用负荷转移率曲线来反映用户对电价的响应，但没有提出相应的分时电价响应模型。文献[10]基于需求价格弹性矩阵，构建分时电价的用户响应模型，并以削峰填谷为目标，建立了峰谷分时电价的非线性约束的优化模型，但只是在响应范围内，忽略了用户对电价的变化存在一个无响应区间；用谷时段边际成本约束峰平谷各时段电价，只能保证谷时段的供电成本，并不能保证供电方在实施分时电价后也能获得利益。文献[11]建立优化模型时，从用电方式和电费支出两方面考虑用户的满意度问题，保证了用户方的利益,但忽略了供电方的利益。文献[12]计及供电购电风险，以收益最大化为目标，却忽略了用户的受益问题。

本文采用负荷转移率来建立用户响应模型，在保证用户和供电方两边利益为约束条件下，以最小峰谷差为目标，构建峰谷分时电价优化模型。应用遗传算法进行求解，并分析电价优化后的用户响应效果。通过算例分析，表明该模型能有效改善负荷曲线，并分析改变时段划分对用户响应的影响。

1 用户响应模型

1.1 用户响应曲线及数学模型

分时电价下的用户响应行为主要体现在电价发生变化时，用户用电负荷的改变。合理的用户响应模型，能够准确反映负荷随电价的变化情况。用户响应建模是研究分时电价的基础和前提，也是实现电价优化的关键。本文采用基于消费者心理学[13]建立用户的负荷响应模型。用户对一定范围的电价作出响应(即响应区)，在响应范围内，用户响应的程度大小与电价的变化大小有关；当电价的变化值小于这个范围，用户基本上没有反应(即死区)；当变化值大于这个范围，用户响应达到一个饱和状态(即饱和区)，不再继续响应。利用负荷转移率对这一响应过程进行描述，并假定负荷从高电价时段向低电价时段的转移量与电价差值成比例关系。根据上述描述，可将基于负荷转移率的用户响应模型近似拟合成分段线性函数，如图1所示。用横坐标表示i时段与j时段的电价差值，纵坐标表示用户i时段到j时段的负荷转移率。

图1 i时段到j时段的用户响应曲线

(1)

Δij=pi-pj

(2)

受用户行业类型、用电特性、电费占用户总成本的比例等因素的影响，不同类型的用户对电价的响应程度不同。对相应程度高的用户，差别较小的分时电价就能够达到理想效果，而对响应程度低的用户，则差值较高的峰谷电价才能够达到预期效果，但最终都体现在死区阈值、线性段斜率和饱和区阈值这三个参数的不同。对于参数的求取，一般都是根据社会调查数据采用线性回归法后确定，但是不能充分体现用户的响应情况。文献[9]90利用每次实施分时电价后的数据，逐次对相关参数进行了辨识和更新，动态修正负荷转移率曲线，准确求取死区阈值和饱和区阈值的大小。

1.2 各时段的拟合负荷

基于上述描述可以得到，峰时段到平时段、峰时段到谷时段以及平时段到谷时段三种用户响应模型。由此推出，实施分时电价后用户的拟合负荷，其表达式为：

(3)

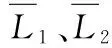
T1+T2+T3=24

(4)

假定负荷从某一时段转移到另一时段的用电量在时间轴上均匀分布。由于峰平谷各时段的长度可能不同，所以在计算拟合负荷时候，负荷转移量需要乘上代表时段长度比值的系数，得到下式：

(5)

其中n1、n1、n3分别表示峰平谷各时段的时间长度。

2 分时电价优化模型

2.1 目标函数

实施峰谷分时电价的目标是为缓解系统在高峰期的用电紧张，调整负荷曲线，提高系统负荷率和运行效率。所以，将峰谷差最小设为目标函数：

min(maxLt-minLt)

(6)

2.2 约束条件

(1)用户收益

分时电价实施前后用户的日用电量分别为：

实施前：

(7)

实施后：

(8)

式中Q1、Q2、Q3分别表示峰谷分时电价实施后，用户在峰时段、平时段、谷时段的用电量。分时电价实施前电网的平均售电电价为p0，得到分时电价实施前后用户的电费支出：

实施前：

E0=p0·Q0

(9)

实施后：

(10)

用户在响应分时电价时可能会调整原有的舒适用电方式，改变用电习惯以节约成本。为激励用户积极参与响应，在分时电价实施后，应该保证用户的用电费用不高于实施之前，即满足：

ETOU≤E0

(11)

(2)供电方收益

峰谷分时电价实施后，要保证供电方的成本与合理利润。供电方的利润率为：

(12)

合理利润的约束范围：

rmin≤r≤rmax

(13)

式中r表示为供电公司的利润率，s0为供电公司的购电电价，Lossi为第i时段的网络损耗[14]，其费用由供电方负责；rmin、rmax分别为利润率的最小值和最大值。

(3)电价限制

为了避免分时电价后，出现峰谷倒置，峰谷错位或响应不足的情况，一般峰时段电价较高于平时段电价，谷时段电价低于平时段电价，而且峰谷电价比要有一定的范围限制。公示表达如下：

p1>p2>p3

(14)

(15)

式中k1，k2为限制峰谷电价比的常数。在我国，峰谷电价比的取值一般在2～5之间[15]。在本文中取k1=2,k2=5。

3 模型求解

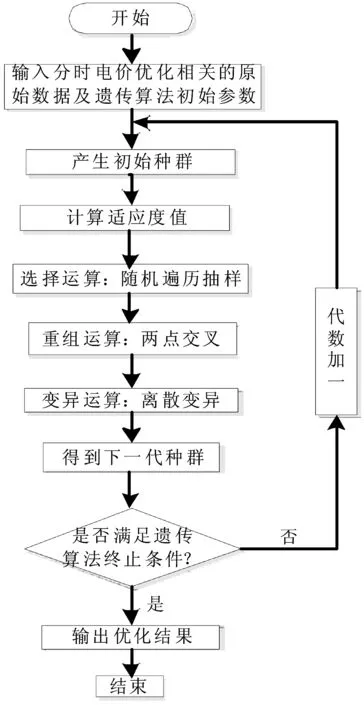
图2 分时电价优化流程图

综合(6)式、(11)—(16)式可得到关于峰谷分时电价的优化模型。求解程序流程图如图2所示。

用遗传算法进行优化时，采用二进制编码，二进制位数为5，设置种群个体数目NIND为100，最大遗传代数MAXGEN为160，代沟GGAP为0.9，两点交叉概率Pc为0.5，离散变异概率Pm为0.1。

4 算例分析

4.1 原始数据

以地区实际负荷数据为例，验证该模型的有效性。时段划分如下：峰时段为：8:00—11:00，17:00—21:00；平时段为：11:00—17:00，21:00—23:00；谷时段为：23:00—次日8:00。其日负荷数据如表1所示。

表1 日负荷数据

用户响应负荷转移率曲线的相关参数如表2所示。实施分时电价前，电网平均电价p0=0.475元/kW·h；电网的购电电价s0=0.425元/kW·h；网络损耗取Lossi=10%，给定利润率的限制范围：rmin=1%,rmax=3%。

表2 负荷转移率曲线的相关参数

4.2 优化结果分析

在MATLAB环境下进行多次仿真运算后取平均值，得到的电价优化结果为：p1=0.615元/kW·h，p2=0.457元/kW·h，p3=0.19元/kW·h，峰谷电价比为3.12。分时电价实施前后的负荷曲线对比如图3所示。用户响应效果如表3所示。

图3 分时电价实施前后的负荷对比曲线

优化前后最大负荷/MW最小负荷/MW峰谷差/MW负荷率优化前42251880225575.11%优化后38772244163383.46%变化量-348364-6228.35%

由上述数据比较可知，实行分时电价后，最大负荷降低了348 MW，最小负荷增加了364 MW，峰谷差由2 255 MW降到了1 633 MW，负荷率提高到83.46%，而且用户的日用电费用减少了2 782元，供电方也有2.31%的利润。从图中可以看出，实施峰谷分时电价可以有效调整负荷曲线，实现削峰填谷。

4.3 改变时段划分对分时电价的影响

图4 时段优化后实施分时电价的负荷曲线

根据原始负荷曲线特点，对时段进行优化，得到的优化结果：9:00—11:00，17:00—21:00，共6小时；平时段为：7:00—9:00，11:00—17:00，21:00—23:00，共10小时；谷时段为：23:00—次日7:00，共8小时。在此时段划分的基础上求解优化模型，得到峰时段电价为0.639元/k W·h,平时段电价为0.443元/k W·h，谷时段电价为0.186元/kW·h。优化前后的负荷曲线对比如图4所示。

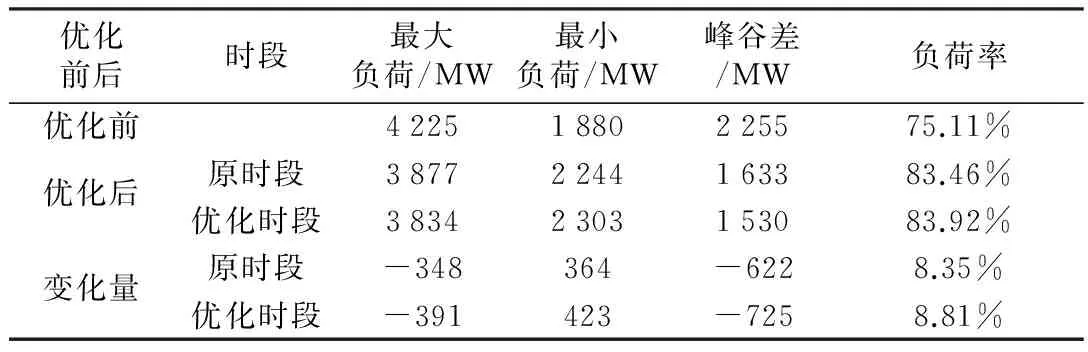
表4 时段优化后的需求响应效果

由表4用户响应效果情况对比可知，时段优化后实施分谷电价，各项性能指标与原时段相比都有所提高。最大负荷变化量由348 MW增加为391 MW；最小负荷变化量由364 MW增加为423 MW，峰谷差变化量由622 MW增加为725 MW，负荷率较之前提高了0.46%。用户的用电费用较之前也节省了427元，供电方也有1.4%的盈利。合理的时段划分能够使实施分时电价达到更好的效果，消峰效果更好，负荷曲线更加平稳。

5 结束语

本文基于负荷转移率建立用户响应模型，以削峰填谷为目标，考虑供电和用电两方利益，建立了峰谷分时电价优化模型，并通过算例说明该算法的有效性。由于不同地区、不同行业的用户负荷特性和对电价的响应程度不同，所以需要根据对不同类型的用户负荷特性进行峰谷时段划分并采用分类负荷峰谷电价，才能充分挖掘用户的削峰能力，达到更好的效果。

[1] 张钦,王锡凡,王建学,等. 电力市场下需求响应研究综述[J]. 电力系统自动化, 2008, 32(3): 97-106.

[2] 林旻, 朱艳卉, 胡百林.基于供电成本的峰谷时段划分及分时电价研究[J]. 华东电力, 2005, 33(12): 90-91.

[3] 程瑜, 翟娜娜. 基于用户响应的分时电价时段划分[J]. 电力系统自动化, 2012, 36(9): 42-46.

[4] DE SA FERREIRA R，BARROSO L A，ROCHINHA LINO P,et al.Time-of-use tariff design under uncertainty in price elasticities of electricity demand：a stochastic optimization approach [J]. IEEE Trans on Smart Grid，2013, 4(4): 2285-2295.

[5] 孔祥玉, 杨群, 穆云飞,等. 分时电价环境下用户负荷需求响应分析方法[J]. 电力系统及其自动化学报, 2015, 27(10): 75-80.

[6] 刘继东, 韩学山, 韩伟吉,等. 分时电价下用户响应行为的模型与算法[J]. 电网技术, 2013, 37(10): 2973-2978.

[7] 刘辉舟, 高飞, 胡小建,等. 分时电价模型优化方法研究[J]. 电力需求侧管理, 2013, 15(4): 11-15.

[8] 周博, 王博, 高松,等 基于用户响应的分时电价模型研究[J]. 智能电网, 2016, 4(3): 307-311.

[9] 阮文骏, 王蓓蓓, 李扬,等. 峰谷分时电价下的用户响应行为研究[J]. 电网技术, 2012, 36(7): 86-93.

[10] 李春燕, 许中, 马智远. 计及用户需求响应的分时电价优化模型[J]. 电力系统及其自动化学报, 2015, 27(3): 11-16.

[11] 丁伟, 袁家海, 胡兆光. 基于用户价格响应和满意度的峰谷分时电价决策模型[J]. 电力系统自动化, 2005, 25(20): 10-14.

[12] 崔强，王秀丽，曾平良,等.调峰约束下考虑风电消纳的多目标尖峰电价决策模型[J]. 中国电机工程学报,2015,35(11): 2662-2669.[13] 罗运虎, 邢丽冬, 王勤,等. 峰谷分时电价用户响应模型参数的最小二乘估计[J]. 华东电力, 2009, 37(1): 67-69.

[14] 陈沧杨, 胡博, 谢开贵,等. 计入电力系统可靠性与购电风险的峰谷分时电价模型[J]. 电网技术, 2014, 38(8): 2141-2148.

[15] 王超. 基于分时电量综合响应度的峰谷电价优化模型研究[D]. 华北电力大学:北京, 2010.

Optimization of Time-of-use Electricity Price Taking into Account Profit of the Power Supplier

Xue Tailin, Xu Qian

(Shanxi University, Taiyuan Shanxi 030013, China)

Peak-valley time-of-use electricity pricing is an important means for power demand side management. Driven by interest, the user will respond to the changing price and automatically adjust the time and amount of its electricity consumption, so that peak shaving and valley filling of the load curve is realized to attain the purpose of investment delay and improvement of stability and economy of grid operation. Aiming at minimization of peak-valley difference and confined by user interest and power supplier's reasonable profit, we use load transfer rate for simulation of price response action to establish a time-of-use price optimization model, which is solved in the genetic algorithm. Finally, user response to time-of-use price is analyzed through calculation examples, and the effectiveness of the model and approach is verified. Furthermore, influence of different time segment division upon user response is analyzed.

peak-valley time-of-use electricity price; load translating rate; customer response; genetic algorithm; time segment division

10.3969/j.issn.1000-3886.2017.02.009

TM792

A

1000-3886(2017)02-0029-04

薛太林(1966-)，男，山西新绛人，教授，研究方向为电能质量检测与控制。 许倩(1990-)，女，山西运城人，硕士生，从事电力需求侧管理方面研究。

定稿日期: 2016-12-09