构造法在高中数学解题中的应用
2017-04-21浙江省绍兴市上虞区丰惠中学王东芬
☉浙江省绍兴市上虞区丰惠中学 王东芬
构造法在高中数学解题中的应用
☉浙江省绍兴市上虞区丰惠中学 王东芬
解题的过程实际上就是利用已有知识和条件来求解未知参数的过程,但是在实际的数学解题过程中不可避免地会遇到缺乏解题条件或者解题条件不合理等问题,此时如果合理应用构造法,那么可以快速达到求解的目的.因此,如何才能有效地将构造法应用于高中数学解题值得深入探讨.
一、构造法的基本原理
顾名思义,构造法就是按照已知方式或者经过一些步骤将某些比较抽象的问题直观化、形象化,进而再按照一般方式进行求解的过程.通常而言,我们在解题时常常伴随着一种内在的思维定式情况,即按照正面思考顺序,结合已知条件来探讨问题的求解思路,数学问题的求解也不例外.但是在实际数学问题的求解过程中却常常会因该种思维定式而无法顺利解题,此时如果可以合理采用逆向思维来思考和求解数学问题,那么往往可以达到“绝处逢生”的目的,构造法实际上就是基于该种思想的一种方法.而就构造法在数学问题求解中的具体应用而言,其主要是要求我们在无法按照传统求解思路和理念解决问题的情况下,去换个角度来探讨已知条件和问题以及未知参数等之间的关系,进而借此来建立一种新型问题来快速求解问题.从根本上来讲,构造法具有创造性、不固定性、多样性和灵活性等特性,关键在于“构造”二字.
二、构造法在高中数学解题中的应用
构造法在高中数学解题中的应用范围比较广,涉及到高中数学几何知识、数列知识、函数知识以及不等式知识等诸多方面.而就构造法在解题中的具体应用而言,其主要包括如下几个方面.
1.构造方程法
构造方程法是高中数学中常见的一种解题方法,是大多数高中生比较熟悉的一种解题方法.实际上,函数和方程二者之间本身具有很强联系性,其中构造方程就是充分借助题干信息中的数量关系和结构特征等来假设构成一个或者几个等量方程关系式,进而借助相应等量方程关系式的构建来达到简化解题思路的目的,同时也可以使学生在运用构造方程解题时培养和提升他们的思维能力与观察能力.
例1已知(m-n)2-4(n-x)(x-m)=0,试求证m,n,x为等差数列.
分析:针对该道数学试题的求解,可以借助构造方程法来将题干信息中的有关条件和结论进行有效结合,这样可以实现对题干信息简单化、形象化,有助于更好地构建求解问题的方程.而如果按照传统的求解方法,那么不仅费时费力,最终学生可能也无法达到求解问题的目的.
解:构建方程(n-x)t2+(m-n)t+(x-m)=0,①
令F(t)=(n-x)t2+(m-n)t+(x-m).
由题意可知,F(1)=0,则可知所构建方程①中实数根相等,那么可由(n-x)t2+(m-n)t+(x-m)=0解得t=1,这也意味着方程中两个实数根取值均为1.然后由韦达定理即可求得m+n=2x,这样即可证明m,n和x是等差数列.
如此一来,通过借助构造方程法,有助于将相应的数学问题简单化,可以快速解答有关的数学题目,增强解题效果.
2.构造函数法
同构造方程法类似,高中数学中的函数知识和方程之间具有紧密联系.构造函数法的合理应用,可以培养和提升学生的解题能力,尤其适用于几何类型和代数类型数学题干信息的求解中来.在实际的数学题目求解过程中,可以将某些数学问题转化成一些形式比较简单的函数形式,有助于达到简化求解过程,提高解题准确度的目的,同时也有助于培养学生的创造性思维.

3.构造向量法
向量作为高中数学的重要组成部分,也是高考数学学科考查的重点内容.实际上,向量既可以进行代数运算也可以进行几何运算.借助构造向量法的合理应用,可以把有关问题从数过渡到形,有助于增强某些问题的直观性和形象性,帮助学生更好地解决有关的向量问题.特别是针对不等式的结构特征,如m1m2+n1n2,此时借助向量数量积即可来表示相应的数学题干信息,从而可以将原来的不等式适当变形为原不等式的证明提供新的方法.这样学生不必再进行烦琐的计算和复杂的论证,只需要简单论证即可.
分析:该题是一道典型的函数题,采用传统解题方法需要进行分类讨论,计算烦琐性比较大,但是如果引入向量方面的知识,构造向量方面的有关式子,那么可以达到简化该题,降低解题难度的效果.

4.构造图形法
纵观高中数学学科中的知识,数形结合法是常见的一种解题方法,构造符合题意的图形,可以将某些文本描述过于烦琐、复杂的数学知识精简化、直观化,有助于增强问题求解的形象化,可以使我们更加便捷地求解有关数学问题,同时也可以使我们在此过程中了解、学习和掌握数形结合方面的重要解题思想和能力.而构造图形法的最直观体现就是数形结合法的应用,其是高中数学学习过程中至关重要的一种解题思想,往往可以使某些抽象、繁杂的数学知识直观化、形象化、简单化,从而有助于我们更好地求解有关的数学问题.
例4已知直线l1:4x-3y+6=0和直线l2:x=-1,抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是().

解析:如图1所示,记抛物线y2=4x的焦点为F,则F(1,0),注意到直线l2:x=-1是抛物线y2=4x的准线,于是抛物线y2=4x上的动点P到直线l2的距离等于|PF|,问题即转化为求抛物线y2=4x上的动点P到直线l1:4x-3y+6=0的距离与它到焦点F(1,0)的距离之和的最小值,结合图形可知,该最小值等于焦点F(1,0)到直线l:4x-3y+6=0的距离d==2.故选A.
1

图1
由此可知,作出相应的直线图形,可以使我们直观地确定待求问题的解题关键所在,不仅有助于加快解题速度,同时也可以培养我们逻辑思维能力.
例5已知点M(3,5),在y轴和直线y=x上分别找一点P和N,使得△MNP的周长最小.
分析:作点M(3,5)关于y轴和直线y=x的对称点M1,M2,则|MP|=|M1P|,|MN|=|M2N|,所以△MNP的周长等于|M1P|+|PN|+|M2N|,当且仅当M1,M2,P三点共线时取最小值,所以点P,N应为直线M1M2和y轴与直线y=x的交点.
解:作点M(3,5)关于y轴和直线y=x的对称点M1,M2,则点M1,M2的坐标分别为(-3,5),(5,3),具体如图2所示.

图2
由此可知,通过构造图形法的合理应用,就可以利用对称思想为线段找到了“替身”,从而将问题转化为两点之间线段最短的问题,那么相应的求解难度将大大降低.
除了应用题计算之外,构造图形法也可以用于选择题的求解.借助构造图形法的合理应用,可以帮助我们快速求解某些选择题,而不再需要烦琐的大量计算,同时计算准确率也比较高,具有很强的应用价值.
例6已知0<a<1,则方程a|x|=|logax|的实根个数为().
A.1B.2
C.3D.1或2或3
解析:判断方程的根的个数就是判断y= a|x|与y=|logax|图像的交点个数,画出两个函数图像(如图3所示),易知两图像只有2个交点,所以方程有2个实根,故选B.
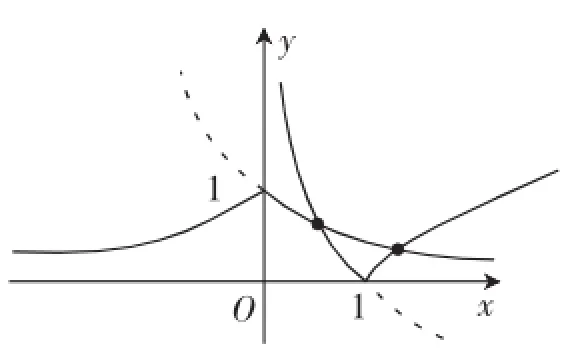
图3
例7函数f(x)=2x+x3-2在区间(0,1)内的零点个数是().
A.0B.1C.2D.3
解析:设y1=2x,y2=2-x3,在同一坐标系中作出两函数的图像(如图4所示),可知B正确.

图4
如果针对例7采用常规的解题方法,相应的步骤为:因为f(0)=1+0-2=-1,f(1)=2+23-2=8,即f(0)·f(1)<0且函数f(x)在(0,1)内连续不断,故f(x)在(0,1)内的零点个数是1.
由此可知,通过借助图形,可以使我们无需继续按照常规的函数对比来判断最终结果,只需要借助绘制图形即可得到我们想要的关键信息,可以快速帮助我们找到解决数学问题的方法,提高我们解题能力.
5.构造数列法
等差数列和等比数列均是高中数学中数列章节的重要内容,本身包含着许多数学性质,是高中数学教材中学习的重点内容和高考的热点内容.在解决相关高中数学方面数列问题的过程中,可以引导学生结合相应的题设特征,借助替换和联想等方式来虚构一个等差数列或者等比数列,那么可以借助等差或者等比数列的合理应用来明确相关数学问题的求解要点,这样就可以起到化繁为简、化抽象为具体的作用.
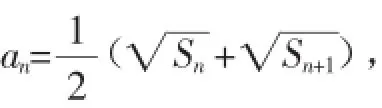
分析:该题是一道典型的数列问题,且已经知道前n项和与数列通项an之间的关系,那么反推Sn的表达式.此时如果采用传统的通项公式求解方法,那么不仅烦琐,也无法直接套用公式,但是如果虚构数列,那么可以建立一个新型的数列来达到求解的目的.
解:当n≥2时,an=Sn-Sn-1,

6.构造解析式法
所谓的构造解析式法实际上就是通过合理构建一个适当的关系式来辅助题目求解,其在解题中的合理应用,有助于大大简化解题思路.而构造解析式法的具体应用模式而言,其主要为结合实际数学问题的特征来合理构建一个与之相关的关系式,然后可以替代原有题干信息中的问题或者简化原有数学问题来彻底解决这些原有的数学问题,从而达到求解数学问题的目的.
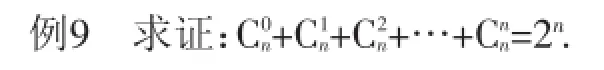

总之,构造法在高中数学解题中的应用范围比较广,可以应用于几何知识、数列知识、函数知识以及不等式知识等诸多类型数学题目求解中.但是为了充分发挥构造法在高中数学题目求解中的积极作用,必须要结合实际的数学问题来合理选择构造法,借助数学求解条件的合理构造来达到简化题目求解的目的.
