一次有关椭圆离心率的探索之旅
2017-04-21江苏省张家港高级中学袁志强
☉江苏省张家港高级中学 袁志强
一次有关椭圆离心率的探索之旅
☉江苏省张家港高级中学 袁志强
众所周知,椭圆离心率是椭圆的重要几何性质,离心率大小决定了椭圆的扁平程度,当离心率e从0经过变化到1时,椭圆内部发生了一系列优美的变化,呈现出许多有趣的性质.将这些有趣的性质设计成一节探究性学习课,让学生探索其中的内在性质,不仅可以加深学生对椭圆几何性质的理解与掌握,还可以培养学生观察问题、分析问题、解决问题的能力,同时在归纳探究中体会椭圆几何性质的奇异美、内在美,在享受美的过程中实现情感体验.通过椭圆及其性质的前期学习,学生对椭圆离心率有了初步的认识,但离心率e从0经过变化到1时,椭圆内部发生的一系列优美的变化,学生却知之较少或不成体系,有待于深化提高.
本课知识目标:在准确理解椭圆离心率与椭圆关系的基础上,掌握离心率e从0经过变化到1时,与椭圆长短轴长、焦距、准线间距离有关的特殊的几何性质;进一步掌握椭圆离心率有关的角度关系、位置关系、弦长最值、焦点弦三角形等问题的处理方法.本课采用的教学方法:“问题诱导—启发讨论—探索结果”及“感知观察—归纳猜证—总结规律”的一种探究性教学方法,注重“引”、“思”、“探”、“练”的结合.基本环节:①课前准备——搭脚手架,②创设情境——研讨交流,③深入探究——解决问题,④联想变形——扩大战果.
第一阶段:课前准备——搭脚手架
课前教师设计一组问题,并将学生分成若干小组.要求学生以小组为单位进行合作预习,预习时若难易直接获得结果,可利用《几何画板》边实验边观察边分析,大胆地猜测结果,并制作成一个2至3分钟的小课件.
问题1设椭圆离心率为e,长半轴长、短半轴长、半焦距分别为a,b,c,则e从0经过变化到1时,a,b,c之间有怎样的大小关系?a与b又有怎样的大小关系?
问题2设A,B是焦点在x轴上的椭圆长轴和短轴的一个端点,F1和F2是两焦点,PF2⊥x轴,则离心率e从0经过变化到1时,∠BAO与∠POF2大小关系如何?
问题3以F1F2为直径的圆为⊙O,则离心率e从0经过变化到1时,椭圆与⊙O有几个公共点?
问题4设椭圆离心率为e,以OA(A为长轴的一个端点)为直径的圆为⊙O,则离心率e从0经过变化到1时,椭圆与⊙O有几个公共点?
设计意图:利用奥苏贝尔“先行组织原理”组织教学,通过课前预习教学内容,让学生初步尝试观察与猜想的过程,鼓励学生有效运用教学媒体,实现的知识主动建构,提高创新能力和动手操作能力,在进行探究的过程中培养学生的创新意识和良好的个性品质,提高学习效率,学会了合作、学会了探究.预期效果是学生初步解答4个问题或初步掌握解题方向.
第二阶段:创设情境——研讨交流
教师首先演示随离心率e变化的一般圆锥曲线动态图,让学生感知当离心率e从0向+∞逐渐变化时,动点轨迹随着从圆到椭圆到抛物线再到双曲线的变化过程,既看到了量变引起质变,有限跨向无限的生动历程,又领略了离心率的奇妙功能,在此基础上点明本节课的研究课题.其次让学生交流预习结果,教师视学生交流情况组织教学,必要时灵活选择以下方法给予支撑.
学生极易发现结论1:
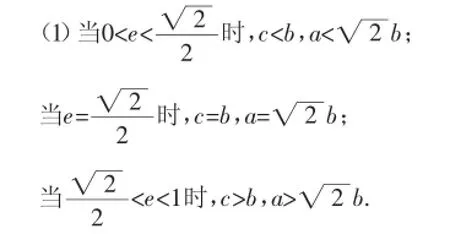

图1

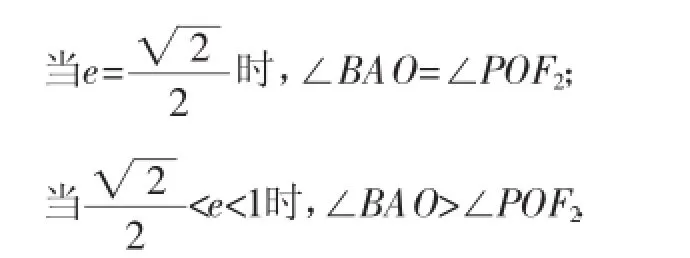
学生不难猜想出结论3:

学生能够猜想出结论4:
验证的方法仍是解方程组法.
设计意图:进一步让学生感悟某些特殊圆与椭圆的内在关系,为后续探究作好铺垫.第二阶段整个设计是个生成性设计,主要为学生创设了研讨交流的平台.引导学生利用现代教育技术手段自行获取有关知识,鼓励学生大胆地用直觉去寻找解决问题策略.预期效果是学生顺利完成4个问题解答.
第三阶段:深入探究——解决问题
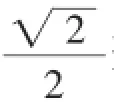
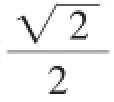
验证方法同上,只不过要注意到,由PA⊥PB知,OAPB是正方形,|PO|=
设计意图:其一是让学生能自主发现类似于上述的结论,其二是通过深入的观察、分析,培养学生猜想验证能力及联想挖掘能力,不断地渗透分类讨论的思想.在此过程中学生可能出现困难,必要时教师可从观念和方法的高度激活学生的思维,帮助学生选择解决问题的思维策略和模式,寻找问题解决的入口处,整个探究过程教师应及时调控,验证要详略得当,必要时可留给学生课外练习.预期效果是学生在教师的引导下顺利解答问题5、6.
第四阶段:联想变形——扩大战果


本教学设计使用多媒体课件,引导学生参与数学探究,是学科内研究性教学的一次有益尝试,学生在探究的过程中,不仅学到数学知识以及蕴涵其中的数学思想方法,更重要的是体验了数学知识的内在联系和内在美,领悟了数学探究的基本方法.
1.罗东荣.椭圆与离心率相关的几类最值[J].数学通讯,2012,10.
2.屠新民.关于曲线的离心率[J].数学通讯,2014,3.
3.易文峰.例说椭圆离心率的背景探求.[J]数学教学研究,2013,5.
