例谈“绝对值三角不等式”的研究与拓展
2017-04-21江苏省泰兴市第二高级中学毛玉峰
☉江苏省泰兴市第二高级中学 毛玉峰
例谈“绝对值三角不等式”的研究与拓展
☉江苏省泰兴市第二高级中学 毛玉峰
绝对值三角不等式是人教版选修4-5中的重要内容之一,它是求解含有多个绝对值符号的函数最值问题最有力的解题工具.在近几年的高考与竞赛中,含有多个绝对值符号的函数最值问题已是屡见不鲜.学生遇到这样的问题,往往都是通过分类讨论,分段求最值来处理,运算繁杂且很容易出错.“绝对值三角不等式”中蕴含了拆项、添项、配凑等数学方法,如果考生能够熟练掌握、灵活应用,在解题时就能达到事半功倍的效果,下面举例来进行说明.
一、定理展示
定理:如果a,b都是实数,那么|a+b|≤|a|+|b|,当且仅当ab≥0时,等号成立.
把定理中的实数换成向量a,b,结论依旧成立,它的几何意义是三角形两边之和大于第三边,等号成立的条件是a,b同向.由于定理与三角形之间的这种联系,我们称其中的不等式为绝对值三角不等式.
二、推广拓展
在处理具体问题时,仅靠上述定理是远远不够的,多数情况要用它的推广拓展:
结论1:∀a,b∈R,则|a|-|b|≤|a+b|≤|a|+|b|.(右边“=”成立⇔ab≥0,左边“=”成立⇔(a+b)b≤0)
结论2:∀a,b∈R,则|a|-|b|≤|a-b|≤|a|+|b|.(右边“=”成立⇔ab≤0,左边“=”成立⇔(a-b)b≥0)
结论3:∀a,b∈R,则||a|-|b||≤|a+b|≤|a|+|b|.(右边“=”成立⇔ab≥0,左边“=”成立⇔ab≤0)
结论4:∀a,b∈R,则||a|-|b||≤|a-b|≤|a|+|b|.(右边“=”成立⇔ab≤0,左边“=”成立⇔ab≥0)
结论5:(1)设x1≤x2≤…≤x2m,m∈N*,则当x∈(xm,xm+)1时|x-xi|取得最小值;

结论6:设x1≤x2≤…≤xn,n∈N*且n>1,则
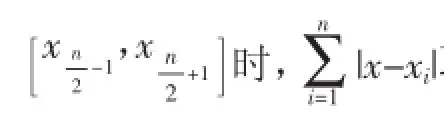
结论7:(1)设x1<x2,m,n∈N*且n≥m,则当x=x1时,n|x-x1|+m|x-x2|取得最小值;
(2)设x1<x2,m,n∈N*且n≤m,则当x=x2时,n|x-x1|+ m|x-x2|取得最小值.
三、研究与应用
(一)求最值或证明题
例1已知函数f(x)=x2+ax+b(a,b∈R),记M(a,b)是|f(x)|在区间[-1,1]上的最大值.
(1)证明:当|a|≥2时,M(a,b)≥2;
(2)当a,b满足M(a,b)≥2,求|a|+|b|的最大值.
此题是浙江的一道高考压轴题,方法很多,此处以绝对值三角不等式解决,以显其威力之大.

所以M(a,b)=max{|f(-1)|,|f(1)|}.
(1)从绝对值本身入手,在含绝对值问题的本身、本质、几何意义等处下工夫.
证法1:利用|x|≤a⇔-a≤x≤a(a>0)去绝对值,
因为M(a,b)=max{|f(-1)|,|f(1)|},
所以M(a,b)≥|f(1)|=|1+a+b|,
M(a,b)≥|f(-1)|=|1-a+b|,

两式相加得-2M(a,b)≤2a≤2M(a,b),
故M(a,b)≥|a|≥2.
证法2:利用绝对值三角不等式|a|+|b|≥|a±b|进行放缩解决问题.
因为M(a,b)=max{|f(-1)|,|f(1)|}
=max{|1-a+b|,|1+a+b|}

所以当|a|≥2时,M(a,b)≥2.
(2)从(1)的方法中可选择“从绝对值本身入手,在含绝对值问题的本身、本质、几何意义等处下工夫”.
方法1:从绝对值三角不等式|a|+|b|≥|a±b|入手,进行巧解.

所以|a|+|b|max=3,当a=±2,b=-1时取等号.
方法2:因为M(a,b)≤2,又M(a,b)=max{|f(-1)|,|f(1)|}=max{|1-a+b|,|1+a+b|}≤2,

故M(a,b)=|1+b|+|a|≤2.
因为|1+b|+|a|≥|b|+|a|-1,所以|b|+|a|≤3.
所以|a|+|b|max=3,经检验当a=2,b=-1时能取到等号.
≥|x-1|+|x-19|+|x-2|+|x-18|+…+|x-9|+|x-11|+|x-10|
≥|(x-1)-(x-19)|+|(x-2)-(x-18)|+…+|(x-9)-(x-11)|+|x-10|
≥18+16+…+2+0=90,
当且仅当(x-1)(x-19)≤0且(x-2)(x-18)≤0且…且(x-9)(x-11)≤0且x=10,即x=10时,等号成立.
故f(x)的最小值为90.
(二)存在性问题
例3关于x的不等式|a|≥|x+1|+|x-2|,若存在实数解,则实数a的取值范围是________.
解:只需(|x+1|+|x-2|)min≤|a|即可,利用结论可知,
3=|(x+1)-(x-2)|≤|x+1|+|x-2|.
由|a|≥3,解得a∈(-∞,-3]∪[3,+∞).
(三)恒成立问题
解:依2|x|+|x-2|+2|x-1|>2m恒成立,
可令y=2|x|+2|x-1|+|x-2|=|x|+|x|+|x-1|+|x-1|+|x-2|,
min

(四)求方程根的个数等问题
(五)解决不等式问题
例7解不等式:|2x+1|-|x-2|<|x+3|.
解:原不等式等价于|2x+1|<|x-2|+|x+3|,又因为2x+ 1=(x-2)+(x+3),
所以|(x-2)+(x+3)|<|x-2|+|x+3|,即(x-2)(x+3)<0.
所以原不等式解集为{x|-3<x<2}.
(六)已知最值求参数的值
例8若函数f(x)=|x+1|+|2x+a|的最小值为3,则实数a的值为_________.

例9已知a>0,b>0,c>0,函数f(x)=|x+a|+|x-b|+c的最小值为4,求a+b+c的值.
解析:f(x)=|x+a|+|x-b|+c≥|(x+a)-(x-b)|+c=|a+b|+ c,当且仅当-a≤x≤b时,等号成立
又a>0,b>0,所以|a+b|=a+b,所以f(x)的最小值为a+ b+c,所以a+b+c=4.
总之,高考数学命题遵循考试大纲和课标,体现“基础知识全面考,主干内容重点考,热点知识反复考,冷门知识有时考”的命题原则.从解答策略上来说,高考一般淡化解题中的特殊技巧,比较注重在解题的通性通法上精心设计.但是认真分析近几年的高考试题,我们不难发现,由很多难点问题既可以用“通性通法”解决,但同时有的时候却不行.因此,在平时学习中,有必要适当掌握更多的方法和技巧,只有这样,才能真正在高考中做到处变不惊,游刃有余.绝对值三角不等式是一个重要的不等式,对于含有绝对值的函数求最值问题,应优先考虑此不等式,当然有时候需要适当变形,同时要特别注意等号成立的条件.
