从一道解几试题谈数感培养
2017-04-21江苏省梁丰高级中学
☉江苏省梁丰高级中学 樊 亚
从一道解几试题谈数感培养
☉江苏省梁丰高级中学 樊 亚
一、给出问题
分析:本题考查的是直线和椭圆位置关系,对于求解面积可从三种不同的直线方程入手,但是计算量有不小区别,我们先来看看解答.

(2)当直线AB的斜率存在时,由题意可设直线AB∶y=k(x-1),O到AB的距离为d,A(x1,y1),B(x2,y2).

解法2:由题意可知,斜率为0的直线无法构成三角形,故可设直线AB:x=my+1.


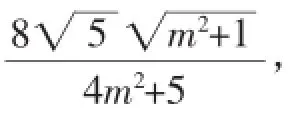
二、寻根究底
1.预算——简化计算的法宝

思考1:那么对于问题中的解法1和解法2,解题思路是一样的,都是利用S△OAB=|AB·|d公式进行计算的,只是所设直线方程的形式不同,解法1设为y=k(x-1),解法2设为x=my+1,那么计算繁简程度为何有所不同?
思考2:既然设的方式不同会影响计算繁简程度,那么做题前如何选定所设直线的形式呢?
分析:由思考1的分析可知,面积公式的繁简程度问题主要在于O到直线AB的距离,因此我们可以在做题之前先对两种情况分别预算,那么就可以大致看出哪种形式的直线方程更便于计算.例如:

(2)若直线设为x=my+1,则S△OAB=|AB|·d=·
显然第二种方法三角形面积公式分子最高次数相对较低,而我们在计算之前如果能掌握这种预算的方法,那么就会大大加快计算的速度及准确率,因此预算能降低圆锥曲线的计算难度,是解圆锥曲线中不可缺少式的,但是解法1:O到直线AB的距离的方法之一.
2“.动”中找“定”简化计算
对于定点直线系三角形面积的求解中,可以利用直线的“定”的因素,简化计算过程.例如问题的解法3,将面积划分为几个三角形的面积之和(差),而这些小三角形是同底或等高的,因而面积则可变为高之和(差)或底之和(差)的形式.
3.实例验证
思考3:问题中的定点是在x轴上,那么若将定点改为y轴,以上方法是否也可行?
为解决这一问题,笔者将题改为:

解法1:用S△OAB=|AB·|d计算.
分析:用预算法,可以确定将直线设为y=kx+3计算相对简单.然而设直线时无论用哪种形式都需要考虑特殊情况,即斜率不存在或者是平行于x轴的情况,即要分类讨论.

解法2:S△OAB=S△OPB-S△OPA=|OP(||x2|-|x1|),由于A、B必在y轴同侧,因此S△OAB=|OP·||x2-x1|=|x2-x1|.
分析:在动直线中找定量,能简化计算,提高效率,因此我们可以在解题过程中培养动中找定的思维方式,以提高解题的效率与成功率.
三、解题思考
在研究这个题组的过程中,笔者紧紧围绕学生出现的困惑及难点分析和反思,在寻找解决方法的过程中,不仅解决学生解题中遗留下来的困难,同时分析困难的归因、解决的方法以及是否可以通过其他方式避免或替代这些困难,从而达到简化、优化算法提高解题效率的目的.这就需要教师具有以下几个要求:
1.教师要善于发现问题
学生的习题错误是一个非常好的资源来源处,作为教师批改作业不仅仅要检测学生的掌握程度,更要从中挖掘学生错误的缘由,从学生的角度去思考问题,这样教师才能真正意义上了解学生对知识点的掌握情况.学生的错误常见为:计算错误、题意理解错误、知识没掌握引起的错误、过程舍近求远造成计算复杂化而无法求解等情况.教师要对学生出现错误原因进行分类,将错误作业根据错误人数以及错误原因分为课堂讲评型和个别讲评型,根据不同的错误原因,对症下药,这样才能达到事半功倍的效果.因此,本题组从学生错误的原因可归为过程复杂化导致增加计算难度的类型.针对这一困难,笔者采取的方法是:第一,将计算进行到底,让学生明白自己的解法也是正确的,但是需要较高的计算能力;第二,通过对不同解法的分析比较,教导学生寻找简化、优化的算法,以提高学生解题的效率和正确率.
2.教师要善于刨根问底
教学不仅仅要将知识点的来龙去脉讲清楚,更重要的是要了解学生对知识的理解程度,因此教师要善于对知识刨根问底.首先,教师要具备对教材进行刨根问底式的反思技能.随着课改的不断更新,教师要时刻关注教学内容以及教学范围、知识的教学深度等,在把握住重难点的同时,要时刻反思所教内容的教学功能,这样才能从根本上传递教材想要培养的学生的数学思想和能力.其次,教师要具备对学生知识的掌握情况进行刨根问底式的反思技能.教师要弄清以下几方面:(1)学生错误的原因是什么;(2)错误是属于知识性错误还是技能性错误;(3)如何能避免这些错误;(4)为什么改善后的解题方式可以避免错误.反思这些问题,就能让学生明白错误的缘由,从理解的层面上纠正错误.同时刨根问底式的反思也能反过来促进教师的教学技能,在不断地自问自答过程中,剖析教材、剖析错误,以揭示知识的本质,为教学指明方向.
3.教师要善于培养学生的“数感”
“数感”如同“语感”,不是一朝一夕就能练就的,需要老师在教学过程中不断培养.“数感”是学生通过数学活动得到感受和体验而积累下来的数学经验.“数感”能力的强弱直接影响学生解题思路的开阔程度和解题能力的高低程度,因此培养学生的“数感”至关重要,如何培养学生的“数感”就成为教师研究探讨的重要方向.
第一,运用类比培养“数感”.
通过类比可以达到知识、解题技巧、学习方法的迁移,使新知能在既熟悉又陌生的环境中被学生理解和接受.在类比的过程中,学生掌握类比的方法,这就是“数感”培养的方法之一.例如平面向量与空间向量的类比,等差数列与等比数列的类比,平面几何与立体几何的类比等等,通过类比较大程度地降低了对新知的理解难度,加快了对新知的接受速度,实现了提高效率的教学目标.
第二,运用联想培养“数感”.
所谓联想就是寻找新事物与旧事物相类似或有关联之处,通过联想、对比、区别等方式,运用转化与化归的方法找到解决途径.联想可以是知识之间关系的联想,可以是解题方法的联想,也可以是学习手段的联想等等,联想能够帮助转化与化归思想落到实处.例如:已知定点A(2,1),F(1,0)是椭圆=1的一个焦点,P是椭圆上一点,求|PA|+|PF|的最值.
分析:学生第一次做这题时是毫无头绪的,因此笔者把椭圆联想成直线,即问题可改为:在直线l上找一点P,求点P到定点F、A的距离之和(差)的最值.
我们已学过,当两定点在直线异侧时,可以通过对称来求|PA|+|PF|的最小值;当两定点在直线同侧时,可以求|PA|-|PF|的最大值.但此题是椭圆,因此较难实现对称,因此A、F同时在椭圆内部可以联想成A、F在直线同侧,因此可以求差的最大值,这就易于想到用椭圆定义,即|PF|+|PF′|=2a,将|PA|+|PF|转化为求2a+|PA|-|PF′|的最值问题,从而得出P、A、F′三点共线时2a+|PA|-|PF′|就有最值.这样的联想自然,而且能让学生豁然开朗,解决了“直接灌输给学生利用椭圆定义化归为求2a+|PA|-|PF′|最值问题”的生硬和牵强,也让学生体会联想的奇妙之处,从而实现“数感”的培养.
1.黄严生,束从武.例谈“问思”教学法[J].中学数学教学,2013(1).
2.周立志.巧用课堂教学中的典型错误提升课堂效率的若干策略[J].中学数学教研,2013(4).
3.殷伟康.数学课堂教学中追问的特征与时机[J].数学教学研究,2013(1).
