本是同根生,如此奇异争
——2016年高考北京卷两道解析几何试题的探究与思考
2017-04-21甘肃天水市一中宫前长
☉甘肃天水市一中 宫前长
本是同根生,如此奇异争
——2016年高考北京卷两道解析几何试题的探究与思考
☉甘肃天水市一中 宫前长
一、例题呈现
(1)求椭圆C的方程;
(2)设P是椭圆C上一点,直线PA与y轴交于点M,直线PB与x轴交于点N,求证:|AN|·|BM|为定值.
(1)求椭圆C的方程及离心率;
(2)设P为第三象限内一点且在椭圆C上,直线PA与y轴交于点M,直线PB与x轴交于点N,求证:四边形ABNM的面积为定值.
二、试题特征剖析
上述文、理试题的设置背景都是基于一个椭圆(根),只是给出椭圆的标准方程的求解方式不同而已,最终所得的椭圆方程都是+y2=1,命题老师主要考虑到文、理学生的学习层次和理解程度的差异,命制不同方式,让每一位学生都能够求出椭圆的标准方程;文、理题目均设置具有递进结构的两个小问,力求注重基础,稳中求变,通过第(2)问的细节来控制试题的难度,完全符合新课标的要求和数学教学理念,是北京卷中难度较大的一道好题.
例题1、2的条件给出的椭圆的标准方程结构表明在焦点在x轴上,如何求其方程呢?例题1的第(1)问需要借助离心率和三角形的面积公式,利用方程组求得椭圆的标准方程,但例题2是给出椭圆的两个顶点坐标,可以直接写出椭圆的标准方程和离心率,比起例题1的第(1)问简单多了,属于送分小题,也符合文科学生学习解析几何的心理要求.
接着观察第(2)问,发现意味深长的命题特征:理科“P是椭圆C上一点”表征“点P的任意性”,而文科“P为第三象限内一点且在椭圆C上”表征“点P的确定性”,第(2)问考查相同方向下不同的是“目的地”:例题1是证明“|AN|·|BM|为定值”,例题2是证明“四边形ABNM的面积为定值”(一个是线段积为定值,一个是面积为定值).
从所需“证明”的表征上看,证明“|AN|·|BM|为定值”属于特殊线段(非弦长)的积,运算繁,难度较大;而证明“四边形ABNM的面积为定值”属于通过计算四边形的面积说明定值,学生容易想到“对角线互相垂直的四边形的面积等于对角线乘积的一半”进行解题,入手宽,难度适中,文科学生容易接受和理解.因此,命题人考虑到了文、理科学生的学习特征和学习能力,也让每一位学生从心理上消除了对解析几何中“定值”问题的顾虑,让每一位学生的解题能力都得到了充分的发挥,有效地落实了新课标的理念.
三、解法探究
(一)例题1解法探究
1.思路


2.解题时要明确“目标”
根据已知条件分别求出|AN|,|BM|的值,求其乘积为定值.采用“设而不求”的策略解题时,一定要注意条件中的“点P”具有“任意性”(点P不确定),往往会引起相应的分类讨论.因此,对点P的坐标采用“设而不求”的策略,具体设置方法有两种:代数式坐标P(x0,y0)和参数式坐标P(2cosθ,sinθ).
思路1(直接求解的视角):先设出椭圆上的一点P的坐标(x0,y0),再根据直线与坐标轴相交,求得交点坐标,利用两点间的距离公式求得|BM|,|AN|的值,进而求得|AN|·|BM|的积是一个与x0,y0无关的常数.
解法1:由(1)可知,A(2,0),B(0,1),设P(x0,y0),则x2
0+4y2
0=4.
当x0≠0时,直线PA的方程:y=y0
x0-2(x-2).令x=0,计算得yM=-2y0x0-2,从而|BM|=|1-yM|=1--2y0x0-2
()=1+2y0
x0-2
.直线PB的方程:y=y0-1 x x+1.令y=0,计算得xN=-x0y0-
0 1,从而|AN|=|2-xN|=2+x0y0-1
.因此,|AN|·|BM|=1+2y0x0-2 ·2+x0
y0-1
=x2
0+4y20+4x0y0-4x0-8y0+4 x0y0-x0-2y0+2 =4.
当x0=0时,y0=-1,|BM|=2,|AN|=2,则|AN|·|BM|=4.
综上所述,|AN|·|BM|为定值.
点评:解法1的关键是发现x0,y0的关系,通过化简|AN|·|BM|(含x0,y0)的代数式,得到一个与x0,y0无关的常数即可得证,还要注意对特殊位置(x0=0)这一情况的处理.
思路2(参数方程的视角):利用椭圆的参数方程,即可设出椭圆上的一点P的坐标为(2cosθ,sinθ),再想办法求得|BM|,|AN|的值,进而求得|AN|·|BM|的值是一个与θ无关的常数.由于参数θ的任意性,解题时不像解法1进行分类讨论了
解法2:由(1)可知,A(2,0),B(0,1),设P(2cosθ,sinθ),
直线PA的方程:y=sinθ 2cosθ-=4x0y0-4x0-8y0+8
x0y0-x0-2y0+2 θ,从而可得点M的坐标0,sinθ
1-cosθ 2(x-2).令x=0,计算得yM=sinθ 1-cos
().
故|BM|=|1-yM|=1-sinθ 1-cosθ
.直线PB的方程:y=sinθ-1 2cos θx+1.令y=0,计算得xN=2cosθ 1-sin
()θ,从而可得点N的坐标2cosθ 1-sinθ,
0.故|AN|=|2-xN|=2-2cosθ 1-sinθ
.因此,|AN|·|BM|=1-sinθ 1-cosθ ·2-2cosθ
1-sinθ =2(1-sinθ-cosθ)2
(1-sinθ)(1-cosθ
)
.
又因为(1-sinθ-cosθ)2=2(1-sinθ-cosθ+sinθcosθ)= 2(1-sinθ)(1-cosθ),可得|AN|·|BM|=4.
故|AN|·|BM|为定值.
点评:解法2将点P的坐标设为参数形式,解题策略仍是采用点P的坐标“设而不求”,其他的思路、方法与解法1一样不变,同样可以算出|AN|·|BM|的值为定值.
思路3(利用仿射变换的视角)利用椭圆与圆的仿射关系(人教A版),将椭圆问题转化为圆的相关问题,这也是解决椭圆问题的基本方法.对于此题,只需要通过椭圆的仿射变换,证明圆中相应的线段之积是一个常数即可说明:|AN|·|BM|为定值.
解法3:根据(1)的椭圆方程:x24+y2=1,变形为x2+ 4y2=4可知通过仿射变换为x′=x,y′=2y{,椭圆转化为圆:x′2+ y′2=4.也就是说:将椭圆x2
y
B0
2|B0M0|=2,
在圆中,可得∠B0MA=∠P0B0M0+∠B0P0A=∠P0B0M0+∠AB0M0=∠P0B0A,且∠NAB0=∠AB0M0,
所以△ANB0∽△AB0M0,所以|AN|
|AB04+y2=1上的所有点的横坐标不变,纵坐标伸长到原来的两倍,得到圆x′2+y′2=4,此时圆心就是椭圆的中心,椭圆上的点P对应圆上的点P0,圆与x轴的交点恰好就是椭圆的左右顶点,圆与y轴的交点B0,M0分别对应椭圆中的点B,M.
根据圆的对称性和仿射
变换的性质,可得|OM0|=2|OM|=
2,|BM|=1
N
B
A
O
x
PM
P0
M0
图1 |,从而|AN|·|B0M0|=|AB0|2=8,
故|AN|·|BM|=4,即|AN|·|BM|为定值.
思路4(斜率、向量的视角)根据三点共线,转化为斜率相等或向量共线来进一步证明|AN|·|BM|为定值. |=|AB0| |B0M0

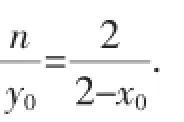
化简得[mn-(m+2n)]2=4,
即mn-(m+2n)=2或mn-(m+2n)=-2.
又因为|AN|·|BM|=|2-m|·|1-n|=|2+mn-(m+2n)|=4或|AN|·|BM|=0(舍去),
故|AN|·|BM|为定值.
(二)例题2的解法探究
第(1)问从条件可得a=2,b=1,很容易地得到椭圆的标准方程下面主要对第(2)问的解法探究:题设所涉及的四边形的对角线恰好垂直,根据“对角线互相垂直的四边形的面积等于对角线乘积的一半”可得四边形的面积就是例题1第(2)结论的“一半”,即S四边形ABNM=|AN||BM|=2.从这一点上看,例题1、2明显地露出了“一根(椭圆)两支花(线段之积,面积为定值)”,命题人巧妙地设置“证明”;分离两个“目标”:“|AN·||BM|为定值”、“四边形ABNM的面积为定值”.
对四边形ABNM的面积的计算,可用上述方法求得(如解法1);从其他视角进行探究:利用等面积法求得|AN|和|MB|的值(解法2)或利用“等价转化”的方式计算所求四边形的面积(如解法3).
思路1(参数方程的视角):根据椭圆的参数方程,设出点P的坐标(2cosθ,sinθ),再计算出|AN|和|BM|的长度,根据“对角线互相垂直的四边形的面积就是对角线乘积的一半”可求得四边形ABNM的面积.
解法1:因为A(2,0),B(0,1),根据(1)知,可设P(2cosθ,sinθ).
四边形ABNM的对角线互相垂直,所以四边形ABNM的面积:
又因为(1-sinθ-cosθ)2=2(1-sinθ-cosθ+sinθcosθ)= 2(1-sinθ)(1-cosθ),可得SABNM=2.
故四边形ABNM的面积是2.
解法2:根据题意可求得直线AB的方程:x+2y-2=0,由(1)可知,设P(2cosθ,sinθ),
所以三角形PAB的面积:

其中|dP-AN+dB-AN|=|1-sinθ|,|dA-BM+dP-BM|=2|1-cosθ|,
下面依据解法1可以求得故四边形ABNM的面积:SABNM=2.
思路3(等价转化的视角):要证明四边形ABNM的面积是定值,从图形结构教育猜想,四边形ABNM的面积可能与三角形A1AB的面积一样,只需证明即可.
解法3:根据题意,证明四边形ABNM的面积与△A1AB的面积相等,也就是证明△A1BN与△ANM的面积相等.
+ y2=1,其左顶点A(1-2,0),直线PB的斜率k是存在的,且k>0,则直线PB的方程:y=kx+1(k>0),
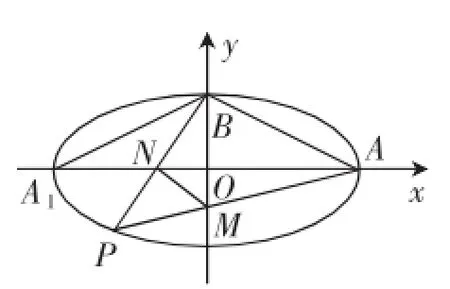
图2

容易求得点P的横、纵坐标,

再由直线PB的方程:y=kx+1(k>0),解得点N的横坐标:xN=-

从而有S△A1BN=S△ANM,说明三角形A1BN的面积与三角形ANM的面积相等,即四边形ABNM的面积与三角形A1AB的面积相等,因此,
ABNM△A1AB值).
四、一般化探究
根据两道例题的特征剖析和解法探究,进行一般化处理,可得下面的问题:
试问:(1)|AN|·|BM|为定值?
(2)若点P为第三象限内一点且在椭圆C上,四边形ABNM的面积为定值?

由于P是椭圆C上一点,对点P的位置进行分类:
当x0=0时,y0=-b,此时|BM|=2b,|AN|=a,所以|AN|· |BM|=2ab(定值).显然|AN|·|BM|为定值,四边形ABNM的面积:S=ab(定值).




(2)因为点P为第三象限内一点且在椭圆C上,根据“对角线互相垂直的四边形的面积等于对角线乘积的一半”,可得S四边形ABNM=|AN||BM|=ab(定值).
综上所述,|AN·||BM|为定值2ab,并且四边形ABNM的面积为定值ab.
此时可知,点P在椭圆的其他位置时,四边形ABNM不一定是凸四边形,情况比较复杂,需要分类讨论.
五、反思
1.重视思辨,多维设想
对于高考题,一定要多联系、多思考,寻找问题间的共性和差异,建立完整的数学概念体系,才能够厘清数学题中概念与其他数学知识之间的联系,才有可能做到整体把握、准确定位.2016年北京卷的两道解析几何试题,放在一起研究,通过思辨,就会暴露出很清晰的命题思路、考查的目标要求,试题虽然“寻常”,但其教学“导向”韵味深长.
2.目标引领,重点突破
例题1、2突出考查了学生分析和解决问题、推理论证的能力,在考查数学思想方法的同时,关注数学各部分内容的知识与相互关联,引领教师在教与学的过程中,多关注思想方法、强调能力立意,加深对数学的认识和本质的理解,起到了正导向的作用.
对于解决定值、定点问题,从问题的整体上把握、应用解题策略.如解决定值、定点问题的方法:(1)从特殊入手,求出定点、定值、定线,再证明定点、定值、定线与变量无关;(2)直接计算、推理,并在计算、推理的过程中消去变量,从而得到定点、定值、定线.解题过程中,一定要注意到“繁”“难”的代数运算是此类问题的特点,设而不求方法、整体思想和消元的思想的运用可有效地简化运算.唯有如此,方可突破难点——定值、定点问题.
总之,在平时解题训练的过程中,学生要多思考题目条件和所问之间的联系,从设问方法入手多总结,才能在解题的过程中不断提升,即使难度增加,解题时也会得心应手.
