试卷讲评课的教学思考

☉福建省厦门市海沧中学 谢永广

试卷讲评课的教学思考

☉福建省厦门市海沧中学 谢永广

考试是对学生阶段性所学知识的掌握程度的检验、对试卷的讲评，不仅可以检查学生对所学知识的结构的掌握是否完善，分析问题、解决问题、计算能力是否过关，也能发现教师本身在教学中的不足之处，进行自我总结反思，不断改进教学策略.但在讲评过程中，我们易陷入以下几个误区.

1.讲评不及时，使讲评课堂的效果不理想

现在数学教师的教学任务非常重，既要赶教学进度、新课作业错误纠正，还要抽时间辅导学生，往往把考过的试卷放在一边或过好几天再讲评，到学生把做过的试题忘得差不多了再去讲解，这样讲解的效果就会大打折扣.

2.一讲到底，学生主体参与不够

很多老师到讲解课时，拿了试卷就进教室，选择题、填空题报一下答案就算完，根本不让学生参与，这与给学生一张正确答案的试卷没有什么区别.

3.讲评没有针对性，减弱了试卷讲评的效果

有些教师在讲评课前既不作正确的统计，也不作错误原因根源的分析，如何找到正确的途径？试卷讲评时，往往按部就班，顺次讲解，眉毛胡子一把抓，学生没搞清的问题一掠而过，不需要多讲的地方却花一样多的时间，使得学生在讲评课时机械地记答案，没有激情，一节课下来，收益甚微，事半功倍.

4.忽视方法指导与思维训练

有些试卷讲评课，老师将正确的答案或解法告诉学生，而没有告知学生应如何从哪几方面进行解题思路的分析？用什么样的思维去思考，缺乏指导，更谈不上挖掘试题功能进行思维训练.

5.忽视不同层次学生的不同需求，浪费部分学生的时间

有的老师讲评试卷，要么基础题目反复讲，综合题告诉学生一种解法；要么基础题一掠而过，较难综合题讲一节课，使大部分学生收获甚少.这样浪费了学生的学习时间也挫伤了学习的积极性，使很多学生厌倦试卷讲评课.

那么如何讲评才能取得良好的效果呢？笔者提出以下几点建议供参考.

一、追本求源，促使学生深入掌握基础知识

例1（2015高考山东卷理）一条光线从点（-2，-3）射出，经y轴反射与圆（x+3）2+（y-2）2=1相切，则反射光线所在的直线的斜率为（）.

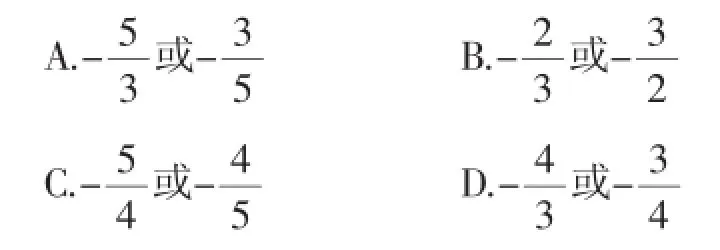
评析：本题体现了直线与圆的位置关系的应用.开始时觉得解题无从着手，说明对物理中的“光学原理”和点关于直线对称的知识理解不够.本题首先可得到（-2，-3）关于y轴对称点的坐标为（2，-3），设出反射光线所在直线的方程y+3=k（x-2），由反射光线与圆（x+3）2+（y-2）2= 1相切，利用圆心到反射光线所在的直线的距离等于圆的半径求解.本题重点考查解析几何中的对称和直线与圆的位置关系等知识，将考查目的详细分析后，能使学生深入掌握基础知识

二、原题变式，促进学生对知识点本质的掌握

围绕某个知识点进行“变式训练”，通过多层次、多方位、多角度对数学问题进行探究与思考，可帮助学生打通思维的关节，在头脑中构建新知，展现数学知识的发现、发生和发展的过程，有目的有意识地启发引导学生积极从“变”的现象中发现“不变”的本质，从“不变”的本质中探寻“变”的规律，使已有的知识与所学的新知识在头脑中融会贯通.

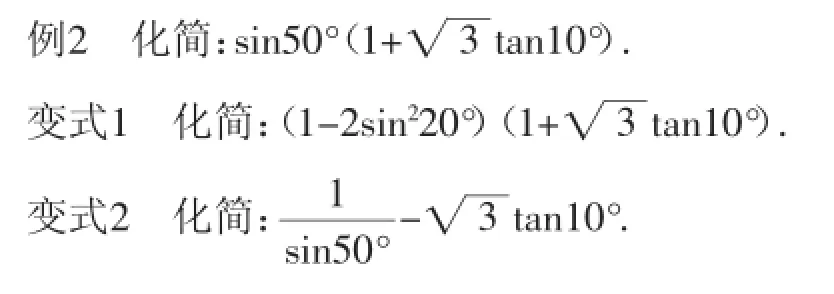
评析：通过以上的变式，学生可以对三角恒等变换的基本思路是：“一角二名三结构”（角的变换主要涉及倍半、互补、互余之间的转换；函数名之间变换主要涉及切化弦和正、余弦之间的转换；结构的变换主要体现在公式的逆用、变形用）的理解更加深入，而且变式增强学生灵活运用知识的能力.

三、一题多解，优化学生的解题思维

试卷讲评不仅是对学生解法的纠偏纠错过程，也是汇总学生优秀解法，分享学生好作品的契机.在分享的过程中，优秀解法能充分调动学生学习的积极性.在交流的过程中，重新点燃了思维的火花，从旧知得到新知，丰富了解法，进一步拓展了学生的能力.针对某一题目，若从不同的视角寻找问题的切入点，常可得到多种解题方法.教学中教师要善于引导学生打破常规思维，暴露最原始的想法，敢于把对问题最直接的认识呈现出来.通过学生之间的交流，取长补短，从而实现对问题的最优解答.

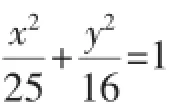
A.P点有两个B.P点有四个

C.P点不一定存在D.P点一定不存在

这是一道考查椭圆的几何性质应用的试题.在讲评时我让学生自己来讲解解题思路，以暴露学生思维过程，共得到以下八种不同的方法.

学生1：设圆的方程为x2+y2=9，椭圆的方程为=1，两者联立解方程组无解.故圆x2+y2=9与椭圆1无交点，即PF1不可能垂直PF2.

学生2：以F1F2为直径构圆，圆的半径r=c=3＜4=b，即圆与椭圆不可能有交点.

学生3：设P（5cosθ，4sinθ），由PF1⊥PF2知而=（5cosθ+3，4sinθ）（5cosθ-3，4sinθ）=25cos2θ-9+ 16sin2θ=0⇒cos2θ=-（舍去）.故选D.

学生4：由题意知，（S△PF1F）2max=·|F1F2|·b=3×4=12，而在椭圆中，S△PF1F2=b2tan

学生5：由题意知，当P点在短轴端点处∠F1PF2最大，设∠F1PF2=2α，tanα=＜1⇒α＜，此时∠F1PF2为锐角，与题设矛盾.故选D.

学生6：设∠PF1F2=θ，假设PF1⊥PF2，则|PF1|+|PF2|= 6cosθ+6sinθ=6，而|PF1|+|PF2|= 2a=10，即10≤6不可能.故选D.

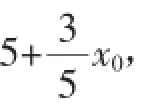
通过不同解法的比较、分析，使学生真正掌握此类问题的解法的同时，也拓展了学生的解题思维.

四、深化知识点，提升学生研究问题的能力

例4如图1，在圆锥SO中，已知底面半径r=1，母线长l=4，M为母线SA上的一个点，且SM=x，从点M拉一根绳子，围绕圆锥侧面转到点A.

（1）求绳子的最短长度的平方f（x）；

（2）求绳子的最短长度的最小值和最大值.

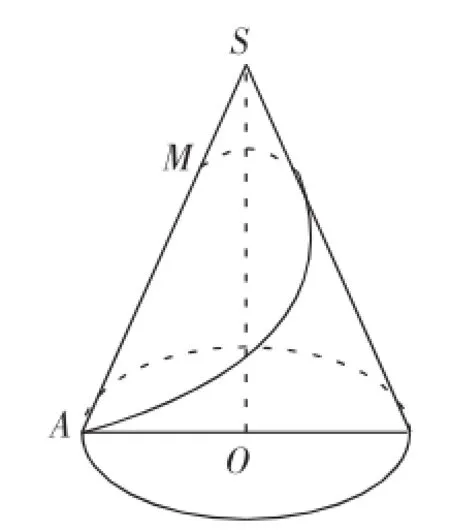
图1

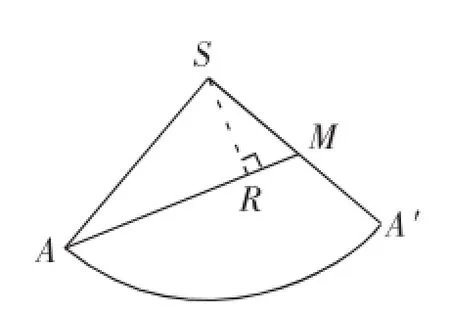
图2

思路探索：

①题目给出的是已知底面半径、母线长的圆锥，需要求的是圆锥侧面上两点A、M间所拉绳子的最短长度（两点间的最短距离），如何来求最短长度？在圆锥侧面上“绕来绕去”恐怕很难确定何时长度最短.如图2，沿母线SA将圆锥的侧面展开，“化曲为直”，连接AM即为绳子的最短长度.

②绳子的最短长度AM“找到”了，可如何用x表示它的平方呢？

由图2可以看出，只好“交给”△ASM了.

在△ASM中，已经知道SA=l=4，SM=x，那么，现在的关键就是去求侧面展开图——扇形的中心角∠ASA′了.怎样求出∠ASA′？这可能是许多同学“为难”的地方.下面我们一起解决掉这一难点.

我们知道，扇形是圆的一部分，圆周角是360°，只要知道扇形占所在圆的“份额”，扇形的中心角就能够求出来了.

这里，扇形所在的圆以圆锥母线的长SA=l=4为半径，圆周长为C=2πl=8π；

扇形的弧长（即圆锥底面圆的周长）为l′=2πr=2π.

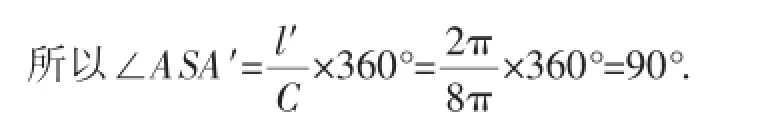
③求出∠ASA′=90°，在△ASM中利用勾股定理就可以用x表示出绳子的最短长度AM的平方f（x）.由于M为母线SA上的一个点，且SM=x，所以0≤x≤4.

④根据f（x）和x的范围，利用函数知识求出f（x）的最小值和最大值，进而求出绳子的最短长度的最小值和最大值.

通过上述的思路探索，请同学们完整地写出解题步骤.

这样讲解本题，既让学生感悟到知识的生成、发展过程，也训练了学生理解和掌握知识与技能.

五、站在高视角，分析命题动向

要想顺利解决某一问题必须紧扣题目的题设条件和待求结论.任何一道数学问题，都包含一定的数学条件和关系，要弄清核心条件是什么？待求结论与条件存在着何种依存关系.进而我们才能准确识别问题情境，确定解题路径，正确进行思维表达.

例5（2016全国卷Ⅱ理）已知函数（fx）（x∈R）满足（f-x）=2-（fx），若函数y=与y=（fx）图像的交点为（x，

1y1），（x2，y2），…，（xm，ym），则xi+y）i=（）.

A.0B.mC.2mD.4m

解析：本题关键条件有三个：①函数（fx）（x∈R）满足f（-x）=2-f（x）；②函数y=；③图像的交点为（x，

1y1），（x2，y2），…，（xm，ym），待求的是这m个交点横、纵坐标之和.不难发现，核心条件是“函数f（x）（x∈R）满足f（-x）=2-（fx）”，发现函数（fx）和函数y=都关于点（0，1），利用对称性求解.

综上，从教师的角度来看，要让学生在试卷讲评中有所收获，帮助学生提高数学思维品质.如何使试卷讲评走向实效，仍需广大同行在数学教学实践中不断总结.