基于卡尔曼滤波算法对电网频率进行检测和预测

,

(1.国网厦门供电公司，厦门　361000；2.国网泉州供电公司，福建　泉州　362000)

1　前言

随着现代电力电子设备和技术在电力系统中的广泛应用，将给电力系统传输、转换等带来频率扰动，导致电网安全、经济、可靠运行构成潜在威胁，同时也限制了电力电子设备和技术的发展速度[1]。因此，研究电力系统频率问题具有重要的工程应用价值[2]。电力电子装置属于新一代非线性负载，其引起的谐波会造成负载和输电设备的过载、失控和增加损耗，甚至严重危害电网和用电设备的安全[3]。此外，随着电力电子设备和技术逐步在工业、交通、国防等领域得到普遍的应用，电力电子设备研发技术不断提升，所具有的功率容量随之增加，电力系统运行时的频率波动也随之增大[4]。

为保证电力系统能够长期可靠安全运行，控制电力系统频率至关重要，而电力系统频率的正确检测又是控制电力系统频率的先决条件[5]。目前，国内外现有的电力系统频率检测主要有硬件检测和软件检测两大类，其中硬件检测主要采用过零比较器或锁相环实现，其具有不占用处理器时间等优点，但增加了硬件侦测电路的投入，成本较大且适用性不强，得到的频率值易受谐波和器件零点漂移干扰，不利于后续研究[6]。软件检测与硬件检测完全不同，其采用某种智能算法对采样信号进行分析，最终获取出频率信息。软件检测需占用检测系统处理器时间，但不要增加硬件电路投入，大大地降低了投入成本，且能将干扰信号滤除，检测结果更加可信。经过近几年科技的发展，国内外学者相继提出了多种电气信号的软件频率检测算法，主要有基于正弦信号模型的检测算法、傅里叶变换检测算法、过零检测法、随即模型算法，其中随即模型算法中的卡尔曼算法适用范围较广，技术教成熟，处理得到的频率数据较精确，因此，本文采用卡尔曼算法对电力系统频率进行检查和预测。

频率是电力系统是否安全可靠运行的重要评判标准之一，本文针对电力系统频率进行精确地测量，提出利用卡尔曼算法对电力系统频率数据进行检查和预测，实时跟踪电网中频率的波动及变化，保证我国电网供电稳定和改善电网电能质量具有重要的工程应用价值。

2　卡尔曼滤波算法

卡尔曼滤波算法的核心思想是利用前一时刻最佳估计值结合现时刻观测值作线性修正，从而预测出现时刻的最佳估计[7]。卡尔曼滤波算法实质要解决的问题是要寻找在最小均方误差下XK的估计值XK。它的特点是可以用递推的方法计算XK，其所需数据存储量较小，便于进行实时处理。综上所述，卡尔曼滤波算法采用预测方程和测量方程对系统状态进行估计[8]。

3　向量卡尔曼滤波与预测算法

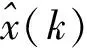
(1)

滤波误差的协方差矩阵为：

P(k)=[e(k)eT(k)]=

(2)

预测误差向量为：

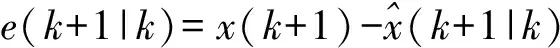
(3)

其预测协方差矩阵为：

P(k+1|k)=Ee(k+1|k)eT(k+1|k)

(4)

滤波估计方程：

x(k)=Ax(k-1)+k(k)y(k)-CAx(k-1)

(5)

滤波增益方程：

K(k)=P1(k)CTCP1(k)CT+R(k)T

(6)

式中，P1(k)=AP(k-1)AT+Q(k-1)滤波协方差方程：

P(k)=P1(k)-K(k)CP1(k)

(7)

向量卡尔曼滤波器以预测加修正作为其递推滤波的基本算法的。正是卡尔曼滤波器的这一特性，使得其很容易用计算机来实现对信号的实时滤波，为此，可采用软件方案来实现卡尔曼滤波。

式(5)为向量卡尔曼滤波的主程序算法，其中向量卡尔曼滤波的主程序算法主要具体步骤如下：

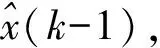
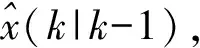
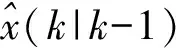
向量卡尔曼滤波的子程序算法是由(4)～(7)式构成的，其算法框图由图1所示。从图1中可以看出，向量卡尔曼滤波的子程序算法也分三步来进行。

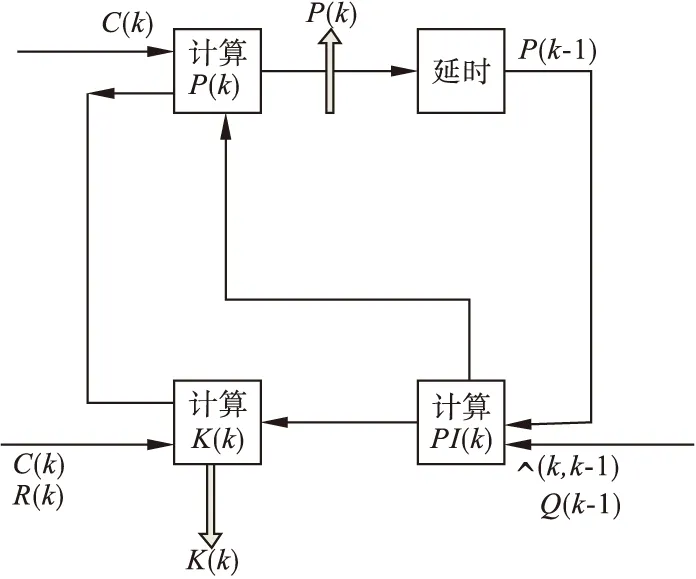
图1　向量卡尔曼滤波的子程序算法框图

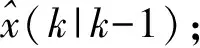
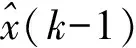
4　电网频率检测与预测

4.1　电力系统状态空间模型

考虑包含K个谐波的三相电压系统，其离散傅里叶级数形式可以表示为：

(8)

式中，k表示谐波分量的次数；kω表示k次谐波分量角频率；Uak、Ubk和Uck分别表示各相k次谐波分量有效值；φak、φbk和φck分别表示各相k次谐波分量相角；Δt为采样时间间隔，即采样频率fs=1/Δt。

由式(8)可写出修正后的三相电压系统的正序瞬时值对称分量为：

(9)

由于负序瞬时值对称分量为正序瞬时值对称分量的复共轭，故分析正序瞬时值对称分量即可获得对电网系统性能。此外，正序瞬时值对称分量包含多次谐波对称分量，在实际测量中，现场具有不可预估的噪声干扰，为减小估计误差常需要对采样信号进行滤波处理。对式(9)进行变换有：

jup(m)ejnkωΔt=Up1+ε(m)

(10)

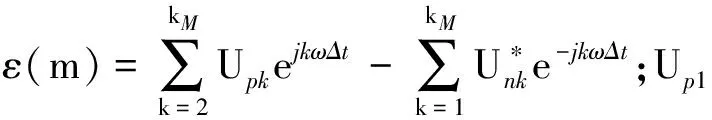
由于角频率ω不能准确得到，本文将其作为一个待估计的状态变量，这时就需对式(10)进行变换，其状态方程和量测方程可分别表示为：

X(k+1)=X(k)+V(k)

(11)

Z(k)=f(k,X(k))+W(k)

(12)

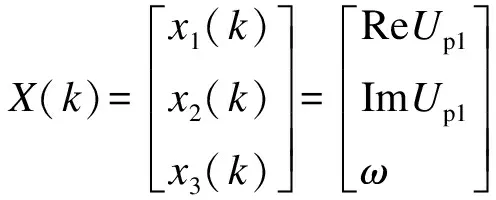
4.2　基于扩展卡尔曼滤波的估计实现

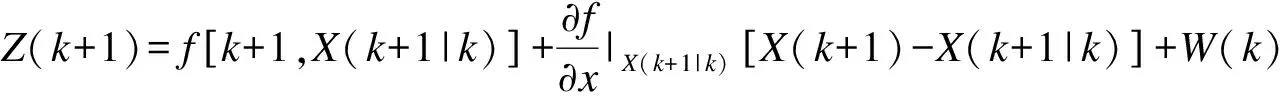
(13)

对方程进一步化简得到：

Z(k)=F(k+1)X(k+1)+Y(k+1)+W(k)

(14)

应用卡尔曼滤波基本方程，状态变量的最优估计方程最终为：

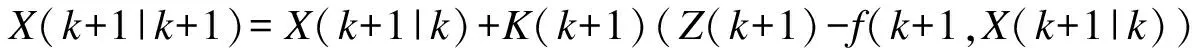
(15)

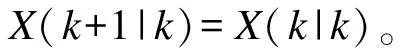
最优增益矩阵为：

K(k+1)=P(k+1)FT(k+1)[F(k+1)P(k+1|k)FT(k+1)+R(k+1)]-1

(16)

估计误差方差矩阵的递推方程为：

P(k+1|k+1)=P(k+1|k)-P(k+1|k)[P(k+1|k)+R(k+1)]-1P(k+1|k)

(17)

预测误差方差可表示为：

P(k+1|k)=P(k+1|k)+Q(k)

(18)

变量初始值取x=[0,0,0]T，估计误差方差矩阵初始值P=I。Q(k)、P(k)分别按下式进行估计：

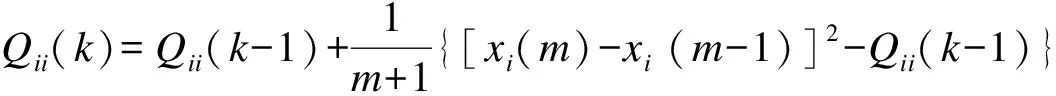
(i=1，2，3)

(19)

4.3　实例仿真分析

本文通过编程输出带多次谐波分量的电压信号其信号为：

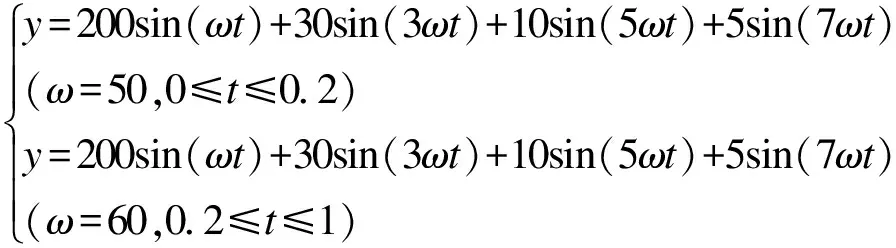
频率在0.2s处突变为60Hz，算法对频率的跟踪结果如图2所示。

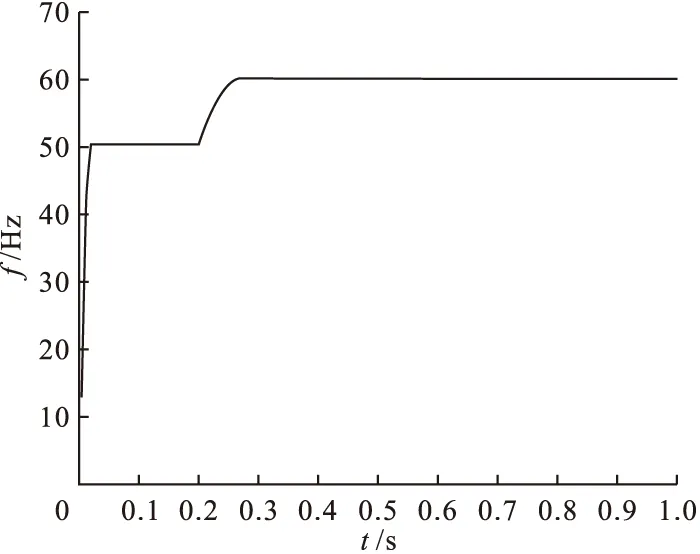
图2　频率跟踪图

由图2可得，卡尔曼滤波方法可以准确地跟踪电网频率且跟踪结果误差较小。解决了电网信号畸变时无法实现频率的正确估计问题。为电力系统的运行与控制、调节打下基础。

5　结论

本文首先分析扩展卡尔曼滤波的基本思想，从中挖掘出能够应用于电网频率检测和预测的方法；其次，对电网畸变信号的正序分量和频率进行估计，通过对电网三相电压的分析变换，利用瞬时值对称分量分析方法获得了包含基本正序分量和频率的系统非线性状态方程和量测方程；最后，利用扩展卡尔曼滤波实现了基本正序对称分量和频率的估计，并通过数据仿真进行验证。仿真结果表明本文所提出的方法可以准确估计电网信号的基本正序分量和频率，据此可实现电网电能质量的评估。

该方法是在递推过程中估计系统噪声和观测噪声大小，通过实时调节协方差，减小初始值和异常扰动对滤波的影响。但该方法是在不断的递推过程中寻求最优协方差，对状态变量的突变反应较慢，所以该方法对状态的动态跟踪性能有待于提高。

[1]张恒旭，李常刚，刘玉田，等.电力系统动态频率分析与应用研究综述[J].电工技术学报，2010，25(11)：169-176.

[2]潘迪夫，刘辉，李燕飞.基于时间序列分析和卡尔曼滤波算法的风电场风速预测优化模型[J].电网技术，2008，32(7)：82-86.

[3]周启帆,张海,王嫣然,等.一种基于冗余测量的自适应卡尔曼滤波算法[J].航空学报,2015,36(5):1596-1605.

[4]李为,李一平,封锡盛,等.基于卡尔曼滤波预测的无偏量测转换方法[J].控制与决策,2015,(2):229-234.

[5]刘育明,姚陈果,孙才新,等.基于电网频率的数字录音真伪鉴别研究[J].仪器仪表学报,2013,34(6):1434-1440.

[6]孟建辉,石新春,王毅,等.改善微电网频率稳定性的分布式逆变电源控制策略[J].电工技术学报,2015,30(4):70-79.

[7]郭钰锋,于达仁,赵婷,等.电网频率的非正态概率分布特性[J].中国电机工程学报,2008,28(7):26-31.

[8]郑为进,陈宇晨,宋萌,等.自动跟踪电网频率SPWM系统的设计[J].仪表技术与传感器,2014,(6):120-122.