若干2017年国际数学奥林匹克不等式题的精彩证明

南昌大学附属中学 (330047)

陈一君

若干2017年国际数学奥林匹克不等式题的精彩证明

南昌大学附属中学 (330047)

陈一君

本文旨在给出几道2017年国际数学奥林匹克中的不等式题的精彩证明.

例1 (2017年希腊数学奥林匹克)

已知a,b,c是正数，求证：

要证原不等式，只要证4(a+b+c)2≥3(a2+b2+c2+3ab+3bc+3ca)⟺a2+b2+c2≥ab+bc+ca,最后这一不等式显然成立，故原不等式成立.

注1：柯西不等式是最常用的基本不等式.

例2 (2017年印度数学奥林匹克)

已知x,y,z是两两不同的非负数，求证：

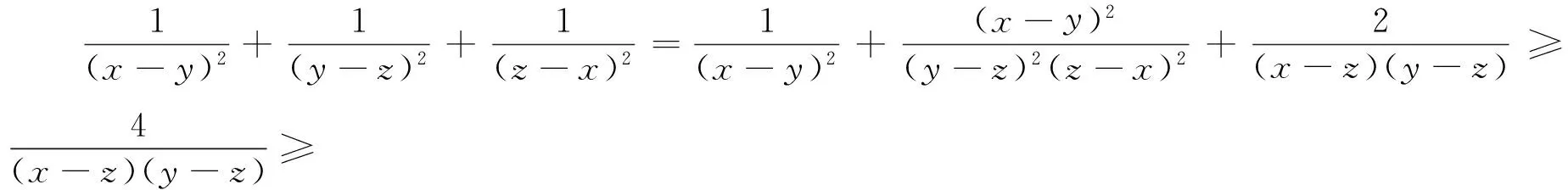
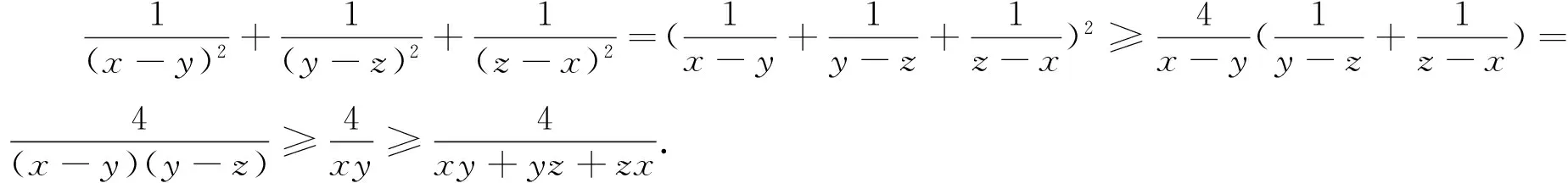
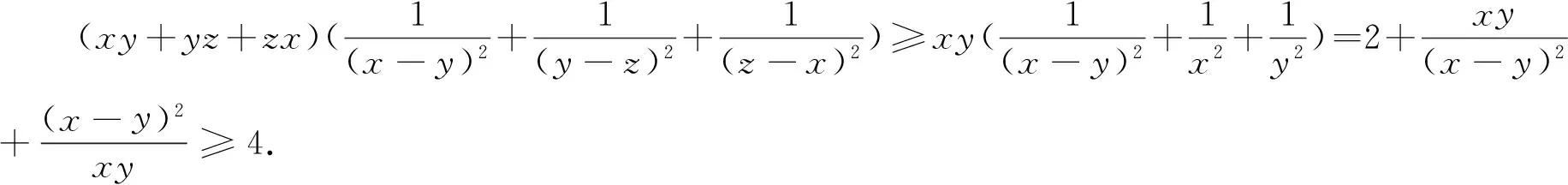
注2：排序是证明不等式的基本思想.条件的增设大大地加快了放缩的进程.

例3 (2017年越南数学奥林匹克)

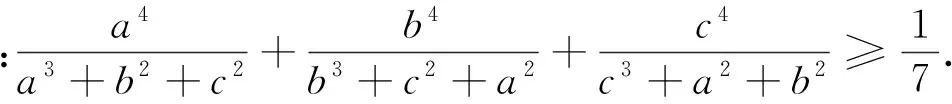
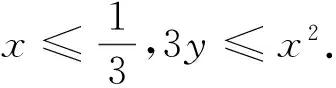
推而广之，我们有

已知a,b,c是满足a+b+c=1的正数，n是正整数，求证：

注3：减元是数学推理中的高境界.上述证明举重若轻：将三元不等式的证明化归为一元不等式来处理.

例4 (2017年印度数学奥林匹克)

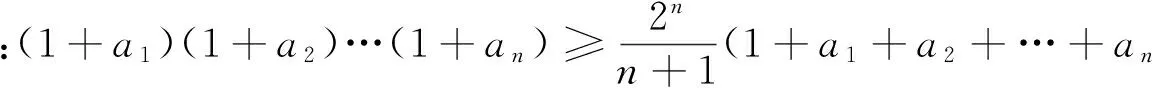
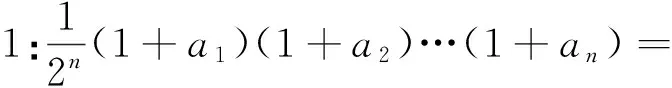
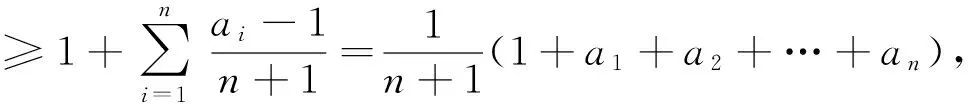
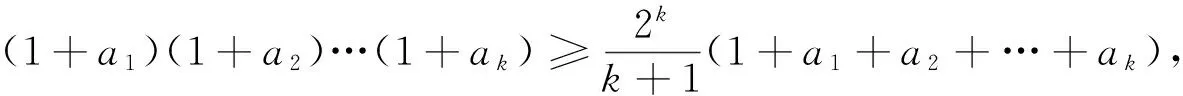
由ak+1≥1,S≥k知最后这一不等式成立.

这表明n=k+1时原不等式亦成立.所以对任意正整数n，原不等式都成立.

注4：数学归纳法的本质是递推:无穷的归纳转变为有限的演绎.

例5 (2017年印度数学奥林匹克)

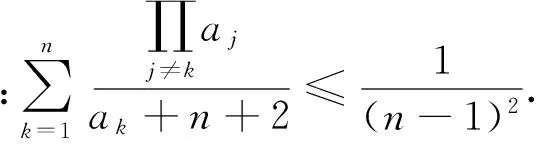
注5：本题的证明与众不同，当悉心体会.

例6 (2017年韩国数学奥林匹克)

已知f:Z→R是一个满足下列条件的函数：不等式f(x)+f(y)+f(z)≥0对于所有满足x+y+z=0的整数x,y,z都成立，求证：f(-2017)+f(-2016)+f(-2015)+…+f(2015)+f(2016)+f(2017)≥0.

证明：令2017=6k+1，则将f(±(2k-0))+f(±(4k+1))+f(∓(6k+1))≥0，f(±(2k-2))+f(±(4k+2))+f(∓(6k+0))≥0，f(±(2k-4))+f(±(4k+3))+f(∓(6k+1))≥0，…，

f(±2)+f(±5k)+f(∓(5k+2))≥0，和f(±(2k-1))+f(±(2k+1))+f(∓(4k-0))≥0,

f(±(2k-3))+f(±(2k+2))+f(∓(4k-1))≥0,f(±(2k-5))+f(±(2k+3))+f(∓(4k-2))≥0，…，f(±1)+f(±3k)+f(∓(3k+1))≥0，和f(5k+1)+f(0)+f(-5k-1)≥0，相加，便知原不等式成立.

注6：代数思想就是运用字母来代替具体数值进行思考的思维形式.本题证明是这个思想运用的一个完美范例.