两种理解哪种更合理?
2017-04-20福建省古田县第一中学352200
福建省古田县第一中学 (352200)
兰诗全
两种理解哪种更合理?
福建省古田县第一中学 (352200)
兰诗全
1 问题缘起
笔者发现在一本教学参考书有以下一例并作了错因分析.
题目 在钝角三角形ΔABC中,a=1,b=2,c=t,且C是最大角,求实数t的取值范围.
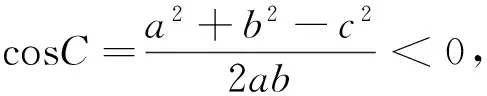

2 笔者(甲方)的理解
笔者阅后进行一番思考:以上错因分析击中要害了吗?为什么?
若按照以上错因分析的说法,即用了余弦定理后,还要再考虑三边能否构成三角形.难道三边满足了余弦定理,还未必能构成三角形?故笔者作以下探索.

证明:∵0 ∴a+b>c. 所以不难有结论:若三边满足余弦定理,则这三边一定能构成一个三角形.故参考书中的错因分析未能击中要害,未揭示问题的本质,易引起误解. 那么,以上错解究竟错在哪里呢?关键是未将问题作等价转化.并提供以下正解. 最后点击:千万别小看这小小的改动,它可击中要害,是对问题的本质理解.数学解题一定要突出方法,突出问题的本质与规律,这样才能达到真正理解. (1)以上甲方的分析有一点自圆其说、一厢情愿的意味.原来的解法只应用了余弦定理,显然没有关注到这个三角形存在的条件.只有确保1、2、t三条线段能够构成一个三角形,才能使用余弦定理讨论最大边t应满足的条件,否则属不严密.而不是甲方理解为“在应用了余弦定理后还要再考虑三边能否构成三角形”,甲方未能正确理解别人意图.甲方的分析有一个逻辑顺序的问题. (2)如何满足余弦定理?如此,是否不需要讨论三角形任意两边之和大于第三边的条件?后面的解答过程中,得到的t2<9,其实质上还是三条线段的长能够构成三角形的条件,何必多此一举,人为复杂化. (3)甲方前面的讨论,有循环论证之嫌,值得推敲.甲方给出的解答,明显的是简单问题复杂化,不符合大多数人(有条有理、由浅入深、层层递进)的思维习惯.甲方的解法非最简洁、最本质.不值得提倡. (4)对甲方的解答“击中要害”,“是对问题的本质理解”,实在看不出来,只觉得没有必要. (1)解题真的要注意逻辑顺序问题.乙方认为,原来的解法只应用了余弦定理,显然没有关注到这个三角形存在的条件.笔者认为,若三边满足余弦定理,则这三边一定能构成一个三角形,根本不必再检验三边是否满足构成三角形.数学解题中何时要检验,何时不必检验,这个逻辑顺序问题要清楚. (2)等价转化的思想是数学的重要思想之一,不要只“意会”,要落实到具体的解题之中.原来的解法根本错在没有用够余弦定理,没有对问题进行等价转化造成的错解. ∵ΔABC是钝角三角形且C是最大角,∴90° 后面的解答过程中,得到的t2<9,虽其最终还是三条线段的长能够构成三角形的条件,但有个逻辑顺序的问题.这不是多此一举,人为复杂化. (3)甲方前面的讨论,正是为了解决循环论证问题.若三边满足余弦定理,则这三边一定能构成一个三角形,根本不必再检验三边是否满足构成三角形. (4)有条有理、由浅入深、层层递进的思维不是绝对的好思维习惯.全面考虑等价转化在数学解题中往往更值得提倡. “问题将越辨越明,认识将越分析越深刻.”“讨论是学习,交流促进步.”亲爱的读者朋友们,你认为两种理解哪种更合理?你还有哪些想法?希望能展开热烈的讨论.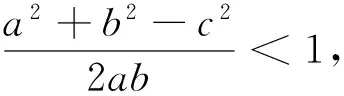

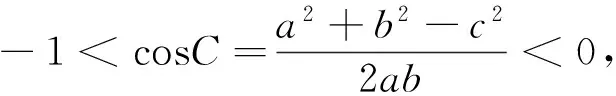

3 乙方的理解
4 笔者(甲方)的再强调
