直膨式空调系统的混合建模研究

黄小清，徐象国，晋欣桥，杜志敏

（1-上海交通大学制冷与低温研究所，上海 200240；2-浙江大学制冷与低温研究所，浙江杭州 310000）

直膨式空调系统的混合建模研究

黄小清*1，徐象国2，晋欣桥1，杜志敏1

（1-上海交通大学制冷与低温研究所，上海 200240；2-浙江大学制冷与低温研究所，浙江杭州 310000）

室内空气的温度和湿度都是影响居住者热舒适性和空调运行效率的重要因素，研究同时控制室内空气的温湿度意义重大。对于直膨式空调这样一个多变量、强耦合和非线性的系统而言，引入湿度将会显著增加系统的建模难度。单一的物理建模或者经验建模都无法同时满足精度和灵敏度的要求。本文提出了混合建模的方法，对与室内空气直接传热传质的蒸发器进行物理建模，对除蒸发器之外的系统其他部件利用神经网络（ANN）进行数学建模，模拟在变工况下空调系统产生的显热冷量和潜热冷量。结果表明，相比于单一的神经网络模型，混合模型在变工况下的模拟结果具有很好的稳定性。

直膨式空调；变工况；温湿度控制；神经网络

0 引言

室内空气的温度和湿度都是影响居住者热舒适性的重要因素，根据已有的热舒适性标准，室内空气的相对湿度应该被控制在30%～60%的范围内[1-2]。传统的直膨式空调，依靠压缩机的启-停循环，来保持室内的干球温度，却无法控制室内空气湿度。随着变频技术的发展，空调的压缩机和风机转速可以同时发生变化，从而有可能实现室内空气温度和湿度的同时控制。现在，直膨式空调的建模方法主要有两大类：物理建模方法和经验建模方法[3-7]。

物理建模是一种传统的建模方法，主要包括静态模型和动态模型。物理模型来自物理规律，因此它可以准确地反映现象的本质和系统的各项参数。但是，在建立物理模型的过程中，很多都采取了简化和假设，导致准确性降低。另外，引进室内空气湿度会显著增加建立物理模型的困难程度，需要相对较长的时间来响应，控制器的灵敏度因此降低。

随着模拟技术的不断发展，经验建模的方法也越来越多地被运用到系统建模中[4-9]，其中神经网络模型（ANN）也运用的越来越多。ANN通过对训练数据的分析，来学习输入数据和输出数据之间的关系，响应速度快。但是当数据一旦超过训练和测试的数据范围，经验模型的准确度就成了未知。SWIDER[11]的研究表明，当数据超过了经验模型的训练范围，它就无法进行准确地推断。

如前所述，物理模型和经验模型各有所长，也都有不足。物理模型应用范围广，实用性强，但建模困难；经验模型响应速度快，在多变量、非线性耦合时优势明显，但数据超出训练数据范围时会有计算的误差[12-15]。

本文提出混合建模的方法，对与室内空气之间传热传质的蒸发器进行物理建模，对空调系统除蒸发器之外的部件进行神经网络建模，达到在变工况下，同时模拟空调系统显热冷量和潜热冷量的目的。

1 实验系统

1.1 直膨式空调试验系统

本文的实验数据来自香港理工大学屋宇设备工程学院的直膨式空调系统实验台，该实验台主要由2部分组成，1个直膨式制冷单元和1个空气分布子系统，结构如图1所示。

直膨式制冷单元的主要组件，包括1个可变速的涡旋压缩机，1个电子膨胀阀（EEV），1个高效的百叶窗肋片式的蒸发器和1个风冷式翅片管式的冷凝器。蒸发器被放在送风管道里，作为冷却盘管。设计的直膨式冷却盘管的空气表面速度为2.5 m/s，名义输出冷量为9.9 kW。实际输出冷量可以在名义输出量的15%～110%之间进行调整。制冷系统的制冷剂为R22，总共5.7 kg。电子膨胀阀包括1个调节针阀，1个步进马达和1个脉冲发生器。冷凝器的风扇，封装在冷凝器的空气管道之中，也可以变速操作。1个被固态继电器控制的电子加热器用来调整在不同的实验目的下进入冷凝器的冷却空气的温度。

图1 直膨式空调系统试验台

1.2 测试精度和实验工况

实验的直膨式空调系统已经被充分的仪表化，所有温度测量都用铂电阻温度计，它的测量精度为±0.1 ℃。空气的质量流动速率用根据ANSI/ ASHRAE标准41.2生产的标准喷嘴测量，测量精度为±1.2%。所有的测量均数值化，测量数据都被记录下来进行后续的分析。

室内空气工况有两组，为干球温度（Td）25 ℃、湿球温度（Tw）20 ℃和干球温度（Td）23 ℃、湿球温度（Tw）。每种工况下，压缩机频率（f）和转速（PC）从最大转速的30%增长到80%，风机频率（f）和转速（PF）从最大转速的30%增长到90%，增长步长均为10%，实验台通过测量在2种工况下，直膨式空调系统蒸发器出口空气的干球温度和湿球温度，制冷剂在蒸发器入口和出口的温度、压力以及流量，计算出直膨式空调系统产生的显热冷量、潜热冷量以及制冷剂在蒸发器入口的焓值，每种工况产生42组实验数据，共计产生84组实验数据。

2 神经网络模型

LI等[10]的研究表明，在单一工况下，ANN模型的模拟精度很好，但对于变工况下，神经网络模型对直膨式变频空调的模拟精度问题还没有文献来说明。

本文运用MATLAB，建立了与LI等相同的2-6-6-2神经网络模型，在已有的2种工况（Td=25 ℃、Tw=20 ℃和Td=23 ℃、Tw=28 ℃）的实验数据下，以Td=25 ℃、Tw=20 ℃时42组实验数据为训练数据，Td=23 ℃、Tw=18 ℃时42组实验数据为测试数据，来验证神经网络在变工况下的计算精度。

模型以压缩机转速和风机转速为输入，显热冷量（Qs）和潜热冷量（Ql）为输出。表1给出了实验中压缩机转速和风机转速的组合情况，为了测量ANN模型的最大适用性，输入量的变化应该覆盖整个运行数据范围。因此，在研究中，压缩机转速（PC）从最大转速的30%增长到80%，风机转速（PF）从最大转速的30%增长到90%，增长速度均为10%，如表1和表2所示。因此，总共有42（6×7）个速度组合。

结果如图2和图3所示，在训练工况下，ANN的显热冷量和潜热冷量的平均相对误差分别是1.51%和1.16%，在测试工况下，显热冷量和潜热冷量的平均相对误差分别是1.55%和18.35%。该结果显示，在建立工况下，神经网络模型具有很高的可靠性，但数据超出训练范围，模拟结果就会产生很大的误差。

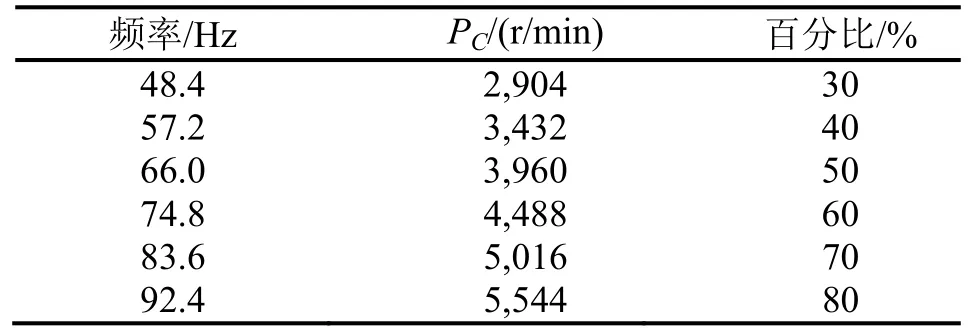
表1 压缩机速度

表2 风机速度

3 混合建模分析

混合建模的技术路线如图4所示，在不同的压缩机转速、风机转速、室内空气干球温度和湿球温度下，通过神经网络模型和物理模型的混合计算，制冷剂蒸发器出口温度的迭代，可以计算出变频直膨式空调系统的显热和潜热冷量。PF、Pc、Td和Tw分别代表风机转速、压缩机转速、室内空气干球温度和湿球温度。首先假定制冷剂蒸发器出口温度Tout，以PF和Tout为输入，蒸发器中制冷剂的质量流量qm和制冷剂蒸发器入口焓Hin为输出，建立ANN神经网络，以qm、Pc、Td和Tw为已知变量，建立蒸发器物理模型，计算出蒸发器处制冷剂和空气换热产生的显热冷量Qs和潜热冷量Ql，计算出蒸发器物理模型的制冷剂入口焓Hin’。将神经网络输出的制冷剂入口焓Hin和物理模型计算出的入口焓Hin’进行比较，如果两者差值小于0.1，则输出Qs、Ql和Tout，若两者差值较大，则更新Tout，进入混合模型，再次计算，直到满足计算要求为止。

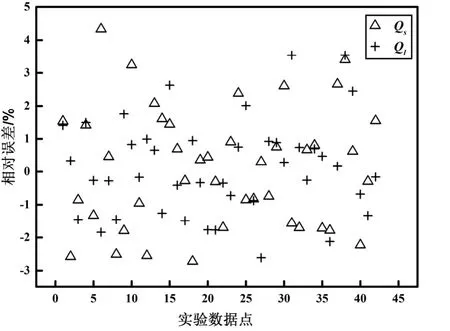
图2 ANN模型在训练工况下的Qs和Ql误差

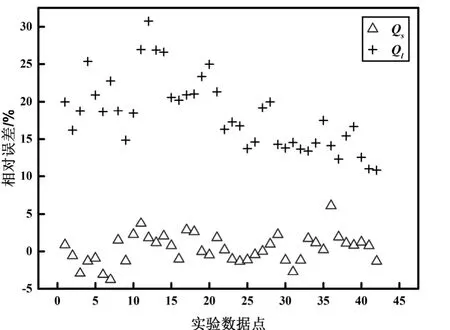
图3 ANN模型在变工况下的Qs和Ql误差

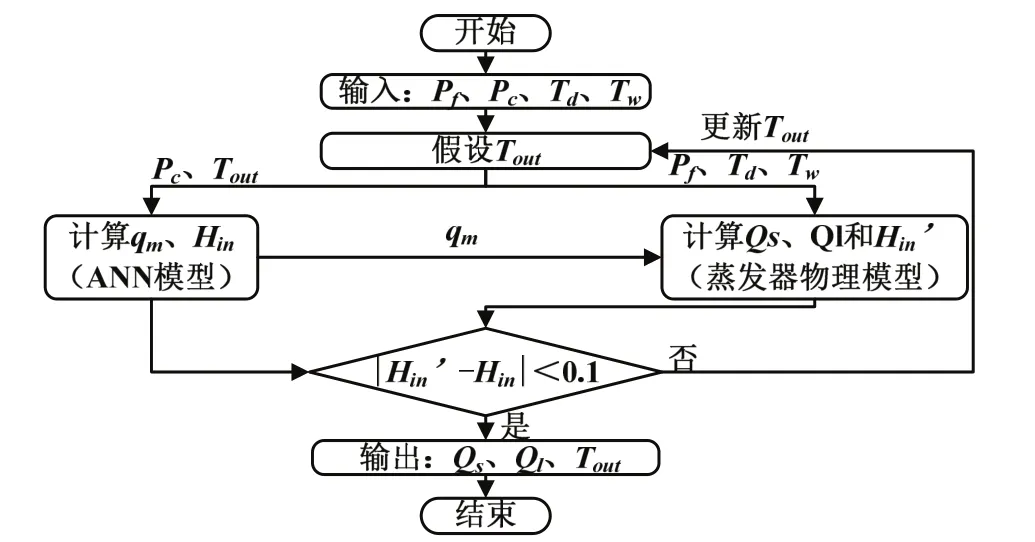
图4 混合模型计算流程图

3.1 混合模型中神经网络模型的计算精度

要使混合模型具有高的计算精度，神经网络模型和蒸发器物理模型都要同时具有高的计算精度，对于神经网络模型，以风机转速PF和蒸发器出口温度Tout为输入，蒸发器中制冷剂的质量流量qm和制冷剂蒸发器入口焓Hin为输出，建立在训练工况Td=25 ℃、Tw=20 ℃下的2-6-6-2模型，如图5所示，在训练工况下，qm和Hin的平均相对误差分别是0.18%和0.39%，以Td=23 ℃、Tw=18 ℃的实验数据为测试数据，计算混合模型的神经网络部分在变工况下的平均相对误差，结果如图6所示，制冷剂的质量流量qm和制冷剂蒸发器入口焓Hin的平均相对误差分别是1.76%和1.54%，神经网络部分具有很高的计算精度。

图5 神经网络模型训练工况下qm和Hin的相对误差

图6 神经网络模型测试工况下qm和Hin的相对误差

3.2 混合模型在变工况下的计算精度

混合模型中的神经网络模型已经具有很高的精度，在此基础上建立蒸发器物理模型并搭建混合模型。混合模型的训练工况为Td=25 ℃、Tw=20 ℃。首先测试混合模型在训练工况下显热冷量Qs和潜热冷量Ql的计算精度，结果如图7所示；在训练工况下，混合模型Qs和Ql的平均相对误差分别是3.04%和11.24%。然后测试混合模型在Td=23 ℃和Tw=18 ℃下显热冷量Qs和潜热冷量Ql的计算精度，结果如图8所示，在测试工况下，混合模型Qs和Ql的平均相对误差分别是4.18%和13.47%。

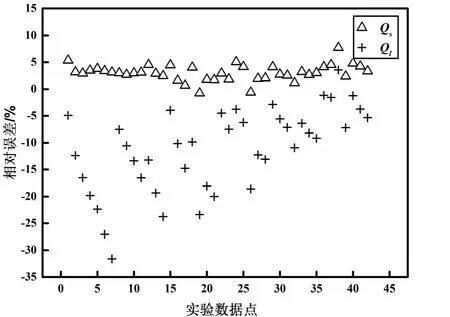
图7 混合模型训练工况下Qs和Ql相对误差

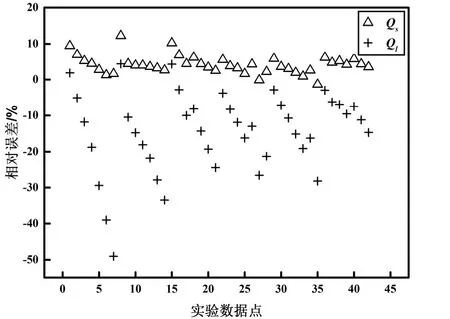
图8 混合模型测试工况下Qs和Ql相对误差

3.3 神经网络模型和混合模型的比较

神经网络模型虽然建模简单，但是当测试数据超出训练数据范围时，神经网络模型的计算精度就会显著下降，计算结果很不稳定。所以，直接用神经网络模型计算空调系统的显热冷量和潜热冷量难以满足精确度和稳定性的要求。在混合模型中，神经网络模型通过计算制冷剂质量流量和制冷剂进入蒸发器时的入口焓值，结合蒸发器的物理模型来间接参与到空调系统的显热冷量和潜热冷量计算中，虽然混合模型在计算潜热冷量时的计算误差依然达到了10%；但是，在变工况的情况下，混合模型的潜热冷量Qs和潜热冷量Ql计算精度仍然在同一个数量级上，其结果是稳定的，为以后混合模型的修正打下了基础。神经网络模型和混合模型在测试工况和训练工况下的计算误差情况如表3所示。

表3 神经网络模型和混合模型在测试工况和训练工况下的计算误差

4 结论

物理模型运用数学方程来描述物理过程，应用范围广但建模困难；神经网络模型在单一工况下显热冷量和潜热冷量的计算精度都较高，但是，在变工况下，潜热冷量的计算精度和稳定性都无法达到要求。

本文将物理模型和神经网络模型结合起来，将与空气之间直接传热传质的蒸发器进行物理建模，将直膨式空调的其余部分进行神经网络建模，来模拟变工况下直膨式空调产生的显热冷量和潜热冷量，从而实现室内空气温湿度的同时控制。

相比于神经网络模型，混合模型虽然计算精度有待提高，但是计算的稳定性却很好。在混合模型中，神经网络部分的计算精度已经很好，要想进一步提高混合模型的计算精度，应该对蒸发器的物理建模部分进行进一步优化，主要包括制冷剂在蒸发器中的压降，制冷剂干度变化引起的制冷剂侧换热系数的变化以及蒸发器表面的除湿过程等。

[1] XIA L, CHAN MY, DENG SM, et al. Dehumidification effects in the superheated region (SPR) of a direct expansion (DX) air cooling coil[J]. Energy Convers Manage, 2009, 50(12): 3063-3070.

[2] THEERAKULPISUT S, PRIPREM S. Modeling cooling coils[J]. International Communications in Heat and Mass Transfer, 1998, 25(1): 127-137.

[3] 李志量, 陈新强, 马金平, 等. 空调长效节能特性评价方法的研究[J]. 制冷技术, 2013, 33(2): 27-29.

[4] 孙浩然, 任滔, 李智强, 等. 结合用户数据的空调器仿真平台构建[J]. 制冷技术, 2014, 34(4): 31-37.

[5] KRAKOW K I, LIN S, ZENG Z S. Temperature and humidity control during cooling and dehumidifying by compressor and evaporator fan speed variation[J]. ASHRAE Trans, 1995, 101(1): 1283-297.

[6] 黄晓斌, 杨伟国. 变频空调器的模糊CMAC神经网络控制[J]. 制冷技术, 2004, 24(3): 34-36.

[7] NAVARRO´J, BERBEGALL V, VERDU G, et al. A low data requirement model of a variable-speed vapour compression refrigeration system based on neural network[J]. International Journal of Refrigeration, 2007, 30(8): 1452-1459.

[8] LI H, JOENG S K, YOON J I, et al. An empirical model for independent control of variable speed refrigeration system[J]. Applied Thermal Engineering, 2008, 28(14/15): 1918-1924.

[9] 李树江, 吕梁年, 王向东, 等. 暖通空调制冷系统建模与控制现状及发展趋势[J]. 沈阳工程大学学报, 2007, 29(3): 300-307

[10] LI N, XIA L, DENG S M, et al. Steady-state operating performance modeling and prediction for a direct expansion air conditioning system using artificial neural network[J]. Building Services Engineering Research and Technology, 2012, 33(3): 281-292.

[11] SWIDER D J. A comparison of empirically based steady-state models for vapor-compression liquid chillers[J]. Applied Thermal Engineering, 2003, 23(5): 539-556.

[12] 李晓佳, 周悦. 空调制冷系统的建模研究[J]. 洁净与空调技术, 2009(1): 41-43.

[13] WANG X F, XU X G. A control-oriented hybrid model for a direct expansion air conditioning system[R]. The 24thinternational congress of refrigeration: ICR, 2015.

[14] WANG Y W, CAI W J, SOH Y C, et al. A simplified modeling of cooling coils for control and optimization of HVAC systems[J]. Energy Conversion and Management, 2004, 45(18): 2915-2930.

[15] MARTINS-COSTA M L, PARISE J A R. Three zone simulation model for air-cooled condensers[J]. Heat Recovery System, 1993, 13(2): 97-113.

Study on Hybrid Modeling of Direct Expansion Air Conditioning System

HUANG Xiaoqing*1, XU Xiangguo2, JIN Xinqiao1, DU Zhimin1
(1-Institution of Refrigeration and Cryogenics, Shanghai Jiao Tong University, Shanghai 200240, China; 2- Institution of Refrigeration and Cryogenics, Zhejiang University, Hangzhou, Zhejiang 310000, China)

Both the indoor temperature and humidity are key factors influencing on the residents’ thermal comfort and the operating efficiency of air conditioner, and it is significant to study simultaneously to control indoor air temperature and humidity. For a nonlinear, multivariate and complex system like a direct expansion (DX) air conditioning (A/C) system, introducing humidity will increase the difficulties of modeling sharply. Neither physical model nor empirical model can meet the requirement of high accuracy and high sensitivity. A hybrid modeling method was proposed by using mathematics to model the evaporator which transfers heat and mass directly with indoor air and using the artificial neural network (ANN) to model the rest components, in order to simulate the sensible heat transfer and latent heat transfer of direct expansion air conditioning system under variable working conditions. The results indicated that the hybrid model could provided a stable result under variable working condition compared with single ANN model.

Direct expansion air conditioner; Variable operating condition; Temperature and humidity control; Artificial neural network

10.3969/j.issn.2095-4468.2017.01.108

*黄小清（1993-），女，硕士研究生。研究方向：制冷系统能耗模拟和优化。联系地址：上海市东川路800号机动学院C楼155，邮编：200240。电话：15821196530。E-mail：huangxiaoqing@sjtu.edu.cn。

本论文选自2016年第九届全国制冷空调新技术研讨会。