基于ANN和LSSVR的造纸废水处理过程软测量建模

汪 瑶 徐 亮 殷文志 胡慕伊 黄明智 刘鸿斌,2,*

(1.南京林业大学江苏省制浆造纸科学与技术重点实验室,江苏南京,210037；2.华南理工大学制浆造纸工程国家重点实验室,广东广州,510640；3.中山大学水资源与环境系,广东广州,510275)

基于ANN和LSSVR的造纸废水处理过程软测量建模

汪 瑶1徐 亮1殷文志1胡慕伊1黄明智3刘鸿斌1,2,*

(1.南京林业大学江苏省制浆造纸科学与技术重点实验室,江苏南京,210037；2.华南理工大学制浆造纸工程国家重点实验室,广东广州,510640；3.中山大学水资源与环境系,广东广州,510275)

针对造纸废水处理系统的时变性、非线性和复杂性等特点,将人工神经网络(ANN)和最小二乘支持向量回归(LSSVR)分别用于造纸废水处理过程中的软测量建模,实现造纸废水处理过程中出水化学需氧量和出水悬浮固形物浓度的预测。ANN采用误差反向传播算法建模,LSSVR通过粒子群优化算法进行模型参数优化。结果表明,与ANN模型预测结果相比,LSSVR模型预测结果的均方根误差降低了50%以上,相关系数提高了近10%,表明LSSVR模型在造纸废水处理过程中的预测精度高于ANN模型。

人工神经网络；最小二乘支持向量回归；造纸废水处理；软测量建模；粒子群优化算法

通常采用物理法或生化法处理造纸废水,该处理过程具有非线性、时变性、不确定性、复杂性和滞后性等特点[1]。因而,采用机理分析和数学推导的方法难以获得精确的数学模型[2],特别是与出水水质指标相关的关键参数无法实现在线测量,这直接影响废水处理过程的实时控制和优化操作。将软测量技术应用于造纸废水处理过程,建立出水水质关键参数的软测量模型,可有效解决这一难题[3]。

目前,软测量建模的主要方法有机理建模、回归分析、模糊建模和神经网络建模等[4- 6]。其中,人工神经网络(Artificial Neural Network,ANN)近年来已成功应用在造纸废水处理过程软测量建模中。李迪等[7]采用ANN对造纸废水处理过程进行动态建模；马邕文等[8]提出了利用模糊神经网络模型对废水处理过程的化学需氧量进行控制及预测；李伟奖等[9]针对误差反向传播算法收敛慢、易陷入局部极小等缺点,提出用遗传算法进行全局寻优。

支持向量机(Support Vector Machines,SVM)是一种基于统计学习理论的新型学习机。SVM利用结构最小化原理较好地解决了小样本、非线性、高维数、局部极小等实际问题,目前已成为污水处理过程建模领域的研究热点[10-13]。最小二乘支持向量回归(Least Square Support Vector Regression,LSSVR)是SVM的改进,其在SVM的基础上降低了计算复杂度,有效提高了学习速度,更加适用于工业过程软测量建模的研究[14]。张世峰等[15]提出一种基于LSSVR的出水水质软测量模型,并将其应用于污水处理过程中溶解氧浓度的控制。

本课题应用ANN和LSSVR这2种方法分别建立造纸废水处理过程的软测量模型,实现造纸废水处理过程中出水化学需氧量(CODeff)和出水悬浮固形物(SSeff)浓度的预测。

1 ANN和LSSVR的原理

1.1 ANN原理

ANN算法多种多样，其中应用最为广泛的是误差反向传播(BP)网络,其主要由输入层、隐含层和输出层构成,如图1所示。BP网络的工作原理是输入信号的正向传播和误差信号的反向传播,通过权重修正使得式(1)中误差函数E趋于最小。

(1)

式中,m为学习样本数,dk表示第k个节点的期望值,yk表示第k个节点的输出值。

式(1)递推学习算法如下：

(2)

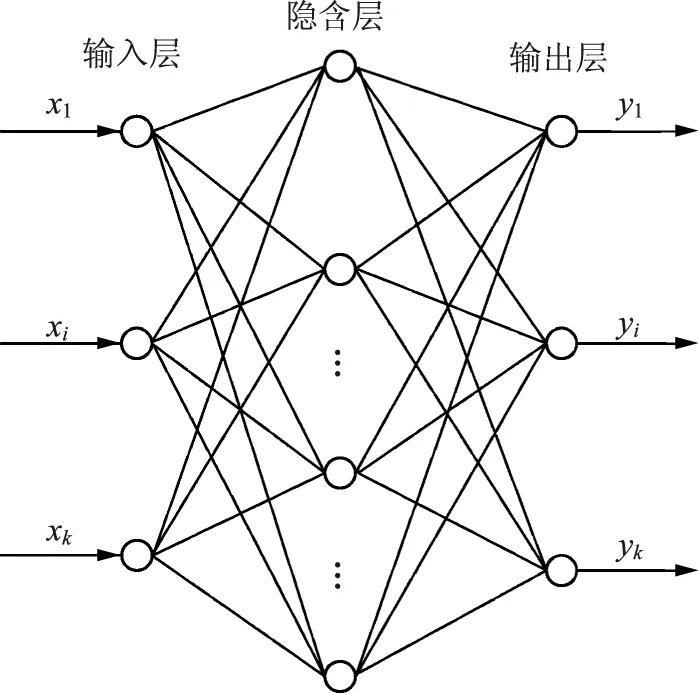
图1 BP网络结构

1.2 LSSVR原理

SVM的原理是把原始样本空间通过核函数映射到高维特征空间,然后在此空间中运用结构风险最小化思想求解凸优化问题。SVM的数学模型是一个典型的二次规划问题。由于标准的SVM模型需要求解二次规划问题,所以在大样本数据情况下,其运算量大,所需支持的向量个数也较多,导致模型较复杂,不易于模型的推广使用。Suykens等[17]在SVM基础上提出了LSSVR模型。相对于SVM,LSSVR模型中的约束是等式约束,在优化目标函数中选取了误差平方和的形式,将原来需要解决的二次规划问题通过最优性条件转化为线性方程组求解问题,大大降低了计算复杂度。在非线性系统建模方面,LSSVR模型更具优势,其基本思想[14]如下。

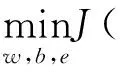
s.t.y(x)=ωTφ(xi)+b+ξi

(3)

式中,ω是权系数向量,C是正规化参数,φ(xi)是输入空间到高维空间的非线性映射函数,b为阈值,ξi为拟合误差。引入αi(1,2,3,…,n),定义拉格朗日函数为：

(4)

又根据KKT(Karush-Khun-Tucker)条件得到：

(5)

通过消元法消去ω和ξi可以得到如下矩阵方程：

(6)

式中,P1×n是1×n的单位行向量；Pn×1是n×1的单位列向量；K(xi+xj)为满足Mercer条件的核函数,其中i、j=1,2,…,n；E为n×n单位阵；y=[y1,y2，…,yn]T；α=[α1,α2,…,αn]T,运用最小二乘法可以求得b和α的值,最终求得回归函数如下：

(7)

其中,K(xi,xj)称为核函数。核函数的种类很多,常用的有：多项式函数,RBF函数,线性函数,Sigmoid函数等。笔者选用RBF函数K(xi,xj)=e-(-xi-xj)2/(2σ2),σ是RBF函数的核函数宽度。

1.3 粒子群优化算法确定系统参数

由于建立回归模型时选用RBF核函数,其模型参数核函数宽度σ和正规化参数C组成对训练时的平均误差影响较大。因此,用合适的参数选取方法代替人工试凑法将大为缩短建模时间并给予参数选取以理论支持[18]。在此,采用粒子群优化(Particle Swarm Optimization,PSO)算法确定这2个参数。

假设,对由m个粒子组成的群体进行搜索,粒子i在群体中的位置为Xi=(x1,x2,…,xn),运动速度为Vi=(v1,v2,…,vn)。每个粒子都有一个目标函数决定的适应度值(fitness value)。粒子群初始化为一群随机粒子,通过迭代找到最优解,在每一次的迭代中,粒子通过跟踪2个“极值”来更新自己,一个为个体极值(pbest),是粒子本身找到的最优解；另一个为全局极值(gbest),是整个群体目前找到的最优解。粒子群更新公式如下：

Vi+1=Vi+c1·rand·(pbesti-xi)+c2·rand·(gbesti-xi)

(8)

Xi+1=xi+Vi

(9)

式中,rand是介于(0，1)间的随机数；c1和c2是学习因子,通常取c1=c2=2。通过不断更新粒子,直至满足迭代结束条件之后,得到的粒子最优位置,即为LSSVR模型对应的最优参数值σ和C。PSO算法流程图如图2所示。

图2 PSO算法流程图

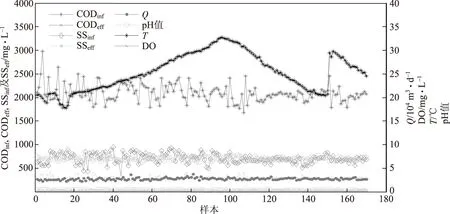
图3 造纸废水处理过程数据

2 建模与结果分析

2.1 造纸废水处理软测量模型的建立

2.1.1 废水数据分析

本实验的建模数据来源于广东某造纸厂的废水处理车间,数据是该厂于2006年3月15日—12月21日期间在好氧段出水处得到的,共计170组数据,如图3所示。从图3可看出,样本中共含有8个变量,分别为进水化学需氧量(CODinf)、出水化学需氧量(CODeff)、进水悬浮固形物浓度(SSinf)、出水悬浮固形物浓度(SSeff)、流量Q、温度T、溶解氧量(DO)和pH值,其中CODinf、SSinf、pH值、Q、T和DO作为系统的输入量,分别预测CODeff和SSeff。

2.1.2 ANN预测模型的建立

从数据样本中,随机选取90组样本进行训练,剩下的80组作为检验样本来做预测。根据经验,笔者采用(6,16,1)的网络结构。在BP网络经过训练收敛后,利用训练好的网络模型对剩下的数据进行仿真,结果如图4和图5所示。

2.1.3 LSSVR预测模型的建立

与ANN选用相同的训练集和预测集。在初始时刻选择参数的优化范围0.1≤σ≤500,1≤C≤1000,以及选定粒子群规模为70和最大的迭代次数为200。通过对训练数据的学习及PSO算法对LSSVR的参数优化调整[19],得到预测CODeff和SSeff时的最优参数,分别为σ1=28.5,C1=3.9；σ2=56.5,C2=2.4。预测结果如图6和图7所示。

2.2 结果分析

为了比较ANN和LSSVR这2种模型的性能,采用相关系数(R)和均方根误差(RMSE)作为评价指标来评价模型的预测效果。其中,R用来反映预测值与测量值之间相关的密切程度,见式(10)；RMSE用来衡量预测值与测量值之间的偏差,见式(11)。最终得到的R和RMSE的值如表1所示。

(10)

(11)

图4 ANN模型的CODeff预测值与测量值对比

图5 ANN模型的SSeff预测值与测量值对比

图6 LSSVR模型的CODeff预测值与测量值对比

图7 LSSVR模型的SSeff预测值与测量值对比

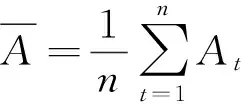
由图4与图6的对比和图5与图7的对比可以看出,LSSVR模型所得预测值更接近测量值。由表1所示的R和RMSE可知,与ANN模型相比,LSSVR模型预测CODeff时的RMSE降低了52%,在预测SSeff时的RMSE降低了56%,且LSSVR模型得到的相关系数R提高了近10%。以上说明,LSSVR模型预测结果的精度高于ANN模型预测结果。

表1 ANN和LSSVR模型预测结果的性能指标对比

虽然LSSVR模型预测的效果较好,但由表1也可以看出,这2种模型所得相关系数R均不高。索幸仪等[20]提出了一种基于模糊核聚类的多最小二乘支持向量的软测量建模方法,用模糊核聚类算法对输入数据进行分类,针对每个聚类子集用LSSVR建立子模型。这种多模型的建模方法把难以用一个模型表达的复杂系统转换为用多个简单模型逼近,可大大提高模型的精度。由此思考,将本研究中的6个输入量进行分类,建立多个LSSVR子模型以提高模型精度,这可以作为将来的研究方向。

3 结 论

3.1 采用人工神经网络(ANN)和最小二乘支持向量回归(LSSVR)2种方法分别对造纸废水处理过程中的出水COD和SS进行预测。通过对比这2种方法的预测结果发现,在相同的训练集和预测集的情况下,LSSVR模型的预测结果比ANN模型更为精确。这说明,在小样本的训练中,LSSVR模型效果更好。

3.2 采用粒子群优化(PSO)算法对LSSVR模型参数进行优化,解决了LSSVR在参数选择时用人工试凑法的盲目性,大大减少了参数选择的时间,结果也更为精确。

3.3 ANN模型和LSSVR模型所得相关系数R均不高。如何利用其他方法,如多模型建模方法等,对模型进行优化以提高模型的预测精度,是今后研究的方向。

[1] Zhang Q, Stanley S J. Real-time water treatment process control with artificial neural networks[J]. Journal of Environmental Engineering, 1999, 125(2): 153.

[2] 刘建勇, 周雪飞, 薛 罡, 等. 智能控制在污水处理中的应用现状及展望[J]. 中国给水排水, 2002, 18(11): 22.

[3] 赵 超, 戴坤成, 王贵评, 等. 基于AWLS-SVM的污水处理过程软测量建模[J]. 仪器仪表学报,2015, 36(8): 1792.

[4] 徐文艳, 王 豪. 基于机理建模的聚醋酸乙烯浓度软测量技术[J]. 化工自动化及仪表, 2010, 37(7): 70.

[5] 俞金寿. 软测量技术及其应用[J]. 自动化仪表, 2008, 29(1): 1.

[6] 于 涛, 王建林, 何 坤, 等. 基于MPCA-GP的发酵过程分阶段软测量建模方法[J]. 仪器仪表学报, 2013, 34(12): 2703

[7] 李 迪, 唐 辉, 万金泉, 等. 基于ANN的废纸造纸废水处理过程的动态建模[J]. 华南理工大学学报： 自然科学版, 2005, 33(12): 42.

[8] 马邕文, 黄明智, 万金泉, 等. 模糊神经模型对废水处理过程COD的预测及控制[J]. 中国造纸学报, 2008, 23(4): 113.

[9] 李伟奖, 马邕文. 基于遗传算法和BP网络的造纸废水处理预测研究[J]. 中国造纸学报, 2010, 25(1): 67.

[10] 王启超. 基于组合核函数支持向量机的软测量技术及其应用研究[D]. 南昌： 江西理工大学, 2011.

[11] 苏书惠, 张绍德, 谭敬辉. 基于支持向量机的污水处理软测量算法的研究[J]. 自动化与仪器仪表, 2009, 4(6): 6.

[12] 张 杰, 张建秋, 冯 辉, 等. 支持向量机和神经网络联合软测量SBR污水处理中COD的方法[J]. 传感技术学报, 2009, 22(10): 1519.

[13] 刘成忠, 韩俊英. 基于邻域粗糙集的支持向量机在污水处理故障诊断中的应用[J]. 甘肃农业大学学报, 2013, 48(3): 176

[14] 顾燕萍, 赵文杰, 吴占松. 最小二乘支持向量机的算法研究[J]. 清华大学学报： 自然科学版, 2010, 50(7): 1063.

[15] 张世峰, 杨 成, 李晓明. 基于LSSVM逆系统在污水处理系统DO控制中的研究[J]. 工业控制计算机, 2013, 26(4): 66.

[16] 韩力群. 人工神经网络理论、 设计及应用[M].北京：化学工业出版社, 2007.

[17] Suykens J A K, Brabanter J D, Lukas L, et al. Weighted least squares support vector machines: robustness and sparse approximation[J]. Neurocomputing, 2002, 48(1/2/3/4): 85.

[18] 任洪娥, 霍满冬. 基于PSO优化的SVM预测应用研究[J]. 计算机应用研究, 2009, 26(3): 867.

[19] 徐方舟, 潘 丰. 基于PSO-LSSVM污水处理系统出水数据的软测量[J]. 江南大学学报： 自然科学版, 2010, 9(3): 253.

[20] 索幸仪, 侍洪波. 基于多模型模糊核聚类方法的污水处理过程软测量建模[J]. 华东理工大学学报： 自然科学版, 2010, 36(5): 732.

(责任编辑：陈丽卿)

Soft Sensor Modeling of Papermaking Wastewater Treatment Processes Based on ANN and LSSVR

WANG Yao1XU Liang1YIN Wen-zhi1HU Mu-yi1HUANG Ming-zhi3LIU Hong-bin1,2,*

(1.JiangsuProvincialKeyLaboratoryofPulpandPaperScienceandTechnology,NanjingForestryUniversity,Nanjing,JiangsuProvince, 210037； 2.StateKeyLaboratoryofPulpandPaperEngineering,SouthChinaUniversityofTechnology,Guangzhou,GuangdongProvince, 510640; 3.DepartmentofWaterResourcesandEnvironment,SunYat-SenUniversity,Guangzhou,GuangdongProvince, 510275)

(*E-mail: hbinjm@163.com)

Concerning the time-varying, nonlinear, and complex characteristics of papermaking wastewater treatment systems, soft sensor modeling methods based on artificial neural network (ANN) and least squares support vector regression (LSSVR) were used to predict effluent chemical oxygen demand and suspended solids in a papermaking wastewater treatment process. ANN model was established by using error back propagation algorithm. The particle warm optimization was used to optimize model parameters in the LSSVR model. The results showed that the root mean square error of LSSVR model reduced by more than 50% compared with that of ANN model, and the correlation coefficient of LSSVR model increased by about 10% compared with that of ANN model. These results indicated that the LSSVR model had better prediction performance and higher accuracy compared to the ANN model in papermaking wastewater treatment process．

artificial neural network; least squares support vector regression; papermaking wastewater treatment; soft sensor modeling; particle swarm optimization

2016- 01-25

制浆造纸工程国家重点实验室开放基金资助项目(201610)；南京林业大学高层次人才科研启动基金(163105996)；江苏省制浆造纸科学与技术重点实验室开放基金项目(201530)。

汪 瑶,女,1992年生；在读硕士研究生；主要研究方向：制浆造纸过程与控制。

*通信联系人：刘鸿斌,E-mail:hbinjm@163.com。

X793

A

1000- 6842(2017)01- 0050- 05