基于差分隐私的频繁序列模式挖掘算法
2017-04-20李艳辉王国仁
李艳辉,刘 浩,袁 野,王国仁
(东北大学 计算机科学与工程学院,沈阳110819)
(*通信作者电子邮箱lyhneu506822328@163.com)
基于差分隐私的频繁序列模式挖掘算法
李艳辉*,刘 浩,袁 野,王国仁
(东北大学 计算机科学与工程学院,沈阳110819)
(*通信作者电子邮箱lyhneu506822328@163.com)
针对当数据集含有敏感信息时,直接发布频繁序列模式本身及其支持度计数都有可能泄露用户隐私信息的问题,提出一种满足差分隐私(DP)的频繁序列模式挖掘(DP-FSM)算法。该算法利用向下封闭性质生成候选序列模式集,基于智能截断方法从候选模式中挑选出频繁的序列模式,最后采用几何机制对所选出模式的真实支持度添加噪声进行扰动。另外,为了提高挖掘结果的可用性,设计了一个阈值修正的策略来减小挖掘过程中的截断误差和传播误差。理论分析证明了该算法满足ε-差分隐私。实验结果表明了该算法在拒真率(FNR)和相对支持度误差(RSE)两个指标上明显低于对比算法PFS2,有效地提高了挖掘结果的准确度。
频繁序列挖掘;差分隐私;隐私保护;几何机制;数据挖掘
0 引言
频繁序列挖掘(Frequent Sequence Mining,FSM)是数据挖掘研究领域的一个重要课题,其目的是找出相对时间或其他顺序频繁出现在数据集中的模式,是关联规则、相关性分析、分类、聚类等多种数据挖掘任务的基础。随着大量序列数据的收集和存储,频繁序列模式可以为诸如市场分析、需求预测等数据分析任务提供大量有价值的信息。然而,频繁序列模式本身和其相应支持度计数都有可能泄露隐私信息。
传统隐私保护方法大多基于k-匿名[1]和划分,这类方法均需要对攻击模型和攻击者的背景知识预先作出假设,无法提供一种有效且严格的方法来证明其隐私保护水平。此外,随着诸如组合攻击和前景知识攻击等新型攻击模型的出现,对这些方法的有效性提出了严峻挑战。差分隐私(Differential Privacy,DP)[2]是Dwork在2006年提出的一种基于数据失真,独立于攻击者背景知识和计算能力的强隐私保护模型,近年来已成为隐私保护领域的一个研究热点。
当前已有很多文献对差分隐私下的频繁序列模式挖掘进行了深入研究。文献[3-4]提出了两种非交互框架下的频繁序列模式挖掘方法,其关注于序列数据库的发布,挖掘结果效用性较差。不同于文献[3-4],文献[5-6]提出交互式框架下的频繁序列模式挖掘方法,分别关注于挖掘连续序列模式和一般化的频繁序列挖掘。
尽管文献[6]提出的差分隐私下的频繁序列模式挖掘算法PFS2(differentially Private Frequent Sequence mining via Sampling-based Candidate Pruning)可以解决频繁序列模式挖掘过程中存在的隐私泄露问题。但是,该算法在重构序列数据库时未考虑不同候选序列重要程度的差异性,导致算法准确度低,挖掘结果效用性差。
针对上述问题,本文基于差分隐私,提出一种具有高效用性的频繁序列挖掘策略——DP-FSM(Differential Private Frequent Sequence Mining)算法。该算法主要从两个方面提高挖掘结果的准确度。首先,基于候选集中不同候选序列重要程度的差异性,提出了一种启发式的方法设计打分函数来区分不同候选序列的重要程度,从而能在序列截断时使具有高优先级的候选序列优先保留;其次,针对挖掘频繁序列模式的误差问题,提出一种阈值修正策略,通过判断某序列是否频繁和判断某序列是否用于产生候选序列而设置不同的阈值以减小误差。
1 相关工作
根据挖掘的对象不同,目前差分隐私保护下的频繁模式挖掘研究主要分为频繁项集挖掘和频繁序列挖掘,其中频繁序列挖掘与本文讨论的问题最为相关。
1.1 频繁项集挖掘
近年来,差分隐私下的频繁项集挖掘已取得一些重大的研究进展。Bhaskar等[7]提出了两种满足差分隐私的top-k频繁项集挖掘策略。这两种方法借鉴截断频率的思想,分别运用拉普拉斯机制与指数机制。Li等[8]提出一种可用于高维数据的PrivBasis算法,该算法结合θ-基与映射技术在保证计算性能的前提下实现差分隐私保护。张啸剑等[9]提出一种采用后置处理技术对噪声计数进行求精处理,使输出结果满足一致性要求的方法,该方法能获得较好的可用性。Zeng等[10]针对长事务会导致高查询敏感性的缺陷,提出了一种基于事务截断技术提高结果可用性的贪婪方法SmartTrunc。上述算法是交互式框架下的频繁项集挖掘方法,但它们只适用于特定的情境,而项集与序列的差异使得这些算法并不适用于挖掘频繁序列模式。
Chen等[11]提出了一种基于上下文无关分类树,结合自顶向下的树划分方法来发布数据集;Lee等[12]提出了一种使用前缀树来隐私地发布频繁项集的方法。这两种算法是非交互式框架下的频繁项集挖掘方法,这类方法通过隐私地发布数据集来支持频繁项集挖掘。
1.2 频繁序列挖掘
Chen等[3]提出一种基于前缀树的方法隐私地发布轨迹数据集,用于支持频繁序列挖掘。此外,他们在文献[4]中还提出了一种基于变长n-gram模型来发布序列数据集的方法。这种方法主要利用变长n-gram模型提取序列数据库的必要信息,利用探索树减少添加噪声的数量。这两种方法与本文方法的不同之处在于前者关注于序列数据库的发布,而本文方法则关注于频繁序列的发布。
Bonomi等[5]提出了一个满足差分隐私保护的两阶段的频繁连续序列挖掘策略。该方法首先利用一个前缀树来找到所有的候选序列,然后利用数据库局部转换技术细化候选序列的支持度。和这种方法只针对连续序列挖掘相比,Xu等[6]提出了一个关注于一般化的频繁序列挖掘,忽略序列中的项是否连续的算法PFS2。这个算法的核心是利用一个基于采样的候选剪枝技术来减小候选序列的数目。该技术的主要思想是使用候选序列在样本数据库中的局部噪声支持度来估计该序列是否频繁。
本文的工作更类似于PFS2算法,但PFS2算法在序列重构时将所有候选序列等同看待,而本文则提出了区分不同候选序列重要程度的算法,并提出一种阈值修正策略来提高挖掘结果的准确度。
2 问题定义
2.1 差分隐私
差分隐私保护可以保证对数据集的查询处理结果对于具体某个记录的变化是不敏感的,即在数据集中添加或删除一条数据记录不会对查询的输出结果产生显著影响。因此,即使在最坏情况下,攻击者获得除目标记录外的所有记录信息,仍可以保证这一记录的敏感信息不会被泄露。
如果两个数据集D和D′相差最多为一个记录,则称D和D′为邻居数据集(NeighboringDatasets)。本文使用符号D~D′表示两个数据集是邻居关系。
定义1ε-差分隐私[2]。给定两个邻居数据集D和D′以及一个随机算法A,Range(A)表示A的取值范围。若对于在数据集D和D′上的所有输出结果O(O∈Range(A)),算法A满足下列不等式,则称算法A满足ε-差分隐私。
Pr(A(D)∈O)≤exp(ε)Pr(A(D′)∈O)
(1)
其中,参数ε叫作隐私预算,控制着隐私保护的水平。ε越小,表示隐私保护水平越高。差分隐私的含义在于,对于算法的任一可能的输出结果而言,无论函数的输入是数据集D还是D′,得到这一输出的概率相差很小。
设计差分隐私算法的常用技术是向查询或者分析结果中添加噪声使数据失真。添加干扰噪声的大小与查询函数的敏感度密切相关。查询函数的敏感度是指改变数据集中任一记录对查询结果造成的最大改变量。
定义2 全局敏感度。设有函数f:D→Rd,输入为一数据集D,输出为一个d维实数向量。对于任意的邻居数据集D和D′,函数f的全局敏感度为:

(2)
其中‖·‖1表示L1距离。注意:函数的全局敏感度独立于数据集,仅由函数本身决定。不同的函数会有不同的敏感度。常用的计数查询的敏感度为1。
拉普拉斯机制是2006年由Dwork等[13]提出的一种实现差分隐私保护的方法。该机制的形式化描述如下:给定一个函数f:D→Rd,若一个随机算法A的输出结果满足等式(3),则A满足ε-差分隐私。
A(D)=f(D)+Lap(Δf/ε)d
(3)
Laplace机制适用于响应函数的返回值为实数型的情况,其主要思想是在真实的输出值上添加符合拉普拉斯分布的噪声以达到保护效果。添加的噪声量大小与Δf成正比,与ε成反比。对于函数返回值为整数的情况,Ghosh等[14]提出了拉普拉斯机制的特例——几何机制。该机制添加的噪声大小服从概率密度函数为式(4)的双边几何分布。本文方法也使用几何机制对频繁序列的支持度添加噪声。
Pr(δ=x)~exp(-ε|x|)
(4)
定理1 几何机制。设f:D→Rd是一个输出为整数、敏感度为Δf的函数。若一个随机算法A的输出结果满足等式(5),则A满足ε-差分隐私。
A(D)=f(D)+G(ε/Δf)d
(5)
通常,一个复杂的隐私保护问题通常需要多次运用差分隐私保护算法才能得以解决。在这种情形下,为了保证整个过程满足ε-差分隐私,需要合理地将全部预算分配到各个子过程中。这时经常利用差分隐私保护算法的一个很重要的性质——序列组合性。
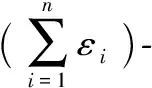
2.2 频繁序列模式挖掘
设字母表I={i1,i2,…,i|I|},一个序列S是字母表中一些项的有序排列。使用S=s1s2…s|S|表示一个长度为|S|的序列,也称为|S|-序列。一个序列数据库D是输入序列的集合,每个输入序列代表一个人的记录。
通常而言,模式是否频繁取决于模式的支持度与指定阈值的关系。基于这个事实,我们需要知道序列模式支持度的计算方法。在给出支持度的定义之前,先介绍序列的包含关系。
定义3 包含关系。给定两个序列S=s1s2…s|S|和T=t1t2…t|T|。如果存在整数w1 定义4 支持度。给定一个序列模式S和一个序列数据库D,在D中T的支持度定义为D中包含S的轨迹的数量。也就是说,Sup(T)=|{o|o∈D∧S⊆o}|。 频繁序列模式挖掘的任务就是在给定的序列数据库中找出所有支持度大于给定阈值σk的序列模式。然而,在挖掘频繁序列模式过程中存在隐私泄露的风险。基于这一事实,本文提出一种在保护个人敏感信息的前提下隐私地挖掘频繁序列模式的算法。下面先给出本文的问题定义。 问题定义:给定一个语义轨迹数据库D、隐私参数ε和一个阈值σk,本文的目标是设计DP-FSM算法来挖掘所有支持度大于σk的频繁序列模式,并计算每个频繁序列的支持度。该算法需满足如下要求:1)DP-FSM算法满足ε-差分隐私;2)DP-FSM算法具有较高的数据可用性。 为了使FSM满足差分隐私,最直接的方法是利用向下封闭属性[15]生成所有候选序列(即所有可能的频繁序列),并对每个候选序列的支持度添加扰动噪声,最后根据噪声支持度选出频繁序列。然而,这种方法结果效用性差。这是由于大量的候选序列会导致大量的扰动噪声,进而导致序列模式的噪声支持度主要取决于噪声,结果会造成严重失真。 3.1 算法描述 算法1 DP-FSM算法。 输入 序列数据库D,百分比η,阈值σk,隐私预算ε,字母表I; 输出 频繁序列及其噪声计数。 1) 〈l1,l2,…,ln〉=Estimate_Distribution(D,ε1) 3) lf=Estimate_Frequent_Maxlength(D,ε2,σk) //估计频繁序列的最大长度 4) FS=Mining_FrequentSequence(D,lmax,σk,ε3) //利用向下封闭属性[15]性质按序列长度递增的 //顺序挖掘所有长度小于lf的频繁序列; 5) 输出频繁序列模式及其噪声计数Perturb(FS,ε4)。 DP-FSM主要由预处理、挖掘和扰动三个阶段组成。 预处理阶段(算法1)~3)行):主要估计最大长度约束lmax和频繁序列的最大长度lf。 lf的计算方法如下:从1到lmax,计算i-序列的最大支持度,然后向其添加噪声G(ε2/log(lmax)),选出支持度大于阈值σk最大的整数i。 挖掘阶段(算法第4)行):算法按照序列长度递增的方式隐私地发现频繁序列 扰动阶段(算法第5)行):实现比较简单,向直接挑选出的频繁序列的支持度添加几何机制的噪声即可。 以下将着重介绍DP-FSM算法的核心——挖掘频繁序列阶段。 3.2 挖掘频繁序列模式 算法2DP-MiningFrequentSequence。 输入 频繁序列最大长度lf,截断序列长度约束lmax,隐私预算ε3,阈值σk; 输出 频繁序列集合FS。 1) For(k=1;k≤lf;k++) 2) Ifk==1 thenD′←D;Ck←I Else 3) Ck←Generate_CandidatSet(Sk-1); 4) D′=Truncate_Database(D,Ck,lmax) //截断数据库; 5) Sk←Choose_Candidate_Seed(D′,Ck,ε′,σk); 6) FSk=Discover_Frequent_Sequence(D′,Ck,ε′,σk); 7) FS=FS+FSk; 8) ReturnFS; 算法2描述了隐私地挖掘频繁序列模式的过程,其核心思想是利用候选序列在截断序列数据库D′中的噪声支持度判断该候选序列是否频繁。同时,为了提高挖掘结果的准确度,该算法从两个方面对阈值进行修正:1)截断序列数据库后会造成某些候选序列频率信息的损失,考虑到这种截断情况产生的误差(称之为截断误差),该算法修正判断阈值σk为σk-avg(θ′)+θ′,其中avg(θ′)为根据序列的噪声支持度θ′估计该序列在原数据库中的平均支持度。2)如果一个频繁序列模式被错误地标注为不频繁的模式,则它的任何超序列在不计算其支持度的情况下即被判定为不频繁的序列模式。考虑到这种情况产生的传播误差, 修正判断某一序列是否用于产生候选序列的阈值为σk-max(θ′)+θ′,其中max(θ′)为根据序列的噪声支持度θ′估计该序列在原数据库中的最大支持度。 1)截断序列数据库。这一步的目的是转换序列数据库使其满足长度约束。理想情况下,当收缩序列时,希望新得到的序列既满足长度约束又保存尽可能多的潜在频繁序列模式的频率信息。基于此,提出一种序列收缩的方法,通过无关项删除、连续模式压缩和智能序列重构三种策略收缩序列的长度。 a)无关项删除。 给定一个序列,当一个项不包含在任何候选序列中时,显然这个项对于候选集中任何序列模式的支持度无贡献。这样的项称为无关项,从序列中删除无关项不会导致任何频率损失。 基于向下封闭性质,如果一个项对于候选k-序列是无关项,那么对于长度大于k的候选序列也是无关项。 例1 设有序列A=abababebcdfg及候选2-序列集合{ab,bc,cd,ac},则efg为无关项,删除后为A1=abababbcd。 b)连续模式压缩。 一个序列可能包含一个连续出现的序列模式。对于k-序列的估计,可在不引起任何频率信息损失的情况下压缩连续的j个序列模式为连续的k个序列模式。这是由于在候选k-序列中的k个项最多来自k个模式。继续上面的例1,序列ab在A1中出现3次,则可用2个连续模式去代替它,即A2=ababbcd。 c)智能序列重构。 无关项删除和连续模式压缩在不导致频率(支持度)损失的情况下有效地收缩了序列。然而,在经过这两种方法处理轨迹序列后,某些序列仍然违背序列长度约束。直观地,收缩一个序列时仅需保留频繁序列的子序列,这是由于不频繁的子序列对频繁序列的支持度无贡献。然而,我们的目标是隐私地找到这些频繁的序列模式,为此提出一个启发式的方法预测某一个候选序列是否是频繁的。在实际生活中,如果一个候选序列的所有子序列是充分频繁的,那么该候选序列很可能是频繁的序列模式。基于这个观察,对每个候选i-序列(i≥2)分配一个频率分。 定义5 频率分。给定一个频繁(i-1)-序列的集合GS={S1,S2,…,Sd},一个i-序列X的频率分数为: (6) 其中,Si.sup′代表序列Si的噪声支持度。 但找到最优的lmax-序列这个问题是NP-hard的,为此提出一个贪心算法来收缩序列。贪心算法的思想如下:对于每条序列,迭代地添加包含在输入序列中高频率分数的候选序列,直到重构的序列达到最大集势。同时,我们注意到一个候选序列的频率分不应该是静态的:当一个候选序列的一些子序列已经添加到重构序列中后,为了使重构序列包含候选序列,该候选序列需要添加的子序列中项的数目少于其他候选序列。因此,在一个候选序列的一些子序列已经添加到重构序列后,应更新受影响的候选序列的频率分。 更新策略如下:假设一个候选序列Xi被添加到重构轨迹序列中,需更新集合X的频率分。对于每个剩余候选序列Xj⊂{X1,…,Xi-1,Xi+1,…,Xd},计算单个项的得分αj=fs(Xj)/i。假设已在重构序列中的最大子序列包含的项的数目为βj,则更新候选序列的频率分为fs(Xj)=fs(Xj)+αj*βj。 例2 继续上面的例1,同时假设候选序列的权重情况如下集合所示:{ab:8;bc:6;cd:4;ac:2};以及假设序列限制长度为4。经过无关项删除机制和连续模式压缩机制处理后,序列A由序列A2=ababbcd表示,但它的长度依然大于限制长度4,因此需要根据智能序列重构机制处理。依据该规则,首先选取ab加入到结果序列t′中去,然后更新候选序列bc的权重为6+1×8/2=10。cd的权重保持不变,ac的权重更新为2+1×2/2=3。则将bc添加到事务t′中,此时t′=abc,长度仍小于约束长度4。再按同样的方法进行下一次迭代,得到t′=abcd。此时t′的长度已达到了序列限制长度,因此,用序列abcd表示原序列A=abababebcdfg。 2)阈值修正。为了弥补截断误差和传播误差导致的频率信息的损失,受“双重标准”机制[10]的启发,提出一种新的支持度预估方法。该方法根据序列在转换后事务数据库中的噪声支持度估算序列在原始数据集中真实支持度信息,进而使用平均支持度来判断该序列是否频繁,使用最大支持度决定该序列是否会被用来生成候选序列。具体地来说,新的支持度预估方法主要由以下两步组成。 第一步:给定序列X的噪声支持度θ′,估算序列X在转换后数据集中的真实支持度θreal。根据“双重标准”中给定的定理可以得出: Pr(θreal|θ′)≈e-ε(θreal-θ′) (7) 第二步:根据序列在转换后数据集中真实支持度θreal,进一步估计序列在原始数据集中的真实支持度θ。这里通过分析随机截取方法产生的信息损失来衡量截断序列数据库方法产生的信息损失量。直观地,给定一个长度为l的序列记录t,若将t截取为t′序列记录,如果t中不包含序列S,则t′事务中也必然不包含序列S。因此只需要利用包含序列S的截断序列记录来计算其支持度。给定长度为l的序列记录,将长度为|t|包含i-序列S的事务t截取为t′序列记录,截取为t′序列记录包含i-序列S的概率为: (8) 将序列S在转换后数据集中的支持度看为随机变量,则该变量的期望是: (9) 与“双重标准”中计算最大支持度和平均支持度的方法相似,给定序列在转换后数据集中的支持度θreal,则序列在原始数据库的平均支持度: (10) 序列在原始数据库的最大支持度: max(θ″)= (11) 结合第一步和第二步的结论,给定序列在转换后数据集中的噪声支持度θ′,我们估算该序列在原始数据集中平均支持度为: (12) 最大支持度为: (13) 综上,在挖掘频繁序列模式过程中利用i-序列S的平均支持度来判断该序列是否频繁,利用最大支持度来决定该序列是否会被用来生成候选(i+1)-序列。换句话说,我们在判断是否频繁时将阈值σk修正为σk-avg(θ′)+θ′;在判断某序列是否用于生成候选序列时阈值σk修正为σk-max(θ′)+θ′。 以下首先对DP-FSM算法各阶段的隐私性能进行分析,然后利用差分隐私的序列组合性(性质1)给出整个算法的隐私性能结果。 预处理阶段: 对于序列数据库的集势|D|的计算,由于添加(删除)一个输入序列只影响|D|变化1,则这个计算的敏感度为1。因此,在计算时添加几何噪声G(ε11)满足ε11-差分隐私。相似地,计算aj的敏感度为1,添加G(ε12)也满足ε12-差分隐私。因此,根据差分隐私的序列组合性,计算lmax满足ε1差分隐私。对于lf的计算,当估计每个i-序列的最大噪声支持度时向其加入符合G(ε2/log(lmax))的噪声,文献[2]已给出证明,表明该过程符合ε2-差分隐私。 扰动阶段:扰动阶段的主要目标是向挑选出的频繁序列集合FS的真实支持度中添加噪声达到隐私保护的目的。此时,增加或者删除一条序列最多影响|FS|个频繁序列的支持度变化1,则计算频繁序列集合FS的支持度计数的敏感度为ΔFS=|FS|。因此,向FS的支持度计数添加G(ε4/ΔFS)满足ε4-差分隐私。 定理2 DP-FSM算法满足ε-差分隐私,其中ε=ε1+ε2+ε3+ε4。 证明 可以根据差分隐私的序列组合性(性质1)直接得出结论。 以下通过实验来评估DP-FSM算法的性能,实验环境为CPUInterCorei7-2600,频率3.40GHz,8GB内存,500GB硬盘,Windows7操作系统,所有的代码用C++编程语言实现。实验中将DP-FSM与目前最先进的隐私地挖掘频繁序列的算法PFS2进行比较。由于算法涉及到随机化,算法各运行15次后取平均值作为结果发布。 5.1 实验设置 实验中使用两个真实序列数据集:BIBLE[16]和MSNBC(http://kdd.ics.uci.edu/databases/msnbc/msnbc.html),数据集的参数设置如表1所示。 表1 实验数据集参数 (14) (15) 5.2 实验结果 5.2.1DP-FSM和PFS2算法的性能比较 图1(a)分析了在数据集MSNBC上阈值参数σk对FNR的影响。需要注意的是,实验中的阈值是指相对于整个数据集大小的比例。从实验结果可以看出,随着阈值参数σk的增大,PFS2算法的FNR呈现增大的趋势,这意味着随着σk的增大,PFS2算法挖掘结果的准确度降低,算法性能变差;而DP-FSM算法的FNR总体上呈现相对稳定的趋势。除此之外,从实验结果上看,就FNR而言,DP-FSM算法的性能总体上优于PFS2算法的性能。 上述实验结果是合理的。原因如下:阈值σk的增大意味着用于判断序列是否频繁的支持度变大,这样使得更多的序列变为非频繁的序列。PFS2算法在重构序列时未考虑候选序列频繁程度的差异性,很有可能导致频繁序列在截断序列数据库时未被保留,进一步导致根据噪声支持度错误地判断该候选序列为非频繁的序列模式。而DP-FSM算法由于在截断序列数据库时考虑了候选序列的差异性,有效地减小了误差。 图1(b)分析了在数据集MSNBC上阈值参数σk对两个算法的RSE的影响。从实验结果可以看出,随着σk的增大,DP-FSM算法的RSE变化不大,而PFS2算法的RSE也呈现增大的趋势。这种现象是由于随着σk的增大,对频繁序列设置的阈值要求更高。PFS2由于在重构序列时未考虑候选序列的差异性,导致结果集中含有大量的非频繁序列;又由于非频繁序列的支持度较低,故根据式(15),可得出随着σk的增大,PFS2算法的RSE增大。 图1 数据集MSNBC上算法的可用性 图2是算法DP-FSM和PFS2在数据集BIBLE上的性能结果。从中可以看出,这两个算法在该数据集的性能总体趋势与在数据集MSNBC上大体相似。 图2 数据集BIBLE上算法的可用性 5.2.2 阈值修正策略对DP-FSM算法性能的影响 为研究阈值修正策略对DP-FSM算法准确度的影响,将不带阈值修正策略的挖掘频繁序列模式的算法称为DP-RS。图3分析了阈值修正策略随着σk的变化对算法性能的影响。从中可以看出,带阈值修正的DP-FSM算法的性能优于不带阈值修正策略的DP-RS算法,并且随着阈值参数σk的增大,两个算法的性能差异性越大。因为阈值修正策略减少了挖掘频繁序列过程中的截断误差与传播误差,故相对于DP-RS算法,DP-FSM算法的准确度较高。又由于随着σk的增大,对频繁序列的要求更为严格,DP-RS算法由于误差的存在导致结果集中存在许多非频繁模式,从而导致FNR增大;并且大多非频繁模式的支持度较低,故DP-RS算法的RSE也较大。 图3 阈值修正策略对算法可用性的影响 本文首次针对频繁序列模式挖掘过程中的隐私泄露问题,提出了一种满足ε-差分隐私的算法DP-FSM。该算法首先从候选集中挖掘所有频繁序列模式,然后采用几何机制对挑选出来的模式的支持度添加几何噪声扰动。除此之外,为了提高挖掘结果的可用性,本文提出了一个阈值修正策略来减小挖掘过程中的截断误差和传播误差。最后,通过实验验证了该算法在满足差分隐私的前提下可获得较高的数据可用性。在未来的工作中,我们将研究如何合理地分配隐私预算使得挖掘结果的准确度达到最高值。 ) [1]SWEENEYL.k-Anonymity: a model for protecting privacy [J].International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 2002, 10(5): 557-570. [2] DWORK C.Differential privacy: a survey of results [C]// TAMC 2008: Proceedings of the 5th International Conference on Theory and Applications of Models of Computation, LNCS 4978.Berlin: Springer-Verlag, 2006: 1-19. [3] CHEN R, FUNG B C M, DESAI B C, et al.Differentially private transit data publication: a case study on the montreal transportation system [C]// KDD ’12: Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York: ACM, 2012: 213-221. [4] CHEN R, ACS G, CASTELLUCCIA C.Differentially private sequential data publication via variable-lengthn-grams [C]// CCS ’12: Proceedings of the 7th ACM CCS Conference on Computer and Communications Security.New York: ACM, 2012: 638-649. [5] BONOMI L, XIONG L.A two-phase algorithm for mining sequential patterns with differential privacy [C]// CIKM ’13: Proceedings of the 22nd ACM International Conference on Conference on Information & Knowledge Management.New York: ACM, 2013: 269-278. [6] XU S, SU S, CHENG X, et al.Differentially private frequent sequence mining via sampling-based candidate pruning [C]// ICDE ’15: Proceedings of the 31st IEEE International Conference on Data Engineering.Washington, DC: IEEE Computer Society, 2015: 1035-1046. [7] BHASKAR R, LAXMAN S, SMITH A, et al.Discovering frequent patterns in sensitive data [C]// KDD ’10: Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York: ACM, 2010: 503-512. [8] LI N, QARDAJI W, SU D, et al.PrivBasis: frequent itemset mining with differential privacy [J].Proceedings of the VLDB Endowment, 2012, 5(11): 1340-1351. [9] 张啸剑,王淼,孟小峰.差分隐私保护下一种精确挖掘top-k频繁模式方法[J].计算机研究与发展,2014,51(1):104-114.(ZHANGXJ,WANGM,MENGXF.Anaccuratemethodforminingtop-kfrequent pattern under differential privacy [J].Journal of Computer Research and Development, 2014, 51(1): 104-114). [10] ZENG C, NAUGHTON J F, CAI J-Y.On differentially private frequent itemset mining [J].Proceedings of the VLDB Endowment, 2012, 6(1): 25-36. [11] CHEN R, MOHAMMED N, FUNG B C M, et al.Publishing set-valued data via differential privacy [C]// Proceedings of the VLDB Endowment, 2011, 4(11): 1087-1098. [12] LEE J, CLIFTONC W.Top-kfrequent itemsets via differentially private FP-trees [C]// KDD ’14: Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York: ACM, 2014: 930-940. [13] DWORK C, McSHERRY F, NISSIM K.Calibrating noise to sensitivity in private data analysis [C]// TCC 2006: Proceeding of the Third Theory of Cryptography Conferenc, LNCS 3876.Berlin: Springer-Verlag, 2006: 265-284. [14] GHOSH A, ROUGHGARDEN T, SUNDARARAJAN M.Universally utility-maximizing privacy mechanisms [C]// STOC ’09: Proceedings of the 41th ACM STOC Annual Symposium on Theory of Computing.New York: ACM, 2009: 351-360. [15] AGRAWAL R, SRIKANT R.Fast algorithms for mining association rules [C]// VLDB ’94: Proceedings of the 20th Conference of Very Large Data Bases.San Francisco, CA: Morgan Kaufmann Publishers, 1994: 487-499. [16] ZHANG C, HAN J, SHOU L, et al.Splitter: mining fine-grained sequential patterns in semantic trajectories [J].Proceedings of the VLDB Endowment, 2014, 7(9): 769-780. This work is partially supported by the National Natural Science Foundation of China (61033007, 61622202, 61572119), the National Program on Key Basic Research Project (973 Program) (2012CB316201), the Fundamental Research Funds for the Central Universities (N150402005). LI Yanhui, born in 1989, Ph.D.candidate.Her research interests include data privacy, data query processing. LIU Hao, born in 1991, M.S.candidate.His research interests include privacy preserving, data mining. YUAN Ye, born in 1981, Ph.D., professor.His research interests include cloud computing, big data management. WANG Guoren, born in 1966, Ph.D., professor.His research interests include uncertain data management, graph data management, crowdsourcing data management. Frequent sequence pattern mining with differential privacy LI Yanhui*, LIU Hao, YUAN Ye, WANG Guoren (SchoolofComputerScienceandEngineering,NortheasternUniversity,ShenyangLiaoning110819,China) Focusing on the issue that releasing frequent sequence patterns and the corresponding true supports may reveal the individuals’ privacy when the data set contains sensitive information, a Differential Private Frequent Sequence Mining (DP-FSM) algorithm was proposed.Downward closure property was used to generate a candidate set of sequence patterns, smart truncating based technique was used to sample frequent patterns in the candidate set, and geometric mechanism was utilized to perturb the true supports of each sampled pattern.In addition, to improve the usability of the results, a threshold modification method was proposed to reduce truncation error and propagation error in mining process.The theoretical analysis show that the proposed method isε-differentially private.The experimental results demonstrate that the proposed method has lower False Negative Rate (FNR) and Relative Support Error (RSE) than that of the comparison algorithm named PFS2, thus effectively improving the accuracy of mining results. frequent sequence mining; Differential Privacy (DP); privacy protection; geometric mechanism; data mining 2016- 08- 12; 2016- 09- 06。 基金项目:北京市自然科学基金资助项目(4131001, 4142023)。 房俊(1976—),男,江苏南京人,副研究员,博士,主要研究方向:云数据管理、海量时空数据管理; 李冬(1989—),男,湖南永州人,硕士研究生,主要研究方向:云数据管理; 郭会云(1992—),女,河南漯河人,硕士研究生,主要研究方向:分布式系统调度; 王嘉怡(1993—),女,北京人,硕士研究生,主要研究方向:海量时空数据管理。 1001- 9081(2017)02- 0311- 05 10.11772/j.issn.1001- 9081.2017.02.0311 TP311.13;TP A3 DP-FSM算法


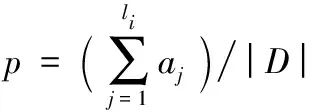


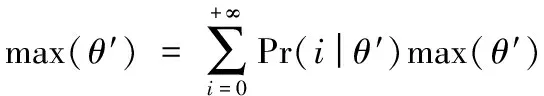
4 隐私性能分析
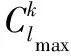
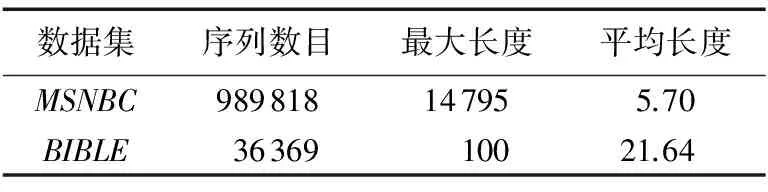
5 实验结果与分析
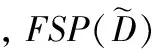






6 结语
