典型加筋板结构面内裂纹偏转与扩展行为分析

杨翔宁，许希武，郭树祥

(机械结构力学及控制国家重点实验室(南京航空航天大学), 南京210016)

典型加筋板结构面内裂纹偏转与扩展行为分析

杨翔宁，许希武，郭树祥

(机械结构力学及控制国家重点实验室(南京航空航天大学), 南京210016)

为研究筋条截面形式和多部位损伤对整体加筋板裂纹偏转行为和断裂特性的影响，采用断裂力学和有限元方法对其进行分析.首先建立整体加筋板疲劳裂纹扩展模型，通过与裂纹扩展速率试验进行比较验证模型可靠性；在此基础上讨论筋条截面形式对裂纹断裂参量和转折行为的影响；最后对多裂纹问题进行研究.结果表明：筋条截面形式对断裂参量的影响并不显著，裂纹偏转行为在远离筋条区域扩展时发生的可能性最大；多裂纹情况下裂纹并不会转折，而是笔直扩展进而连通成一条大裂纹，同时由于相邻裂尖的强烈干涉，造成应力强度因子剧增，加速裂纹扩展，进而严重缩短了扩展寿命，因此需采用有效的修补手段来提高结构的剩余强度和使用寿命.

整体加筋板；裂纹偏转；多裂纹损伤；断裂特性；疲劳寿命；有限元法

整体加筋板[1]作为现代飞机中的典型结构，具有结构质量轻、检测维修方便等优点，但其损伤容限能力却低于传统结构[2].为提高整体加筋板损伤容限能力，研究相应的裂纹止裂技术是工程中亟需解决的问题.针对这一问题，国内外学者进行过大量研究，普遍认为裂纹偏转止裂技术可以作为整体加筋板结构损伤容限设计中重要的止裂手段[3-6].Kosai等[7]基于有限元法成功模拟出加压圆柱形机身壁板上的裂纹转折轨迹；Chen[8]利用三维壳单元模拟分析波音舱板试验，引入裂纹转折理论预测得到的裂纹扩展路径与几乎试验测量路径一致；王生楠等[9]利用有限元法研究了整体机身壁板中纵向裂纹的转折现象与止裂特性.但这些研究主要考虑的是单一筋条参数和单裂纹情况，没有考虑筋条截面形式和多部位损伤对裂纹偏转行为和断裂参量的影响.

本文针对这一问题，采用线弹性断裂力学和有限元法，对整体加筋板的裂纹偏转行为和断裂特性进行研究，进一步讨论筋条截面形式对整体加筋板疲劳裂纹断裂特性的影响，并考虑多部位损伤情况下裂纹的扩展轨迹，分析了裂纹偏转止裂技术的可行性.

1 模型建立与验证

基于Llopart等[10]进行的试验，利用通用有限元计算分析软件Abaqus和专业裂纹分析软件Zencrack共同建立两桁条含中心裂纹的整体加筋板模型，有限元模型如图1所示.为提高计算效率，建模时对实际结构进行一定简化，包括边界条件和载荷的引入方式等方面.其中，壁板长310 mm，宽174 mm，桁条间距100 mm，初始裂纹长度5 mm.对整体加筋板两端施加x方向的疲劳拉伸载荷，同时为保证断裂模式为纯Ⅰ型模式，需对外壁板表面施加z方向的位移约束以起到抗弯作用.

图1 简易整体加筋板模型

其中，结构材料参数分别为：弹性模量(E)69.5 GPa，泊松比(μ)0.33，屈服强度(σs)350 MPa.

基于上述模型，当裂纹扩展至剪切带时，需要对图2中3个点处的型应力强度因子KI和T应力进行分析.其中点1处于内壁板表面，点2与点1间距0.5 mm，点3位于外壁板表面，与点1相距2.5 mm.

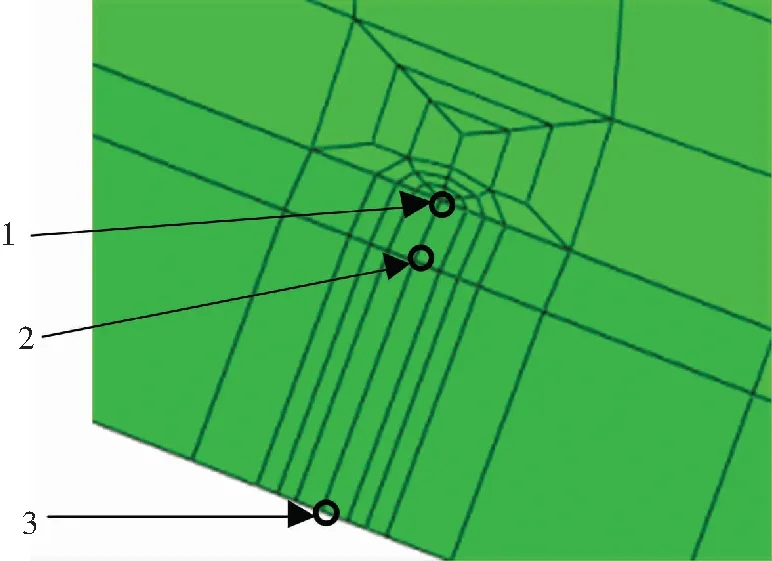
图2 KI和T应力计算点位置

当确定应力强度因子后，可采用Paris疲劳裂纹扩展公式预测整体加筋板中心裂纹扩展速率为

式中：da/dN为每一次循环的疲劳裂纹增长速率；ΔK=Kmax-Kmin为每一次循环中应力强度因子的变化幅值；C、n分别为材料常数.疲劳裂纹扩展参数如表1所示，其中:Kc为材料断裂韧性(板厚为2.5 mm时测得);σ0为最大拉伸载荷;R为应力比.该模型的裂纹扩展速率与试验数据对比如图3所示，由于试验中两个裂纹尖端扩展时具有非对称性，因此试验数据取两个裂纹尖端扩展速率的平均值.

表1 疲劳裂纹扩展参数

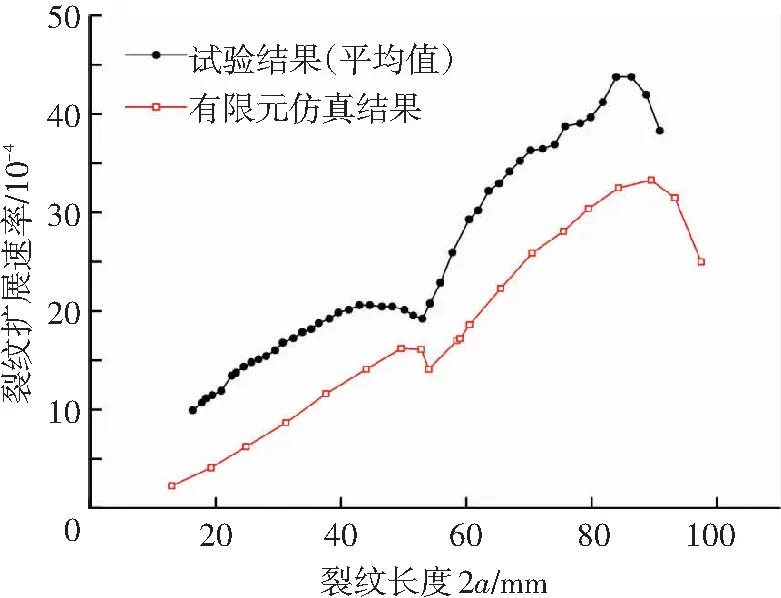
图3 仿真结果与试验结果的比较

从图3中可以看出，两条曲线的扩展趋势大致相同，验证了本文模型的可靠性.随着裂纹长度增加，裂纹扩展速率也逐渐加快，并在接近剪切带与筋条根部时有一定的降低.但是由于建模时没有考虑壁板与筋条间的倒角，也造成了仿真结果与试验结果间存在一定的误差，图中显示有限元仿真结果一直低于试验数值，说明其计算结果更趋于保守.另外，有限元分析结果表明两个裂纹尖端扩展速率相同，然而试验中两个裂纹尖端扩展时具有非对称性，其中一个裂纹尖端扩展速率较快，会首先扩展至筋条根部，造成裂纹扩展速率较早地衰减.

2 筋条截面形式的讨论

2.1 筋条截面形式对裂纹断裂参量的影响

基于上述建模分析方法，分析讨论筋条截面形式对疲劳裂纹断裂参量的影响.为更好地分析由于截面形式不同而产生的影响，将所有讨论的截面形式其截面积均保持一致.众所周知，不同的截面形式由于结构传力特性的不同，被应用在不同的位置.例如，刀型筋条，即上述模型中筋条形式，由于只能产生较小的惯性矩，因此结构效率不高.并且在单轴拉伸载荷作用下，其抵抗结构变形的能力不强.本文讨论了3种典型筋条形式对疲劳裂纹扩展的影响，分别为Z型、帽型和工字型，其筋条截面形式如图4所示.

为了分析讨论筋条截面形式对裂纹扩展的影响，首先需要找到一个基础形式进行参照.将刀型筋条形式下的模型作为基础形式，观察分析不同筋条截面形式下裂尖应力强度因子随裂纹长度的变化规律，如图5所示.

图4 不同筋条截面形式

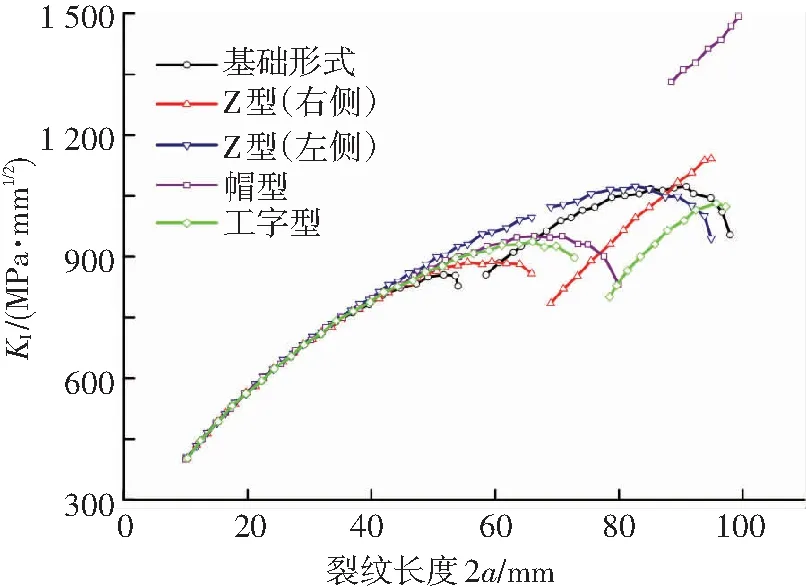
图5 不同筋条截面形式下的应力强度因子比较

计算应力强度因子时，由于厚度突变位置处没有从理论上进行定义，因此从图5中可以看到同一筋条形式下，应力强度因子变化过程会产生一段间隙.

Z型筋条是一种十分常见的筋条形式，它可以与壁板很好地胶接和铆接.在计算分析时考虑到筋条截面的非对称性，因此需要分别计算裂纹左右两个尖端的应力强度因子.从图5中可以看出，Z型筋条模式下应力强度因子随裂纹长度的变化规律与基础形式基本相同.当裂纹从左侧进行扩展时，可以发现应力强度因子数值首先与基本形式基本相同，但随着裂纹进一步扩展，其数值略高于基本形式.这是因为基本形式下，当裂纹长度接近60 mm时，壁板厚度与Z型筋条相比增加0.5 mm.当裂纹从筋条右侧进行扩展时，可以看出当裂纹扩展至筋条根部时，应力强度因子随之下降，但随着裂纹进一步扩展，筋条根部发生破坏后，由于结构大面积失效，势必造成应力的增大，应力强度因子将急剧上升，并最终超过基本形式下应力强度因子的最大值.

筋条截面为帽型时，筋条内部的应力强度因子同样需要计算.当裂纹长度扩展至80 mm时，将到达筋条根部.在此之前，应力强度因子的变化规律与基础形式基本相同，同样由于当裂纹扩展接近60 mm时，壁板厚度与基础形式相比减少0.5 mm，因此之后应力强度因子值略大于基础形式.当裂纹扩展至筋条内部，即筋条一边腹板被完全切断时，由于剩余强度大幅降低，因此应力强度因子将急剧上升.

工字型与基本形式截面属性大致相同，这种筋条形式是基本形式的衍生，可将它看作在基本形式的腹板上下两端分别增加一个缘条.与上述两种筋条形式相比，其应力强度因子的变化规律与基本形式相比有更好的一致性.不同的是由于上缘条的存在，当裂纹已经扩展至下缘条后，虽然结构截面大面积失效造成应力强度因子急剧上升，但由于上缘条并未发生损坏，因此其应力强度因子的最大值与基本形式相比仍降低了3.7%.

通过上述分析可知，3种常见筋条形式中，帽型筋条对裂纹扩展的抑制作用最差，尤其当裂纹扩展至筋条内部时，其应力强度因子的最大值与基本形式相比增加了近40%.与此相比，工字形筋条即使裂纹已经扩展至筋条下缘条，但由于上缘条未发生破坏，结构完整性得到了一定保证，因此应力强度因子与基础形式相比还有所下降，故而通过比较可得出工字形筋条的止裂性能最优.

综上所述，对于含中心小裂纹的整体加筋板结构，裂纹在远离筋条区域进行扩展时，筋条截面形式对断裂参量的影响是很小的.仅当裂纹扩展至剪切带附近时，应力强度因子才会略有降低或增加.

2.2 筋条截面形式对裂纹偏转行为的影响

考虑复合加载及多尺度屈服情况，裂纹扩展遵循最大切向应力准则[11].基于最大切向应力准则，Williams[12]率先提出二阶裂纹偏转理论，该理论潜在地表明了与试验观察结果的最佳拟合，但同时还要确定特征过渡区宽度rc和二阶应力分量T，其中rc为材料常数需要通过试验确定.该项理论认为，T应力数值为正，且rc>r0时，距离裂尖前方r0处的最大正切应力方向变为非零，即裂纹发生转折.r0的数值大小为

式中T为二阶应力分量.由上式可以看出，裂纹偏转主要取决于KI与T应力的比值.

为了分析不同筋条形式对裂纹偏转行为的影响，满足裂纹偏转的第1个条件，即T>0，需要对整体加筋板模型施加双轴疲劳拉伸载荷，其大小关系为σx=2σy.同时，考虑裂纹偏转的第2个条件，需要首先根据KI和T应力的比值计算r0，再与裂纹尖端的特征过渡区宽度rc比较大小.不同筋条形式下r0和rc的比较如图6所示.由于并没有具体的理论公式去计算裂纹尖端特征过渡区rc的大小，因此根据文献[13]采用的数值，本文的rc值取为1.5 mm.

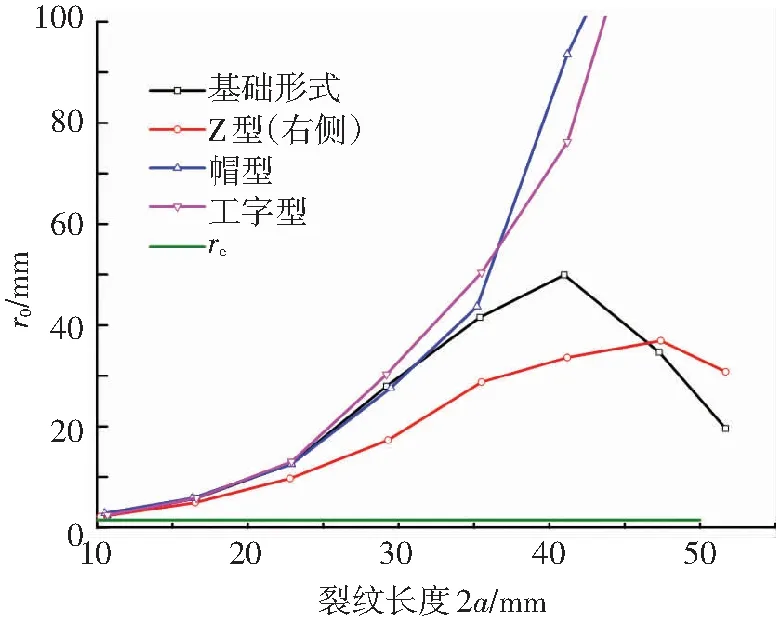
图6 不同筋条形式下r0和rc的比较

考虑裂纹偏转的两个条件，T>0和rc>r0.虽然已经对整体加筋板模型施加双轴拉伸疲劳载荷，满足了T>0的条件，但是从图6中不难发现，r0的值一直是大于裂尖特征过渡区宽度rc的，因此裂纹并未发生转折，这也与试验观察的结果一致.随着裂纹长度逐渐增加，r0的值也逐渐增加，因此裂纹扩展在远离筋条时发生转折的潜能是最大的.从图6中还可以看出，在基础形式和Z型筋条模式下，裂纹逐渐扩展至剪切带的过程中，由于剪切带的作用，造成T增大，K降低，因此K与T的比率随之减小，计算得出的r0也逐渐减小.但是与裂纹起始扩展时的r0相比，此时的r0还是远大于裂尖特征过渡区宽度rc的.并且由帽型和工字形筋条模式下r0随裂纹长度的变化规律中可以看出，这两种筋条形式并不利于裂纹的转折行为.

综上所述可知，裂纹偏转行为受筋条截面形式的影响并不明显.在不同筋条截面形式下，裂纹在远离筋条区域扩展时发生转折的可能性是最大的.

3 多裂纹问题

现行的损伤容限设计主要考虑的是根据长期使用经验确定的单一裂纹情况，没有考虑到多裂纹的存在.裂纹偏转作为一种整体加筋板结构潜在的有效止裂手段，将被用来探究其对含共线多裂纹整体加筋壁板结构破损安全特性的影响.

共线多裂纹整体加筋板模型建立如图7所示，以基础形式筋条下的单裂纹模型为基础，在中心裂纹两端分别增加1条与中心裂纹尺寸相等的裂纹.由于该模型具有对称性，因此只需分析其中3个裂纹尖端的断裂参量即可.

图7 多裂纹模型

为了分析多裂纹情况下裂纹的转折特性，同样对多裂纹整体加筋板模型施加双轴疲劳拉伸载荷，载荷数值及关系与单裂纹时一致.并且为了更准确地分析相邻裂纹尖端参数的变化规律，减少网格畸变带来的负面影响，需要对整体加筋板模型中心壁板布置较为密集的单元.由之前单裂纹情况下，裂纹偏转特性的研究可知，裂纹在远离筋条的区域扩展时裂纹的转折潜能最大，即裂纹在初始扩展时最易发生转折.利用Abaqus通过引入线载荷的辅助方法可得到裂纹在初始扩展时，不同裂纹总长(3条裂纹长度之和)下3个裂纹尖端的T应力数值，见表2.

从表2中可以看出，3个裂尖的T应力始终为负值，并且随着裂纹总长度的增加，负值的程度逐渐增大，说明相邻裂尖的干涉作用会降低T应力的数值.在线弹性材料中，T应力通常用于分析裂纹的稳定性和转折问题.当T<0时，裂纹将会沿着初始扩展方向直线扩展.因此在多裂纹情况下，不同位置的裂纹均不会发生转折.可见对于共线多裂纹整体加筋板的损伤容限设计，裂纹偏转并不是一个有效的止裂手段，需要采用另外的有效止裂技术进行破损安全设计.

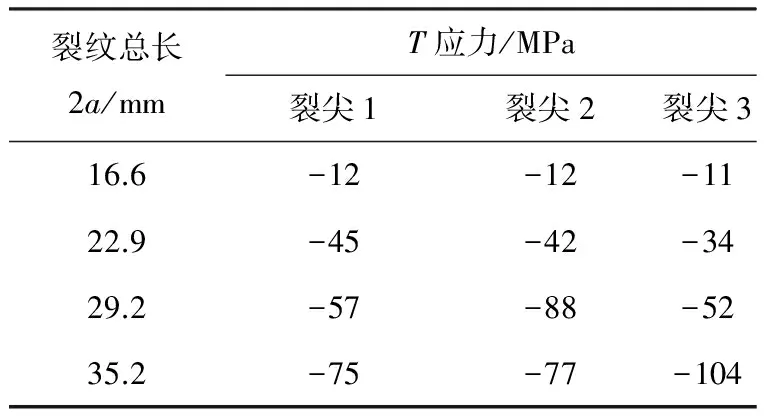
表2 裂纹尖端的T应力

由于多裂纹情况下裂纹均未发生转折，随着裂纹长度的逐渐增加，相邻裂纹尖端必然会发生连通.根据Swift[14]净截面屈服准则，当两条相邻裂纹尖端的残存韧带等于两裂尖塑形区尺寸之和时，两条裂纹发生连通而形成一条大裂纹.由于整体加筋壁板一般处于平面应力状态，裂纹塑性区尺寸的计算可采用平面应力状态下的计算公式：

式中σs为屈服强度.通过计算可知，当有限元分析进行到247步时，此时R1+R2+da1+da2=10 mm(裂纹间距)，即裂纹发生连通.在裂纹发生连通前，不同位置裂尖处的应力强度因子随裂纹扩展的变化如图8所示.

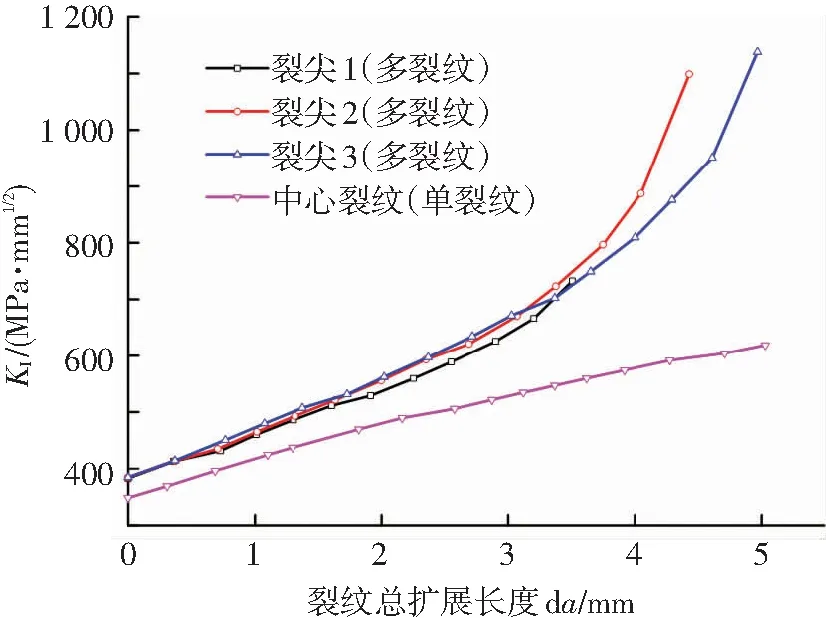
图8 裂纹连通前各裂尖应力强度因子变化

从图8中可以看出，3个裂尖应力强度因子随裂纹长度的变化规律大致相同，但由于筋条剪切带对裂纹扩展的抑制作用，使得不同位置处裂尖的总扩展长度不同，其关系为裂尖3>裂尖2>裂尖1，进而造成最终应力强度因子峰值的差异性.同时通过对比单裂纹和多裂纹情况下，相同位置处中心裂纹应力强度因子的变化规律可知，多裂纹时由于裂纹间的相互作用，使得应力强度因子数值始终高于单裂纹情况.尤其是在裂纹扩展后期会产生强烈的干涉而导致应力强度因子剧增.

由于裂尖强烈干涉而导致应力强度因子剧增，势必会加速裂纹扩展，进而缩短结构疲劳扩展寿命.多裂纹与单裂纹情况对结构疲劳寿命的影响如图9所示.

图9中多裂纹寿命曲线A、B两点之间的间隔表明，当裂纹扩展至37.8 mm时，裂纹发生连通，因此裂纹长度突变至41.5 mm.从图9中可以看出，裂纹的扩展速率随着裂纹长度的增加逐渐加快.同时在多裂纹情况下，总共历经了13 769次循环载荷，仅占单裂纹情况的41.6%，可见多裂纹损伤对整体加筋板结构的损伤程度远大于单裂纹情况.因此，对于多裂纹损伤结构，仅仅采用裂纹止裂手段是远远不够的，亟需采用有效的修补手段(如增加止裂带条[15])来提高结构的剩余强度和使用寿命.

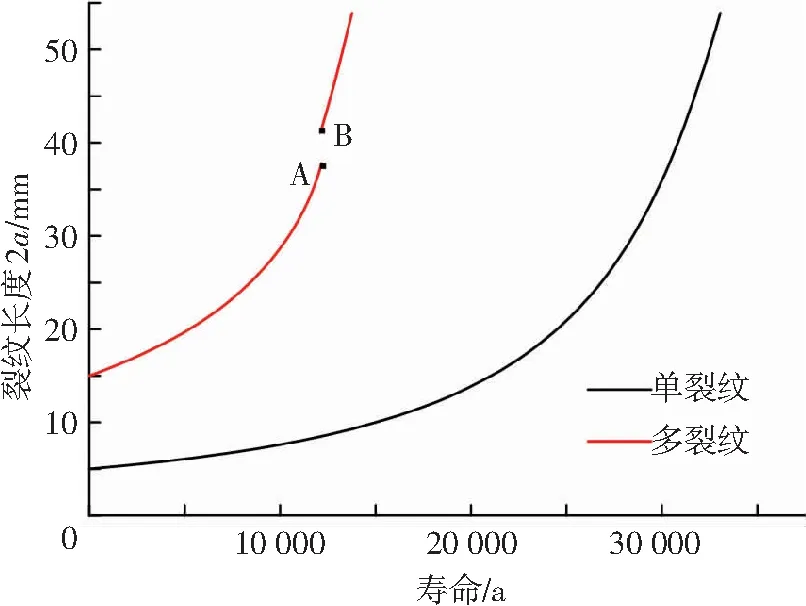
图9 寿命变化曲线

4 结 论

1)本文综合线弹性断裂力学和有限元方法，模拟分析了一个含中心裂纹两桁条整体加筋板结构的疲劳裂纹扩展过程，通过与试验数据的对比证明本文的建模方法是十分可靠的.

2)不同筋条截面形式对疲劳裂纹断裂参量的影响并不明显，仅当裂纹扩展至筋条附近时有一定的差异性；同时基于二阶裂纹偏转理论，发现不同筋条形式下裂纹发生转折行为的潜能大致相同，均为在裂纹扩展初期发生转折的可能性最大.

3)研究表明,多裂纹结构进行损伤容限设计时，不能将裂纹偏转作为一种有效的止裂手段.并且由于损伤程度严重，需要采用有效的修补手段来提高结构的剩余强度和使用寿命.

[1] 杨帆, 岳珠峰, 李磊. 基于弧长法的加筋板后屈曲特性分析及试验[J]. 应用力学学报, 2015, 32(1): 119-124. DOI: 10.11776/cjam.32.01.B119. YANG Fan, YUE Zhufeng, LI Lei. Analysis and experiment of post-buckling characteristics of stiffened panel under compress load by arc-length method[J]. Chinese Journal of Applied Mechanics, 2015, 32(1): 119-124. DOI: 10.11776/cjam.32.01.B119.

[2] SWIFT T. Damage tolerance in pressurized fuselages[C]//Proceedings of the 11th Plantema Memorial Lecture, New Materials and Fatigue Resistant Aircraft Design (ed. D L Simpson). Warley, UK: Engineering Materials Advisory Services Ltd, 1987:1-77.

[3] FOSSATI M, COLOMBO D, MANES A, et al. Numerical modeling of crack growth profiles in integral skin-stringer panels[J]. Engineering Fracture Mechanics, 2011, 78(7): 1341-1352. DOI: 10.1016/j.engfracmech.2011.03.005.

[4] PETTIT R G. Crack turning in integrally stiffened aircraft structures[D]. New York: Cornell University, 2000.

[5] 殷之平,郭今,黄其青. 基于材料各向异性的整体梁裂纹转折分析[J]. 西北工业大学学报, 2012, 30(2): 160-164. DOI: 10.3969/j.issn.1000-2758.2012.02.002. YIN Zhiping, GUO Jin, HUANG Qiqing. Analyzing crack turn of wing-beam integrated structure based on anisotropic mechanical properties of aluminum alloy[J]. Journal of Northwestern Polytechnical University, 2012, 30(2): 160-164. DOI: 10.3969/j.issn.1000-2758.2012.02.002.

[6] 殷之平,陈安,黄其青, 等. 整体翼梁止裂筋条对裂纹转折特性的影响分析[J]. 机械科学与技术, 2012,31(1): 59-62. DOI: 10.13433/j.cnki.1003-8728.2012.01.030. YIN Zhiping, CHEN An, HUANG Qiqing, et al. Analyzing effects of crack-arresting stringer of integrated wing beam structure on crack turning characteristics[J]. Mechanical Science and Technology for Aerospace Engineering, 2012, 31(1): 59-62. DOI: 10.13433/j.cnki.1003-8728.2012.01.030.

[7] KOSAI M, SHIMAMOTO A, YU C T, et al. Axial crack propagation and arrest in a pressurized cylinder: An experimental-numerical analysis[J]. Experimental Mechanics, 1999, 39(4): 256-264. DOI: 10.1007/BF02329802.

[8] CHEN C S. Crack growth simulation and residual strength prediction in thin shell structures[M]. Ithaca, New York: Cornell University, 1999.

[9] 王生楠, 张妮娜, 秦剑波. 整体机身结构纵向裂纹转折与止裂特性分析[J]. 西北工业大学学报, 2007, 25(4): 472-477. DOI: 10.3969/j.issn.1000-2758.2007.04.002. WANG Shengnan, ZHANG Nina, QIN Jianbo. Exploring engineering significance of turning of longitudinal crack in integral airframe structure[J]. Journal of Northwestern Polytechnical University， 2007, 25(4): 472-477. DOI: 10.3969/j.issn.1000-2758.2007.04.002.

[10]LLOPART L, KURZ B, WELLHAUSEN C, et al. Investigation of fatigue crack growth and crack turning on integral stiffened structures under mode I loading[J]. Engineering Fracture Mechanics, 2006, 73(15): 2139-2152. DOI: 10.1016/j.engfracmech.2006.04.005.

[11]COTTERELL B, RICE J R. Slightly curved or kinked cracks[J]. International Journal of Fracture, 1980, 16(2): 155-169. DOI: 10.1007/BF00012619.

[12]WILLIAMS M L. On the stress distribution at the base of a stationary crack[J]. Journal of Applied Mechanics-Transactions of the ASME, 1957, 24 (3): 109. DOI: 10.1115/1.3640470.

[13]张茂，董登科，弓云昭，等. 整体壁板结构裂纹转折研究综述[C]. 西安：第三届全球华人航空研讨会论文集，2005: 44-55.

[14]SWIFT T. Damage tolerance capability[J]. International Journal of Fatigue, 1994, 16 (1): 75-94. DOI: 10.1016/0142-1123(94)90446-4.

[15]黄祥龙. 止裂条带增强金属薄壁结构剩余强度研究[D]. 上海：上海交通大学, 2013. HUANG Xianglong. Residual strength analysis of metal thin-walled structures reinforced by bonded straps[D]. Shanghai: Shanghai Jiao Tong University, 2013.

(编辑 张 红)

Analysis of crack turning and fracture characteristics of a stiffened panel

YANG Xiangning, XU Xiwu, GUO Shuxiang

(State Key Laboratory of Mechanics and Control of Mechanics Structures (Nanjing University of Aeronautics and Astronautics), Nanjing 210016, China)

Using the fracture mechanics and finite element analysis theory, the effect of section types of the ribs and multiple-site damage on the crack turning behavior and fracture characteristics of the integral stiffened panel is investigated. First the crack growth model of the integral stiffened panel was established, and the reliability of the established model was proved in comparison with the test results of the crack growth rates. Based on the above model, the influence of section types of the ribs on the crack fracture parameters and crack turning was discussed. Finally the multiple cracks problem was investigated. The study showed that the effect of the sectional types of the ribs on the fracture parameters was not significant and the crack turning was more likely to occur when the crack was growing far away from the ribs. In the case of multiple cracks, cracks will not turn, but grow straightly and connect to form a large crack. Moreover, the strong interference of adjacent crack tips can lead to the severe increase of stress intensity factor and acceleration of the crack growth. Furthermore, the crack propagation life will be seriously shortened. Therefore, effective repairing methods are needed to improve the residual strength and service life of the structure.

integrally stiffened panel; crack turning; multiple crack damage; fracture characteristics; fatigue life; finite element method

10.11918/j.issn.0367-6234.201509088

2015-09-22

国家自然科学基金(11272146)

杨翔宁(1991—)，男,硕士; 许希武(1963—)，男，教授，博士生导师

许希武，xwxu@nuaa.edu.cn

V215.6

A

0367-6234(2017)04-0042-06