让数学具有“画面感”
——例说小学数学教学中运用几何直观的可能路径
2017-04-19章勤琼
◇章勤琼

一、几何直观的含义与作用
几何直观是《义务教育数学课程标准(2011年版)》(以下简称课标)中提出的十个核心概念之一:“几何直观主要是指利用图形描述和分析问题。”对此,孔凡哲教授和史宁中教授进一步把几何直观定义为“借助于见到的(或想象出来的)几何图形的形象关系,对数学的研究对象(空间形式和数量关系)进行直接感知、整体把握的能力”,并且认为“几何直观可以体现为实物直观、简约符号直观、图形直观、替代物直观四种表现形式”。[1]
事实上,对于数学教学工作者而言,相比几何直观“是什么”,对几何直观“能做什么”以及“可以怎么做”的探讨更有实践价值。因为“培养和发展学生的几何直观,需要依托数学课程的每个领域,依托具体的数学课程教学内容,需要具体落实在课程内容之中、课堂教学细节之中。”[1]下面本文将以北师大版第四版教材(以下简称北师大版教材)为例,谈谈在小学数学教学中运用几何直观的四种可能路径。
二、小学数学教学中运用几何直观的可能路径
几何直观应该在小学数学教学中发挥重要作用,这种作用可以体现在数学教学的不同领域与内容。比如,可以利用几何图形帮助理解数学概念、解决数学问题。注意这里的数学概念与数学问题不局限于几何问题,甚至更多时候是非几何的问题。笔者认为,在小学数学教学中有效运用几何直观可以有以下四种可能路径。
(一)用图形及其关系帮助学生理解数学概念。
小学数学中的有些概念对于小学生而言是比较难理解的。例如小数的认识,说到底小数的认识是对整数十进制系统的扩充。但对整数的十进制系统的认识可以借助小棒满十根捆成一捆这样的实物操作,帮助学生突破“满十进一”这一对位值制理解的难点。在对小数的认识中,同样需要为学生提供直观材料,丰富他们的理解经验。而图形是一种理想的素材。比如,北师大版教材四年级下册“小数的意义”中,通过图1将正方形看成“1”,然后分别通过十等分后涂色和一百等分后涂色的方式,帮助学生理解十分位、百分位的位值概念以及数位之间的进位关系。在图2中,则是通过图形感知小数中不同位值的大小关系并建立小数与图形之间的关联。

图1

图2
除直接利用图形外,还可以利用图形之间的关系,比如“小数的意义”(如图3)中对0.6和0.60进行比较,给出同样大小的表示“1”的两个正方形,其中一个涂上6个表示0.1的长方形,另一个涂上60个表示0.01的小正方形,容易发现涂色部分是一样多的,所以得出0.6=0.60。通过这样对比两个图形中涂色部分后再解释“小数的末尾添上‘0’或去掉‘0’,小数的大小不变”,相比脱离图形直接说明,学生更好理解。
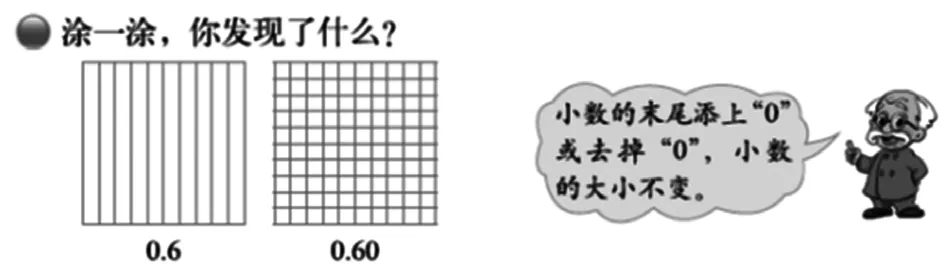
图3
(二)用图形与几何的形式描述、表征和解决数学问题。
有些数学问题可以用图形的方式进行表征。比如,在北师大版教材四年级上册“乘法分配律”这一内容中(如图4),计算墙壁上瓷砖的数量时,可以直观地看出有两种不同的计算方法。更进一步地,从图5中可以明显看出长方形ABCD面积的两种不同计算方法。在这里,图形直观地表征出了乘法分配律,两种计算方法不同,但结果一样。
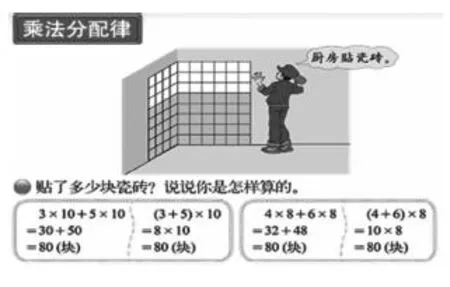
图4

图5
当然,几何直观最重要的一个作用是利用图形解决数学问题,这是指在解决或说明数学问题时,不用任何的文字或公式,只需要用图形展示就可以。美国的《数学杂志》曾经开设专栏“无需语言的证明(Proof Without Words)”,收集了很多这样的例子。譬如要计算,只需要给出图6,不需要更多文字的说明,就可看出这个算式跟代表1的大正方形相比,少了最后一个空白的小正方形,也就是最后一次分割后剩下的,所以结果应为

图6

图7
(三)理解数学时建立起直观与画面感。
在小学数学教学中,教师需要思考小学生是以怎样的一种方式学习和理解数学的。如果学生能以更加直观和更有画面感的方式理解所学的数学,相比以文字或公式的方式,会有更好的效果。
如在教学负数和分数时,需要让学生体会数系扩充的两条重要路径:一是以前学习的正数系统在数轴上是往一边生长的,而学习了负数之后,数的系统就可以同时往两边生长;二是以前学习的整数系统是跳跃的、离散的,而在学习了分数之后,数的系统就变得连续、稠密了。
北师大版教材四年级上册“负数的认识”中,除生活中的负数外,还需要跟正数对应起来学习负数,让学生体会以跟正数“对称”的方式来认识负数,并能认识到0作为“对称轴”的特殊性。
在北师大版教材五年级上册“分数的意义”中,采用了图8的“分数墙”。通过填写分数墙,学生能直观地感受到引入分数之后数的稠密性。不管多么小的分数,在它和0之间总还存在着更小的分数。而且通过对、…这样持续分割的过程,也可以让学生感受无限接近0却永远到不了0的极限思想。

图8
通过几何直观,可以帮助学生建立画面感,有助于他们更深刻地理解数学。
(四)充分考虑学生的直观感受。
运用几何直观在小学数学教学中还有一个非常重要的值得思考的路径,即在数学教学时充分考虑学生的直观感受。比如,在教学三角形分类时,直接将三角形分为钝角三角形、直角三角形和锐角三角形,对小学生而言可能是比较困难的。因为从学生的直观认知来看,他们对钝角三角形和锐角三角形的分辨是困难的。因此,在教学中可以考虑先将最特别的直角三角形区别出来,再将直角三角形作为分水岭,来分辨钝角三角形和锐角三角形[2](如图9)。
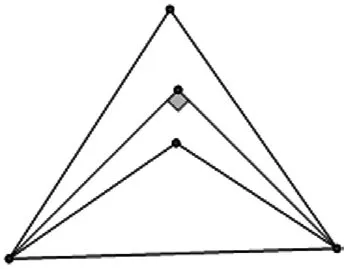
图9
综上所述,在小学数学教学中,可以从多种不同的路径来运用几何直观,充分发挥图形与几何的直观作用,帮助学生更好地理解数学。当然,还有一些相关的重要概念需要厘清,如“几何直观”“直观几何”“几何中的直观”等。不过,对于小学数学教师来说,相比真正弄清几何直观的含义,能够认识到几何直观在小学数学教学中的价值,并知道怎样运用到教学中,可能更有现实意义。正如莎士比亚所言:“玫瑰不叫玫瑰,芳香依然如故。”
参考文献:
[1]孔凡哲,史宁中.关于几何直观的含义与表现形式——对《义务教育数学课程标准(2011年版)》的一点认识[J].课程·教材·教法,2012,32(7):92-97.
[2]史宁中.基本概念与运算法则——小学数学教学中的核心问题[M].北京:高等教育出版社,2013.
