太阳定标基准星轨道仿真设计研究

谭伟 陈轩 齐文雯 何红艳

(北京空间机电研究所，北京 100094)



太阳定标基准星轨道仿真设计研究

谭伟 陈轩 齐文雯 何红艳

(北京空间机电研究所，北京 100094)

遥感卫星辐射定标是提高遥感数据辐射质量、监测遥感卫星性能变化的重要途径。首先简要介绍了遥感卫星绝对辐射定标原理，讨论了现行遥感卫星绝对辐射定标方法及其优缺点，在此基础上提出了一种基于太阳定标基准星的在轨辐射定标方法，并对太阳定标基准星的轨道设计方法进行了研究。文章针对高分二号(GF-2)卫星的轨道特点设计了满足其遥感相机定标要求的太阳定标基准星轨道模型，据此分析GF-2卫星和太阳定标基准星的轨道关系，得到遥感相机对太阳定标基准星的可见时长，验证了此辐射定标方法的理论可行性，其计算和分析结果对提高今后我国遥感卫星辐射定标精度具有参考意义。

遥感卫星；绝对辐射定标；太阳定标基准星；轨道仿真

1 引言

在遥感数据应用初期，通常采用遥感影像判读解译的方式实现对地表资源情况的定性描述，对遥感器的辐射定标精度要求并不高。随着资源、海洋、气象、环境与灾害监视领域对全球环境动态监测要求的不断提高，传统判读方法已不能满足遥感信息应用要求，以定量化遥感数据为基础，确定环境要素参数的需求日益增多，进一步提高遥感数据定量化应用精度的要求日益迫切，而定量化应用的前提是高精度的绝对辐射定标，因此遥感器辐射定标的重要性逐渐受到广泛共识，对辐射定标精度的要求也随之明确[1]。

现行的在轨绝对定标方法包括星上漫反射板定标、场地定标及与其他卫星交叉定标[2]，这几种方法各有优缺点，其中星上漫反射板定标法是通过搭载一块光学性能稳定的漫反射板，在星上通过可覆盖全视场的漫反射板对遥感相机进行定标，其优点在于定标过程与大气路径无关，精度较高，缺点是设计和工程实现难度大，且增加了载荷质量，目前国内遥感相机几乎不采用该方法；场地定标法是利用地物均匀、反射率变化较小的地面场(如戈壁、湖面等)作为定标场对相机进行定标，并通过地面实测参数进行定标精度检验，其优点是原理方法较为简单，相对可实现性高，缺点是对成像区域的地物特征和大气条件具有严格的要求，需要大量同步观测数据，投入的人力、物力等资源较大；交叉定标是以辐射定标精度较高的遥感器作为参考对目标遥感器进行定标，其优点是资源投入较少，不需要严格的实测数据，缺点是目标遥感器与参考遥感器需严格的匹配时间、空间、光谱、成像条件等[3-4]，定标精度的约束因素多。国产遥感卫星目前采用的在轨绝对辐射定标方法，如场地定标、交叉定标等，受成像大气路径等因素的影响，其定标精度已达到了理论极限值，很难再有进一步的提高。目前国产卫星的绝对辐射定标精度与国外还有一定差距，如红外光定标精度徘徊在1～1.5 K，可见光通道定标精度约5%～7%，而国际水平则分别可达到0.2 K和2%[5]。

本文基于国内外研究成果，结合遥感卫星辐射传输过程，从原理设计、建模方面进行分析，针对在轨辐射定标方法，分析太阳定标基准星和遥感卫星的空间状态和轨道特征，得到二者的空间关联关系，结合计算和仿真结果验证了基于太阳定标基准星辐射定标的理论可行性。

2 基于太阳定标基准星辐射定标的原理和设计

2.1 在轨绝对辐射定标原理

遥感卫星对景物成像时，一般地面景物的辐射特性作为相机的输入，用目标反射率或辐亮度表征，相机的输出为遥感图像，以数字计数值(digital number，DN)作为表征形式，绝对辐射定标是建立探测器输出信号与遥感相机输入辐射量之间关系的过程[6]。一般而言，绝对辐射定标的主要目标是确定相机入瞳处的辐亮度与探测器输出信号之间的函数关系，即确定绝对定标系数。定标原理可表述为[7]

(1)

式中：L为辐亮度，单位为W·m-2·sr-1·μm-1；G为定标斜率，单位为W·m-2·sr-1·μm-1；Dn为遥感图像数字计数值，无单位；B为定标截距，单位为W·m-2·sr-1·μm-1。

太阳定标基准星定义为一颗或多颗位于特定轨道的卫星，搭载具有稳定光学性能的漫反射板，通过反射太阳光，对太阳光的辐射能进行衰减，将合适强度的太阳辐射能量间接引入在轨光学遥感器，以太阳辐射作为定标源对遥感相机进行定标。整个标定过程中，太阳辐射作为基准定标源，其传递链路主要由3部分组成：太阳向基准星的直射过程、基准星反射太阳光的过程和遥感器接收基准星反射能量的过程。太阳辐射能量传递过程如图1所示。

基于基准星的在轨绝对辐射定标避免了地面场景、大气等不确定因素对成像的影响，主要影响其定标精度的因素，包括到达基准星表面的太阳辐照度的测量不确定度、基准星与遥感器入瞳处之间的距离测量不确定度、基准角的测量不确定度、基准星表面材料及制造工艺的不确定度等，这些因素的不确定度均较小，可将定标精度大大提高。

2.2 满足辐射定标要求的太阳定标基准星轨道分析

在上述介绍的基础上，本文将重点对太阳定标基准星的轨道设计过程进行计算和仿真。采用太阳定标基准星进行在轨绝对辐射定标时，为实现最佳光路、孔径定标及与太阳光谱分布最佳匹配，主要有以下约束因素。

(1)基准星与待定标遥感卫星的距离。考虑搭载及设计要求，基准星搭载的漫反射板面积满足定标孔径需求时，遥感器对漫反射板的成像空间分辨率有一定的限制，进而约束了基准星与待定标遥感器之间的距离。

(2)基准星受光照范围。定标时，基准星所搭载的漫反射板通过反射太阳光，进行适当衰减后将太阳辐射间接引入待定标遥感器。太阳光与漫反射板及漫反射板与待定标遥感器视轴的夹角(即光线在漫反射板的入射角和反射角)均影响辐亮度，当衰减后的太阳光满足定标对辐亮度的要求时，才能完成定标。因此，定标过程只能在基准星的太阳光照区域内进行，且对太阳光与漫反射板及漫反射板与遥感器视轴夹角均有一定限制。

(3)杂散光。地球和大气反射光等杂散光是影响定标精度的重要不确定因素，在轨定标时，通过卫星的姿态指向变化，基准星处于遥感器地球视场之外时，此时探测器接收到的辐射与地球和大气反射光无关，是理想的定标区域。

其中，约束因素(1)与两卫星的相对位置有重要关系，它们的相对距离是决定是否能够实现定标的关键。本文中结合卫星的轨道参数，建立卫星在地心坐标系中的实时坐标，确定两卫星之间的相对位置关系，进而计算太阳定标基准星相对待定标卫星的有效定标时段。

已知轨道六根数：半长轴a、偏心率e、近地点幅角ω、升交点赤经Ω、轨道倾角i、真近点角θ。通过轨道六根数可求解卫星在近焦点坐标系的中的速度矢量v和位置矢量r，具体计算过程如下。

参考GJB1028—1990，首先建立地心(第二)轨道坐标系(本文称为“近点坐标系”)和地心(第一)赤道坐标系(本文称为“地心赤道坐标系”)，如图2所示，图中Ω为升交点赤经，i为轨道倾角，ω为近地点幅角。近点坐标系：坐标原点O为地心；Ox轴在卫星轨道面内，指向近地点方向；Oz轴指向卫星轨道平面正法向方向；O-xyz为右手直角坐标系。地心赤道坐标系：坐标原点O为地心；OX轴在赤道面内，指向春分点；OZ轴垂直于赤道平面，与地球自转角速度矢量方向一致；O-XYZ为右手直角坐标系。

在近点坐标系中，卫星的状态由位置和速度来描述。

(2)

(3)

由地心赤道坐标系到近焦点坐标系需要3次旋转完成，旋转顺序为“313”。

第一次绕Z轴旋转角度Ω，至O-X′Y′Z′坐标系。正交变换矩阵为

(4)

第二次绕X′轴旋转角度i，至O-X″Y″Z″坐标系。正交变换矩阵为

(5)

第三次绕Z″轴旋转角度ω，至O-xyz坐标系。正交变换矩阵为

(6)

最后，将上述3个旋转矩阵相乘，便得到地心赤道坐标系至近地点坐标系的正交矩阵为

(7)

由于这是一个正交矩阵，所以它的逆矩阵即是由近焦点坐标系到赤道地心坐标系的变换矩阵Q′，即Q′=Q-1。

式(2)和式(3)为卫星在近焦点坐标系中的状态向量，则通过与变换矩阵Q′相乘，便可得到卫星在赤道地心坐标系中的状态向量为

(8)

因此，对于基准星和待定标遥感卫星，当给定其轨道六根数后，可分别求出其在地心坐标系中的初始状态向量，包括初始位置向量r0和速度向量v0。卫星经历Δt时间间隔后，两卫星的状态向量(即位置向量和速度向量)可由如下方法计算得到。

(9)

(10)

式中：Δt为卫星飞行时间间隔；χ为轨道全局近点角，由下述全局开普勒方程迭代解出[9-10]。

(11)

式中：α为轨道半长轴的倒数；S(z)和C(z)为斯达姆夫函数。

(12)

式中：z=αχ2；sinh和cosh分别表示双曲正弦和双曲余弦运算。假设基准星初始状态为(r1，v1)待定标卫星初始状态为(r2，v2)，经历Δt时间间隔后，两卫星状态向量分别为(r1′，v1′)和(r2′，v2′),得到两卫星的相对距离为

ΔS=|r1′-r2′|

(13)

在STK仿真软件中，可设置两卫星之间最大和最小的距离约束、太阳定标基准星的光照约束来获取它们互相之间的可视时长。而地球视场约束则需根据STK软件输出的时间文件，借助MATLAB软件可在STK软件输出的时间段内计算基准星和待定标卫星在地心赤道坐标系中的位置向量r1′和r2′，它们之间的夹角β可由空间余弦定理得到，如式(14)所示。当β大于与待定标卫星视场相关的临界角时，此时基准星处于待定标卫星的地球视场之外，对应的时间段为有效的可定标时段。

(14)

3 基准星轨道分析验证

3.1 基准星与典型遥感卫星轨道关系设计

一般待定标的目标遥感器均为运行在太阳同步轨道的高分辨率对地观测卫星，例如以中国第一颗亚米级商业遥感卫星高分二号(GF-2)为待定标遥感器，设计满足其定标需求的基准星轨道。GF-2卫星轨道与遥感器主要参数如表1所示。

表1 GF-2卫星参数Table 1 Parameters of GF-2 satellite

1)考虑两卫星之间的距离约束

考虑到卫星搭载的可行性，现假定太阳定标基准星搭载的漫反射板大小为2 m×2 m，且对漫反射板成像时相机视轴方向始终能保持垂直于漫反射板。研究表明当目标对遥感器的角分辨率大于10个像素时，方可作为有效定标源[11-12]，即要求遥感器对漫反射板的空间分辨率最大不超过2 m/10，即0.2 m。结合GF-2卫星待定标遥感器光学系统参数，由式(15)可得到基准星与GF-2卫星之间的最大距离。

(15)

式中：d0为GF-2卫星CCD探测器的像元尺寸，d0=10 μm；fl为高分二号卫星相机焦距，fl=7.785 m；GSD为空间分辨率，且GSD≤0.2 m；D为两卫星之间的距离，在满足GSD=0.2 m的条件下，可得到两卫星之间的最大距离为Dmax=155.7km。

2)地球视场杂散光的影响

基准星满足与GF-2卫星的距离要求且在其地球视场之外，此时无地球视场杂散光的影响。通过卫星姿态机动来实现相机视轴的大角度变换。为了仿真计算时边界约束的需要，可假定遥感器视场在地球之外时即无大气杂散光的影响(目前国内遥感卫星的姿态机动能力足够保证遥感器完全指向在地球之外来避免大气向上散射的影响)，因此如图3所示，当GF-2卫星视场与地球相切时，此时为卫星地球视场的临界条件。

图3中，R为地球半径，H为GF-2卫星轨道高度，当GF-2卫星视场与地球边缘相切时为临界视场，根据余弦定理可求得临界角β=65.5°。

考虑上述距离约束，此时地球静止轨道、大椭圆轨道均不适合作为太阳定标基准星的轨道；基准星轨道为低于GF-2卫星的太阳同步轨道时，当遥感卫星与太阳定标基准星的夹角不小于临界角β时，才能消除地球杂散光的影响，而基准星轨道高于GF-2卫星时，此时不受地球杂散光的约束。图4为基准星轨道高度低于GF-2卫星的情形。

图4中，R′为基准星轨道半径，H′为基准星和GF-2卫星的轨道高度差，Dmax为两卫星最大距离155.7km，β为GF-2卫星地球视场临界角，根据GF-2轨道高度、两卫星最大距离Dmax和临界角β，利用余弦定理得到R′=6 938.9 km。此轨道半径为受GF-2卫星轨道距离和视场约束的最小值，而理论最大轨道半径则为GF-2轨道半径加上距离约束155.7km。

3.2 理论计算和仿真试验分析

本文中将基于STK对不同参数的太阳同步轨道进行仿真，主要仿真参数为轨道半径与轨道倾角，轨道半径范围为6960～7100km，轨道倾角GF-2卫星轨道倾角(97.96°)附近的95°～100°，其他轨道参数同于GF-2卫星。

STK中太阳定标基准星与GF-2卫星轨道示意图如图5所示，Sun表示太阳的方位，JZSat表示太阳定标基准星，GF-2表示待定标的高分二号卫星。

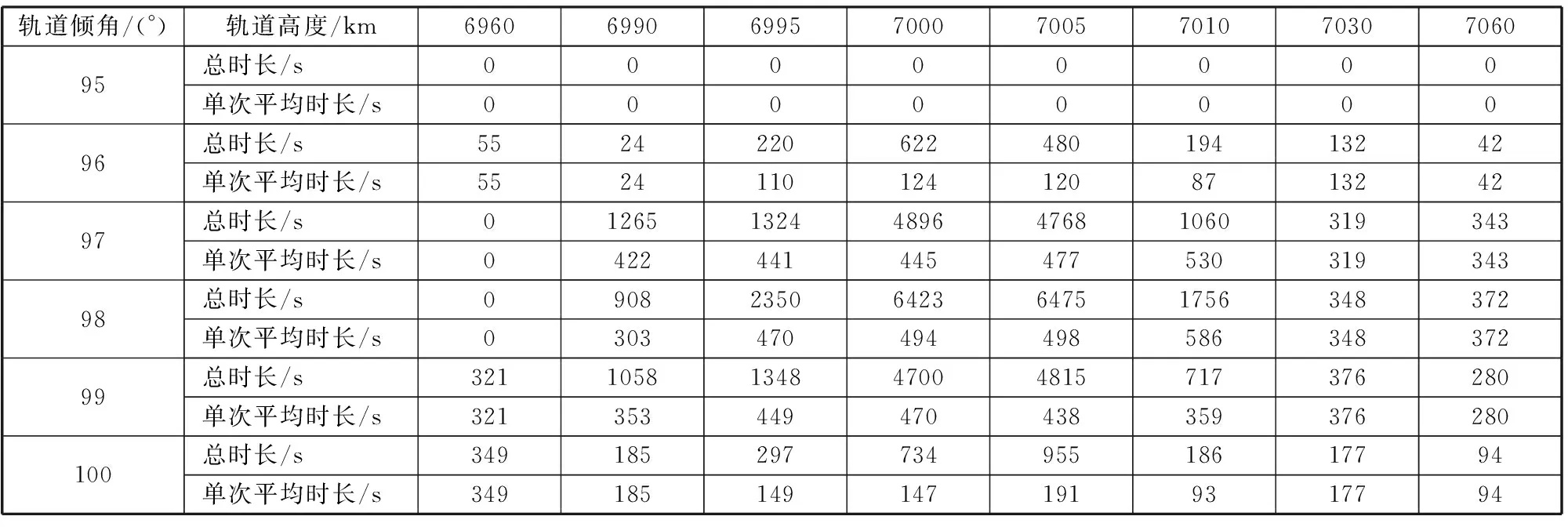
通过STK的轨道Access功能可计算不同轨道上卫星的可视时间。考虑两卫星的距离约束、受光照约束及地球杂散光的影响，计算GF-2卫星在一个重访周期内对JZSat的可视时间，仅考虑轨道高度和轨道倾角的变化，其中JZSat轨道高度由6960km逐渐变化到7100km，轨道倾角由95°逐渐变化到100°，得到GF-2卫星对JZSat的可视时长，部分计算结果如表2所示。

轨道倾角/(°)轨道高度/km6960699069957000700570107030706095总时长/s00000000单次平均时长/s0000000096总时长/s552422062248019413242单次平均时长/s5524110124120871324297总时长/s012651324489647681060319343单次平均时长/s042244144547753031934398总时长/s09082350642364751756348372单次平均时长/s030347049449858634837299总时长/s3211058134847004815717376280单次平均时长/s321353449470438359376280100总时长/s34918529773495518617794单次平均时长/s3491851491471919317794

在分别特定轨道半径和轨道倾角情况下，分析总时长和单次平均时长随另一参数的变化情况，以典型值为例进行绘图分析，结果如图6和图7所示，其中图6为轨道倾角为98.5°时可见时长与轨道半径的关系，图7为轨道半径为7004 km时可见时长与轨道倾角的关系。

从表2和图6、图7可以看出，基准星轨道高度和轨道倾角与GF-2卫星接近时，一个回访周期内GF-2卫星对基准星的总可视时长和单次可视时长均较大，且变化趋势表明：随着基准星轨道倾角和轨道高度与待定标遥感卫星逐渐接近，双星的可见时长也越来越长。实际工程中，遥感卫星对目标成像时间仅需数秒到数分钟，足够保障这个时段内完成遥感卫星对基准星进行成像，完成在轨辐射定标，当满足辐射定标所需的光照强度、成像孔径等要求时，此方法可突破地物特征和大气状况对绝对辐射定标精度的影响，提高辐射定标精度。

3.3 结果分析与讨论

根据上述验证结果可知：太阳定标基准星的轨道设置受限于与待定标遥感卫星的距离和角度约束以及基准星的光照约束，基准星置于太阳同步轨道，且遥感卫星具有较强的姿态机动能力时，才能有效完成在轨辐射定标。完成辐射定标需考虑遥感器入瞳光强、覆盖孔径的要求，满足遥感器入瞳光强需考虑基准星与遥感卫星之间由于距离变化导致遥感卫星接收到太阳光强的变化情况，光强随距离的增加而衰减；满足覆盖孔径则要求遥感卫星与基准星的距离小于某个与遥感卫星参数相关的临界值，如3.2节中计算得到GF-2卫星与基准星定标的临界距离为155.7 km，距离大于临界值时覆盖孔径过小，遥感器探测器上接受的光强不足以支持完成辐射定标。在后续研究中，还应综合考虑其他轨道根数对定标结果的影响。

本文提出的定标方法优点在于：突破了大气、地物等不确定性因素对在轨绝对辐射定标精度的影响，可对到达遥感器焦面的太阳辐射进行精确溯源，完成从太阳—基准星—探测器的辐射链路标定，最终通过对特性参数已知的漫反射板成像进而实现高精度定标。而此方法的缺点其主要局限包括：在轨定标时要求遥感卫星能够准确指向到基准星以保证覆盖遥感器视场的需要，对遥感卫星的姿态机动要求高，这种姿态精度将制约定标精度；基准星携带的定标漫反射板的性能在空间环境中需保持稳定，且具有均一的反射性能，其在轨性能退化应高度可控，否则将引入不确定性因素；考虑高分辨率遥感卫星一般为近地太阳同步轨道，基准星轨道也局限于几百千米到1000 km高的太阳同步轨道，对椭圆轨道或地球静止轨道的遥感卫星很难适用。

4 结束语

由于解决遥感卫星高精度辐射定标的难度较大，影响精度的不确定性众多，国内遥感卫星常规定标方法的辐射定标精度已很难突破。本文提出的基于太阳辐射定标基准星的在轨辐射方法，具有较为成熟的理论支撑，且在接下来一段时间内具备工程实现的技术可能性。以GF-2卫星为示例遥感卫星，根据理论计算与轨道关系验证结果表明：当基准星轨道高度和轨道倾角与GF-2卫星相近时，在GF-2回归周期内总可见时长和单次可见时长均较大，可满足进行辐射定标的时间要求。本文结合轨道关系从理论上验证了一种新的遥感卫星在轨辐射定标方法，研究得到的仿真结果和结论可为遥感卫星高精度在轨定标提供理论参考，对今后提高我国遥感卫星辐射精度，实现常态化定标工作具有一定的参考作用。

References)

[1] 朱军，吴雁林，沈中，等. 环境-1A、B卫星CCD相机系统级辐射定标数据分析[J]. 航天器工程，2009,18(5):73-79

Zhu Jun，Wu Yanlin， Shen Zhong，et al. Analysis of system-level radiometric calibration data for HJ-1A/B wide coverage camera[J]. Spacecraft Engineering，2009,18(5):73-79 (in Chinese)

[2]陈福春，陈桂林. FY-2C发射前后可见光星上定标的比较[J]. 量子电子学报，2007，24(6): 709-713

Chen Fuchun，Chen Guilin. Comparison between pre-launch and in-orbit visible onboard calibrations[J].Chinese Journal of Quantum Electronics，2007, 24(6): 709-713 (in Chinese)

[3]郑小兵. 高精度卫星光学遥感器辐射定标技术[J]. 航天返回与遥感，2011, 32(5): 36-43

Zheng Xiaobing. High-accuracy radiometric calibration of satellite optical remote sensors[J]. Spacecraft Recovery & Remote Sensing，2011, 32(5): 36-43 (in Chinese)

[4]Delwart S,Bourg L. Radiometric calibration of MERIS[C]// Proceedings of SPIE Conference on Sensors, Systems, and next-Generation Satellites XV, Paris: University of Paris, 2009, 7474:1-12

[5]顾行发，田国良，余涛，等. 航天光学遥感器辐射定标原理与方法[M]. 北京：科学出版社，2013: 72-126

Gu Xingfa，Tian Guoliang，Yu Tao，et al. Radiometric calibration theory and method of space optical sensors[M]. Beijing: Science Press，2013: 72-126 (in Chinese)

[6]顾明澧. 星载传感器在飞行时的绝对辐射定标方法[J]. 航天返回与遥感，2000, 21(1): 16-21

Gu Mingli. In-flight absolute radiometric calibration of satellite remote sensor[J]. Spacecraft Recovery & Remote Sensing，2000, 21(1): 16-21 (in Chinese)

[7]韩启金，张学文，乔志远，等.高分一号卫星PMS相机多场地宽动态辐射定标[J]. 红外与激光工程，2015, 44(1): 127-133

Han Qijin，Zhang Xuewen，Qiao Zhiyuan，et al. Wide dynamic radiometric calibration of GF-1 PMS sensors using multi-test sites[J]. Infrared and Laser Engineering，2015，44(1): 127-133 (in Chinese)

[8]Bond V R,Allman M C. Modern astrodynamics: fundamentals and perturbation methods[M]. Princeton: Princeton University Press, 1996: 227-230

[9]Battin R H. An introduction to the mathematics and methods of astrodymatics, revised edition[M]. New York: American Institute of Aeronautics and Astronautisc Inc, 1987: 198-205

[10] Prussing J E,Conway B A. Orbital mechanics[M]. New York：Oxford University Press, 1993

[11]Hugh H K, James M A, Kris J B. Radiometric calibration of spacecraft using small lunar images[C]// Proceedings of SPIE Conference of Environment Remote Sensing, Denver: University of Denver, 1999: 193-205

[12]Kieffer H, Jarecke P, Pearlman J. Initial lunar calibration observations by the EO-1 hyperion imaging spectrometer[C]// SPIE’s 16thAnnual International Symposium on Aerospace/Defense Sensing, Simulation, and Controls. Gainesville: University of Florida, 2002: 247-258

(编辑：张小琳)

Research on Orbit Simiulation Design of Sun-based Calibration Criterion Satellite

TAN Wei CHEN Xuan QI Wenwen HE Hongyan

(Beijing Institute of Space Mechanics & Electricity, Beijing 100094，China)

The radiometric calibration of remote sensing satellite is an important way to improve radiometric quality of remote sensing data, and to monitor the radiometric performance of satellite. On the basis of introducing radiometric calibration of remote sensing satellite and discussing the advantage and disadvantage of currently absolute radiometric calibration methods to be used, a new on-orbit radiometric calibration method based on solar radiometric criterion satellite is pre-sented. Then researches on orbit analysis and simulation is done to design a sun-based calibration criterion satellite orbit suited the calibration request of GF-2. According to the simulation above, the orbit relation of GF-2 and sun-based calibration criterion satellite is analyzed to get the access time between them. From the simulation the access time validates the theoretical possibility of radiometric calibration method proposed. The results can be meaningful in future for improving the radiometric calibration precision of domestic remote sensing satellite.

remote sensing satellite；absolute radiometric calibration；sun-based calibration crite-rion satellite；orbit simulation

2016-09-07；

2017-01-10

谭伟，男，硕士，研究方向为遥感数据处理与应用。Email：blacktanphay@126.com。

V529.1

A

10.3969/j.issn.1673-8748.2017.01.004