基于观测几何方法的星间链路天线转动总寿命需求分析
2017-04-19庄建楼何善宝宋铮周静
庄建楼 何善宝 宋铮 周静
(北京空间飞行器总体设计部,北京 100094)
基于观测几何方法的星间链路天线转动总寿命需求分析
庄建楼 何善宝 宋铮 周静
(北京空间飞行器总体设计部,北京 100094)
星间链路机械可移波束天线的转动总寿命需求是进行天线设计的重要依据。文章提出了一种基于观测几何的仿真方法,实现了航天器运动、航天器姿态控制、天线双轴转动相结合的仿真,同时避免了复杂的动力学仿真,并以某Walker-δ星座星间链路机械可移波束天线为例进行了分析,得出了较为准确的天线双轴转动总寿命需求,可用于长寿命高可靠性设计、制定具体的寿命试验方案等。该方法也适用于其他类型星座或其他依靠机械双轴实现指向跟踪的星间链路终端设备。
观测几何;星间链路;机械可移波束天线;总寿命;双轴;天线指向机构;万向节驱动组件
1 引言
当前,航天器星间链路机械可移波束天线(以下简称天线)已广泛用于在各类航天器之间建立持久的通信或测量链路,这类天线具有双轴的天线指向机构(Antenna Positioning Mechanism,APM)或万向节驱动组件(Gimbal Drive Assembly,GDA),简称双轴,双轴由正交的主动轴和从动轴(简称A轴和B轴)组成,每个轴包含空间驱动组件、微波旋转关节或高频电缆、低频电缆等活动部件。双轴在建立链路期间处于连续转动模式,双轴的长寿命高可靠性是确保航天器任务的关键因素,而其转动总寿命需求又是重要的设计约束条件,可用于双轴的具体设计、控制寿命试验的周期和成本。所谓总寿命,是指在规定条件下,产品从开始使用到报废的寿命单位数[1]。对于星间链路机械可移波束天线的双轴,表征其转动总寿命的一个重要的规定条件是转动速度,寿命单位数一般是累计转动行程(单位为转,1转指累计转动360°)和累计转动次数[2-3]。
人们普遍认识到了双轴长寿命高可靠性的重要性,但是对于转动总寿命需求的分析尚有不足。1996年,意大利阿莱尼亚航天(Alenia Spazio)V Costabile等人对意大利卫星-F2(ITALSAT-F2) L-Ka频段天线双轴进行了5×106个循环的寿命试验[4];2015年,中国空间技术研究院西安分院的田庆国对某型号星载机构类天线低频电缆进行了20万次折弯试验[5],但都不能说明试验量级所对应的实际总寿命需求。2012年,北京控制工程研究所刘继奎等人提出了星间链路天线驱动机构的长寿命设计和试验方案[6],但没有涉及与星间链路应用相关的总寿命需求;2015年,北华航天工业学院任华兴进行了某型号星间链路天线驱动组件轴系可靠性试验的研究[7],其中对于天线输出轴轴系应达到106转的转动总寿命需求缺乏论证。1977年,美国NASA的J Wu对陆地卫星-D(LANDSAT-D)TDRSS用户终端星间链路天线的谐波减速器进行了转动总寿命需求的计算[8],方法是使用本地卫星1轨道周期内的天线单轴平均转动行程乘以5年内的总轨道周期数,再乘以减速比,得到谐波减速器的转动总寿命需求,其中,平均转动行程为1次±90°的往复转动量(总计360°)。但经简单分析可知,该平均转动行程恰是天线在目标卫星处于本地卫星轨道面内、本地卫星无姿态变化情况下的典型转动行程,而实际上,目标卫星所处位置、本地卫星姿态都处在不断变化中,使用特定情况下的典型值作为平均值,必然造成较大的误差,使总寿命需求或者偏于保守,或者低于实际工程需要,甚至降低产品的可靠性或不能对产品进行充分的试验考核。航天器的运动、姿态控制是复杂的动力学问题,2013年北京航空航天大学陈蕾等人[9]实现了STK和Matlab/Simulink等多个商用软件相结合对航天器姿态控制的协同动力学仿真,但方法较为复杂。
根据以上问题,本文提出一种基于观测几何(即观测者、被观测目标之间的位置和角度关系)[10-11]的仿真方法,通过建立航天器和天线的观测几何模型,实现对航天器运动、航天器姿态控制、天线双轴转动相结合的仿真,既能得出较为准确的天线双轴转动总寿命需求,又能够避免复杂的多种软件协同的动力学仿真。
2 基于观测几何的仿真方法
航天器和天线的观测几何模型主要反映本地航天器和目标航天器之间的位置关系(一般以太阳、地球等天体为参照物来确定)、本地航天器的姿态控制所产生的坐标变换关系、天线双轴和本地航天器之间的坐标变换关系等,根据这些关系,可以计算出天线在指向目标航天器时的双轴转动角度。在离散的时间序列上重复上述计算,可以得出天线双轴的时间-转动角度序列,对该序列进行数值分析,即可得到关于天线单轴转动速度、累计转动行程、累计转动次数等转动总寿命需求参数。
一般地,航天器之间的距离足够远,使得航天器在惯性空间的绝对位置偏差对天线指向的影响可以忽略,在此前提下可进行以下合理的简化:
(1)把地球公转简化为匀速圆周运动,运动周期(即轨道周期)定义为质点通过圆周上同一点的时间间隔,这里的时间采用国际单位制秒为基础单位,地球轨道周期TY为1恒星年,近似为365.256 36个平太阳日,1平太阳日为86 400 s。
(2)当航天器的轨道近似为圆形时,其绕地心的运动也可以简化为匀速圆周运动。一般地,航天器运动由其轨道根数决定,即某一历元时刻的轨道半长轴a、偏心率e、倾角i、升交点赤经Ω、近地点辐角ω、平近点角M[12]。把航天器轨道简化为圆形,其轨道根数中:偏心率e=0,半长轴a等价于航天器轨道周期T,近地点辐角可取为ω=0,平近点角M就变成了相位角u。
(3)忽略地球和航天器轨道的摄动等因素,认为轨道面法向在惯性空间中的指向恒定不变。
下文以我国某型号Walker-δ星座[13]的星间链路机械可移波束天线为例,来具体说明如何采用基于观测几何的仿真方法进行转动总寿命需求分析。
3 星座和天线的观测几何模型
3.1 Walker-δ星座的建模
Walker-δ星座是一种全球覆盖最有效的星座类型,一般采用构型参数N/P/F/i来描述,其中,N为卫星总数,P为轨道数,F为相邻轨道面对应序号卫星之间的相位差因子,i即轨道根数之一的倾角。我国某型号Walker-δ星座的构型为24/3/2/55°。建立星座的观测几何模型所需的计算参数见表1。

表1 计算参数Table 1 Calculation Parameters
随着地球的周期性运动,阳光与卫星轨道面的夹角也呈现同周期变化,且在1个周期内必定出现1次太阳恰好位于卫星轨道面上并向轨道面正法向一侧运动的情况,记这个时刻为t0,此时轨道0的升交点赤经为Ω0。因轨道面均布,同一时刻轨道p(p∈[0,P-1])的升交点赤经为
(1)
轨道p第s颗卫星(s∈[0,N/P-1])记为卫星{p,s},其相位记为ups。易得出,任一卫星在任一时刻t的相位ups都可以用卫星{0,0}在t0时刻的相位u00(t0)来推知[13]:
(2)
本文通过一系列的坐标变换来模拟地球环绕太阳转动、卫星环绕地球转动、卫星偏航运动,得到卫星相对位置关系和姿态的动态变化。
日心坐标系、轨道面坐标系的关系是恒定的:
(3)
在任一时刻t,轨道坐标系与轨道面坐标系的坐标变换关系为(以下略去了时间变量t)
(4)
根据式(3)可得,轨道p和黄道面的夹角为arccos(cosεcosi+cosΩpsinεsini),该夹角越小,卫星可能发生的偏航角速度就越大,对天线双轴转动的影响就越大,因此取Ω0=0°,轨道0和黄道面具有最小夹角31.5°,代表了影响最大的情况。不失一般性,取u00(t0)=0°。
3.2 卫星偏航姿态控制
本文所述的卫星在飞行时需要进行偏航姿态控制,以确保太阳翼始终面向太阳。入射到卫星{p,s}处的阳光单位矢量b,变换到轨道坐标系后的坐标为
(5)
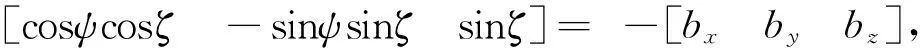
(6)
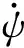
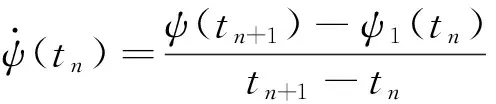
(7)
仍以ψ表示限速后的卫星实际偏航角,卫星偏航后的卫星姿态为
(8)
3.3 天线双轴的转动
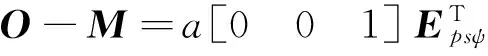
(9)
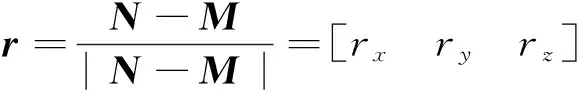
(10)
设天线的双轴布局形式为XY布局,即如图2所示,A轴沿卫星X轴摆放,且当天线指向地心时,B轴沿卫星Y轴摆放,此时天线指向和A轴、B轴都垂直。设天线A轴和B轴的转动角度分别记为α,β,那么当天线指向+Z上半空间的任意方向θ,φ时,双轴转角α,β为
(11)
4 总寿命需求的数值计算
星间链路包括同轨链路和异轨链路两种。在建立同轨链路时,目标卫星的视运动仅由本地卫星的偏航运动引起,在建立异轨链路时,目标卫星的视运动由本地卫星的偏航运动和目标卫星的相对位移共同引起,因此在建立异轨链路时,天线的转动总寿命需求必然大于建立同轨链路的情况。因此,本文仅对建立异轨链路的情况进行分析,并根据星间链路的拓扑设计[14-15],选取4条永久可见链路,本地卫星为卫星{0,0},目标卫星为{1,0}、{1,3}、{1,4}、{1,7},天线指向覆盖了θ接近 最大扫描角度70°的情况。
前述计算天线双轴转角的算法,过程繁琐,难以进行解析计算。只有借助数值计算的方法,每隔一定的时间计算双轴转角α,β,由此得出时间-双轴转角序列,采用差分、求和等方法,计算双轴的转速、累计转动量、转动次数。
乡村建设项目的特点为数量多且形式复杂,但总体技术难度不大,投资主体投资方式多样化,业主的需求也更加多样化。然而,项目总体规模偏小,管理成本占比反而增加。所以在初期阶段不能片面地追求经济效益,过分强调完成各类不合实际的指标。乡村EPC建造模式现阶段仍然是一种尝试,支出和回报不能成正比。乡村EPC建造模式的推进还需要进行探索实践,需要资金投入,不断总结经验,才能利用EPC自身优势在乡村振兴中发挥更大的作用。
4.1 双轴转动速度分析
天线双轴的转动速度,可以采用对时间的差分来计算。数值计算时,设时间为tn,双轴转动角度为αn,βn,那么双轴转动转速为
(12)
在1个卫星轨道周期内进行数值计算,以目标卫星{1,7}为例,图3显示了在1个卫星轨道周期内的天线双轴转动角度,图4显示了当本地卫星{0,0}的偏航角速度达到上限时,偏航角速度和双轴转动角速度的细节。
仿真的时间步长对转速分析精度影响很大,而如果采用秒级的步长,会使运算量非常大以至于难以进行全任务周期的分析。因此,本文采取了间接的分析方法,即把转速分解为两部分的叠加,第一部分是由星座内卫星之间的相对位置变化引起的,第二部分是由本地卫星的偏航运动引起的,实际转速的最大值不大于两部分转速最大值的算术和。对于第一部分,由于星座运行的周期性,可以在1个卫星轨道周期内进行小时间步长的精确分析,对于第二部分,由于本地卫星的偏航角速度有上限,可根据最大偏航角速度来计算分解到双轴上的最大转速。
在不计入卫星偏航的情况下,在1个卫星轨道周期内模拟卫星{0,0}与卫星{1,0}、{1,3}、{1,4}、{1,7}建链的情况,统计天线各轴的转速分布,结果如图5所示,可知各轴最大转速为不超过0.022 (°)/s,0.002 (°)/s的转速占比例最高,约占39%。
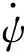
(13)
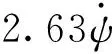
4.2 双轴累计转动行程和累计转动次数分析
双轴的累计转动行程为
(14)
双轴的累计转动次数,取决于如何界定“一次转动”,本文用简单的往复运动来类比,例如单摆的简谐运动,一次完整的往复运动包含了两次运动方向的改变,即一次从正向变为负向,一次从负向变为正向。因此,通过对天线双轴转动角度的数值分析,累计所有转动方向的改变次数即得出了转动次数。双轴在12年内的转动总寿命需求参数见表2。
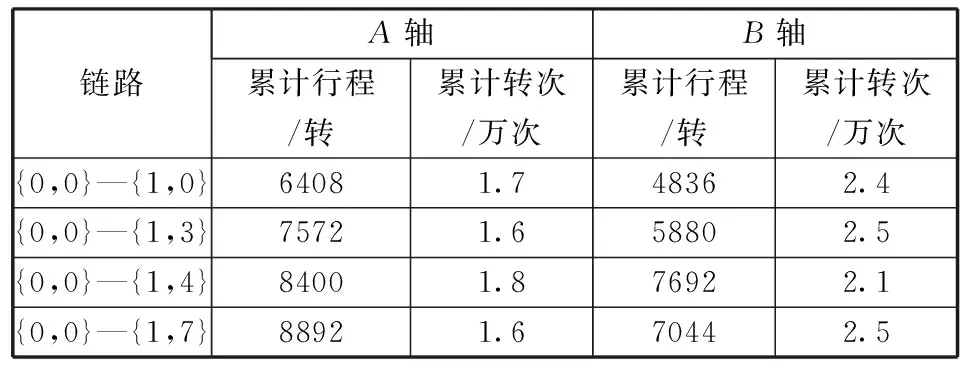
表2 12年转动总寿命需求Table 2 Turning total life requirement for 12 years
综上,通过对Walker-δ星座及天线的仿真及数值分析,得出了在建立永久可见链路的情况下,星间链路机械可移波束天线各轴的转动总寿命需求为:转动速度不超过0.42 (°)/s,12年累计转动行程不超过 0.9万转,累计转动次数不超过2.5万次。该转动总寿命需求是天线双轴长寿命高可靠性设计、制定具体的天线双轴的转动寿命考核试验方案的重要输入条件,实际的设计和试验还应在此基础上再保留一定的余量。
5 结论
基于本文上述研究,可得出以下结论:
(1)所提出的基于观测几何的仿真方法,得出了较为准确的天线双轴转动总寿命需求,与文献[8]方法相比,需求更客观,更适于指导工程实践;
(2)避免了对航天器运动和航天器姿态控制的多种软件协同的动力学仿真,更易于实施;
(3)虽然仅以我国某型号Walker-δ星座及天线为例进行了分析,但这种基于观测几何的仿真方法是普遍适用的,也适用于其他类型的星座,或其他类型的依靠机械双轴实现指向跟踪的星间链路终端设备。
References)
[1] 中国人民解放军总装备部.GJB 451A-2005 可靠性维修性保障性术语[S].北京:中国人民解放军总装备部军标出版发行部,2005:10
PLA General Armament.GJB 451A-2005 Reliability,maintainablility and supportability terms[S].Beijing:PLA General Armament Press,2005:10 (in Chinese)
[2]刘志全,李新立,遇今.长寿命航天器机构的加速寿命试验方法[J].中国空间科学技术,2008,28 (4):65-71
Liu Zhiquan,Li Xinli,Yu Jin.Methods of accelerated life tests for long-life spacecraft mechanisms[J]. Chinese Space Science and Technology,2008,28(4):65-71 (in Chinese)
[3]李新立,刘志全,遇今.航天器机构固体润滑球轴承的加速寿命试验方法[J].航天器工程,2008,17(5):82-87
Li Xinli,Liu Zhiquan,Yu Jin.A method of accelerated life test for solid-lubricated ball bearings of spacecraft mechanisms[J].Spacecraft Engineering,2008,17(5):82-87 (in Chinese)
[4]V Costabile,F Lumaca,P Marsili,et al.New antenna deployment,pointing and supporting mechanism[C]//Hampton VA United States: Langley Research Center,1996:65-76
[5]田庆国.星载机构类天线转动部位低频电缆布线方法研究[J].空间电子技术,2015,12(2):20-36
Tian Qinguo.The research of low-frequncy cables wiring method for the satellite institutional class antenna rotating parts[J].Space Electronic Technology,2015,12(2):20-36 (in Chinese)
[6]刘继奎,于国庆,崔赪旻,等.基于谐波传动的星间链路天线驱动机构设计研究[J].空间控制技术与应用,2012,38(4):57-62
Liu Jikui,Yu Guoqing,Cui Chengmin,et al. Design of harmonic drive-based gimbal drive assembly for ILA[J].Aerospace Control and Application,2012,38(4):57-62 (in Chinese)
[7]任华兴.导航星间链路驱动机构轴系组件可靠性试验研究[D].廊坊:北华航天工业学院,2015:11
Ren Huaxing.The research of reliability test on shafting components of cross-link drive mechanism for navigation satellite[D].Langfang:North China Institute of Aerospace Engineering,2015:11 (in Chinese)
[8]J Wu.Design study of TDRS antenna gimbal system for Landsat-D[M].Redondo Beach CA United States:TRW Defence and Space Systems Group,1977:24
[9]陈蕾,韩潮.基于Matlab/Simulink与STK的卫星姿态控制系统联合仿真研究[C]//2013全国计算机网络与通信学术会议.北京:中国电子学会,2013:103-108
Chen Lei,Han Chao.The study of co-simulation of satellite attitude control system based on Matlab/Simulink and STK[C]//National Academic Conference on Computer,Networks and Communication,2013. Beijing:The Chinese Institute of Electronics,2013:103-108 (in Chinese)
[10] 褚桂柏,马世俊.宇航技术概论[M].1版.北京:航空工业出版社,2002:111
Chu Guibai,Ma Shijun.An introduction to astronautics technology[M].1st ed.Beijing:Aviation Industry Press,2002:111 (in Chinese)
[11]赵春阳,赵怀慈,刘海峥.观测几何对目标探测性能影响的仿真分析[J].计算机仿真,2014,31(12):23-28
Zhao Chunyang,Zhao Huaici,Liu Haizheng.Simulation and analysis of effect of observation geometry on target detection performance[J]. Computer Simulation,2014,31(12):23-28 (in Chinese)
[12]Marcel J Sidi.航天器动力学与控制[M].杨保华,译.1版.北京:航空工业出版社,2011:20
Marcel J Sidi.Spacecraft dynamics and control[M].Yang Baohua, translated.1st ed.Beijing: Aviation Industry Press,2011:20 (in Chinese)
[13]张育林,范丽,张艳.卫星星座理论与设计[M].1版.北京:科学出版社,2008:39
Zhang Yulin,Fan Li,Zhang Yan.Theory and design of satellite constellations[M]. 1st ed.Beijing:Science Press,2008:39 (in Chinese)
[14]何善宝,李振东,刘崇华.星间网络拓扑的二分图及其关联矩阵表示法[J].航天器工程,2009,18(4):25-29
He Shanbao,Li Zhendong,Liu Chonghua. A method representing inter-satellite network topology with bipartite graph and its incidence martix[J]. Spacecraft Engineering,2009,18(4):25-29 (in Chinese)
[15]李振东,何善宝,刘崇华,等.一种导航星座星间链路拓扑设计方法[J].航天器工程,2011,20(3):32-37
Li Zhendong,He Shanbao,Liu Chonghua,et al. An toplogy design method of navigation satellite constellation inter-satellite links[J]. Spacecraft Engineering,2011,20(3):32-37 (in Chinese)
(编辑:李多)
Analysis of Turning Total Life Requirement for Cross-link Steerable Antenna Based on Observation Geometry Method
ZHUANG Jianlou HE Shanbao SONG Zheng ZHOU Jing
(Beijing Institute of Spacecraft System Engineering,Beijing 100094,China)
The turning total life requirement is very important for designing a cross-link steerable antenna. By introducing a simulation method based on observation geometry theory,the evolution of the constellation,the attitude controlling of satellites and the revolution of steerable antennas could be simulated without the complicated dynamical simulation. As an example,the method is applied to a Walker-δ constellation and its cross-link steerable antennas,and then the numerical analysis yields the turning total life requirement for antenna’s tow-axis.The method might be applied in designing for long life and high reliability,and for programming a life test. The method is universal for other types of constellations or other cross-link terminal devices which depend on steerable two-axis for target tracking.
observation geometry; cross-link; steerable antenna; total life; two-axis; APM; GDA
2016-09-09;
2016-11-18
国家重大科技专项工程
庄建楼,男,高级工程师,研究方向为航天器飞行器总体设计。Email:galaxyz@hotmail.com。
V443
A
10.3969/j.issn.1673-8748.2017.01.006
