基于高考试题的高中数学不等式教学研究

郭志宏

【摘要】在高中教育阶段，不等式知识是数学教学过程中的重点知识，也是一大难点知识，为使学生准确掌握、牢固记忆不等式知识，必须选择科学的、合理的、有效的教学方法.使学生在面对将不等式知识与三角、方程、函数等结合在一起的高考试题时，能够灵活运用不等式知识，准确地分析试题、解答试题.本篇论文中，笔者针对高考试题中的不等式知识，探讨高中数学不等式教学的相关有效措施.

【关键词】高考试题；高中数学；不等式教学

高考数学中，与不等式知识相关的试题相对来说比较多.基于这样的原因，高中数学教学过程中，必须加强对不等式知识的关注与重视，并要在不等式教学过程中运用科学的、合理的、有效的教学方法，以便提高教学效率与教学质量，使学生准确掌握、牢固记忆、灵活运用不等式知识.

一、培养与加强学生的数学思维能力

在高考试题中，不等式知识通常会与三角、方程、函数等知识结合在一起，并以此来考查学生的思维能力、解题能力.

例如，（2014安徽，文13）设函数f（x）=2|x-1|+x-1，g（x）=16x2-8x+1，记f（x）≤1的解集为M，g（x）≤4的解集为N.

（Ⅰ）求M；

（Ⅱ）当x∈M∪N时，证明x2f（x）+x[f（x）]2≤14.

本题考查不等式选讲、含绝对值不等式的解法、不等式的证明等，解答本题的关键是能利用分类讨论思想，去掉绝对值，转化成为常见不等式求解.本题（Ⅱ）转化成二次函数的图像和性质问题求解，实现了化生为熟的解题策略.

在此题的教学过程中，教师先要引导学生找出试题中的已知信息，并运用已有知识来分析、转化、解决问题.通过科学、合理地分析问题、解答问题，不仅改善了学生的解题能力，在一定程度上也加强了学生的数学思维能力和转化与化归思想.那么，学生再碰到这种问题就会游刃有余了.

二、实现教学生活化

在不等式教学过程中，将不等式知识与三角、方程、函数等知识有机联系起来进行教学，可以提高学生对知识的灵活运用能力，使学生更快、更准确地解答试题，但也大大增加了学生对数学知识的学习难度.面对这样的问题，可以通过将不等式教学与生活中常见的实例结合起来，在生活情境中对不等式知识与其他知识进行结合教学，有利于提高教学效率与教学效果.例如，在讲解关于利用不等式对最值进行求解的知识时，教师就可以结合生活中的常见实例进行教学.

例如，（2015陕西，理10）某企业生产甲、乙两种产品均需用A，B两种原料.已知生产1吨每种产品需原料及每天原料的可用限额如表所示，如果生产1吨甲、乙产品可获利润分别为3万元、4万元，则该企业每天可获得最大利润为（）

A.12万元

B.16万元

C.17万元

D.18万元

甲乙原料限额

A（吨）3212

B（吨）128

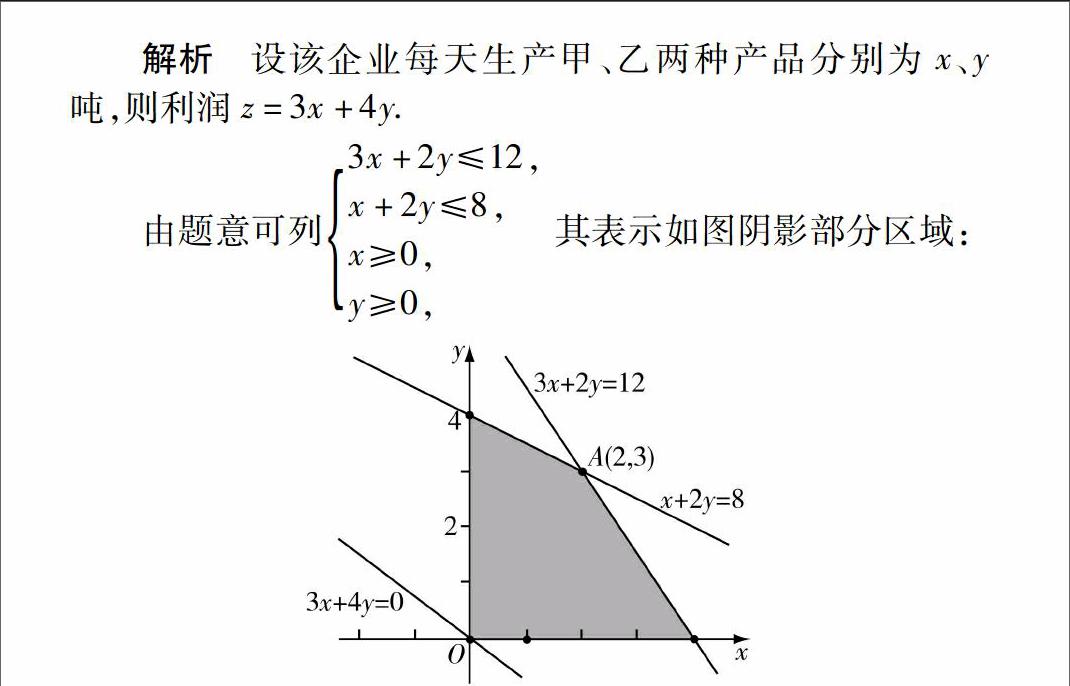
解析设该企业每天生产甲、乙两种产品分别为x、y吨，则利润z=3x+4y.

由题意可列3x+2y≤12，x+2y≤8，x≥0，y≥0， 其表示如图阴影部分区域：

当直线3x+4y-z=0过点A（2，3）时，z取得最大值，所以zmax=3×2+4×3=18，故选D.

引用这一实例，学生理解了利用不等式对最大值进行求解，就是对利润的最大值进行求解，从而使学生更容易理解关于不等式最值的概念，之后教师再引导学生对不等式最值的知识点及习题等进行练习，从而可以使学生更好地掌握、牢固记忆不等式最值的相关知识.

三、综合性提高

在高考试题中，通过不等式的基本知识、基本方法在代数、三角函数、数列、复数、立体几何、解析几何等各部分知识中的应用，深化数学知识间的融会贯通，從而提高分析问题、解决问题的能力.而在应用不等式的基本知识、方法、思想解决问题的过程中，又提高学生数学素质及创新意识.

例如，（2013四川，理21）已知函数f（x）=x2+2x+a，x<0，lnx，x>0， 其中a是实数.设A（x1，f（x1）），B（x2，f（x2））为该函数图像上的两点，且x1

（Ⅰ）指出函数f（x）的单调区间；

（Ⅱ）若函数f（x）的图像在点A，B处的切线互相垂直，且x2<0，求x2-x1的最小值；

（Ⅲ）若函数f（x）的图像在点A，B处的切线重合，求a的取值范围.

解决函数、导数的解答题要充分注意数学思想方法的应用以及不等式的应用.此题中，从第一步到第三步，简单不等式的解法、绝对值不等式的解法、不等式恒成立问题等始终贯穿着整道题.

四、结束语

在不等式的学习和高考试题中，对于不等式的考查主要是基于其作为解题工具，进而培养学生对数学问题和实际问题的解决能力和抽象化的数学思维能力.这就要求教师充分掌握数学教育理论和高考指导思想，将其充分落实到教学过程中，满足学生各方面的需求，培养学生发散思维和探索、创造能力.使学生能够准确掌握、牢固记忆、灵活运用不等式知识，最终可以更好地面对高考，取得理想的成绩.