基于学习共同体的导数的应用教学案例研究

钟时泉

【摘要】本文以“共同体”的提出为出发点，研究在高中课堂上构建学习共同体的教学实施策略，通过以“导数的应用”为例的教学实践的实验，探究如何在高中数学课堂上推广学习共同体理念下的高中数学课堂教学模式.

【关键词】学习共同体；教学设计；课堂教学

一、引言

（一）研究背景

自高中课程教学改革以来，广大教师的教育理念和教学方式均发生了很大的变化.人本主义思想、主体教育观念、建构主义理论不停地为“课堂教学”的机体注入新的活跃细胞，但是课堂教学依然是令人担忧.从全校高中部三个年级段随机抽取了一班学生（共170人）做了问卷调查，问题答卷情况如下：

1.你认为个人学习成功的快乐主要来源于？

70%的自己的感觉，26%的来自老师的肯定，有4%的来自同学的肯定.

2.你不爱学习的原因是：有62%的学生认为学习没有成就感，6%的学生认为学习不会带来直接利益，32%的学生认为学习太苦太累.

3.你认为提高学习成绩的有效方法是：70%上课好好听讲，26%平时多做练习，4%平时多与同学、老师探讨.

4.目前，71%的老师讲课在35分钟以上；23%的25分钟左右，有9%的老师在15分钟左右.

通过以上调查结果可以看出，旧的学习经验在学生意识当中的定式根深蒂固，导致主动学习的意识匮乏，学习动力不足；由于当今社会众多因素的影响，学生自我意识强烈，合作意识严重缺失；教师的教育观念与思想更新不及时，忽略了学生的主体地位，忽视调动全体学生学习的积极性、主动性、参与性；在教学策略上，教师在引导学生自主探究知识的教学过程中调控不力.

（二）课堂“学习共同体”特征

1.和谐互动的课堂

课堂学习共同体是一个有机的、和谐的系统，在这个系统中，学习者和助学者在一个特定的环境中互动，以完成共同认为有价值的活动和任务.

2.具有共同愿景

美国杰出的管理大师彼得·圣吉的《第五项修炼—学习型组织的艺术与实务》版，在该书中他认为“共同愿景最简单的说法是我们想要创造什么，正如个人愿景是人们心中或脑海中所持有的意象或景象，共同愿景也是组织中人们所共同持有的意象或景象，它创造出一体的感觉，并遍布到组织全面的活动，而使不同的活动融合起来”.课堂学习共同体成员通过沟通、协商确定共同愿景，每个成员在实现个人愿景的同时，团结协作，为实现共同愿景而共同努力.

3.具有共同的课堂规范

课堂教学是错综复杂的，要把课堂建设成学习共同体，必须有成员共同协商制订并认可，且自觉遵守课堂规范，这样成员才能更好地处理好个人利益与共同利益之间的矛盾，确保顺利地完成共同的学习任务.

4.课堂文化氛围宽松积极

课堂要创建一个宽松积极的课堂文化氛围，为共同体成员的学习创造有利条件，使每个成员积极上进，乐于共同开展课堂活动，从而发挥自己的最大潜能，最终胜利完成学习共同体的学习任务.

三、实施策略的总体框架

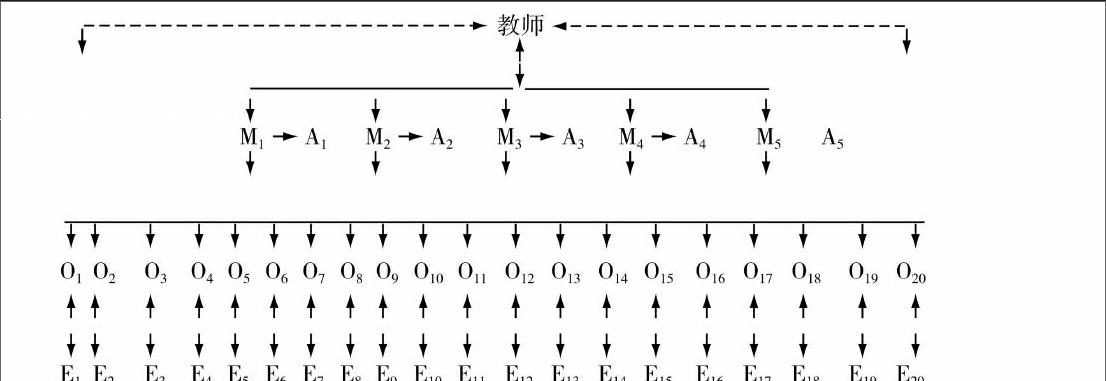
学习共同体的载体主要依赖小组的合作学习，学习小组不再是传统教学的小组，现在的学习小组不仅具备共同学习职能，还具备管理职能.各班级学习小组组成拟定遵循“自主、轮选”“班干部不同组”“男女生搭配”“组间均质，组内异质”“每组不超6人，以6或4人为宜”五项原则.

如图示：说明：M（课代表），A（重点目标生），O（临界生），E（发展生）

构建“学习共同体”课堂需突破的重点：

1.彻底转变教师传统的教学观念和教学模式，改变学生的学习方式，让学生真正成为学习的主人.

2.教学评价的转变应从如下的转变：（1）评价内容需考虑到课堂教学的系统要素、过程要素、课堂教学结果、学生的参与度等各个方面；（2）评价主体变为课堂中的师生评价；（3）评价方法多样化，把日常观察、成长记录袋、真实性评价等方法相结合；（4）由总结性评价向过程性评价转变.

3.师生之间的互动包括两类：一是教师的示范活动；另外是成员之间的同伴式的互助，在互动中师生共享经验，达成共识，实现着跟实际情况相符合的社会化.

四、以“导数的应用”为例的学习共同体课堂教学设计

（一）教材分析

“导数及其应用”这一章内容在《普通高中新课程标准实验教科书数学选修》教材中，它虽是在选修教材之中，但是文理科必选内容.该内容是学生在文理分科后学习，无论是文科学生还是理科学生都对导数的学习倍感困惑.试卷中的问题重点考查的是数学思维，导数的思想方法的渗透是重中之重.问题的解决更依靠扎实的数学基本功、优秀的思维品质和分析、解决问题的能力.

（二）学情分析

学生在高一学完了函数模型，对三种函数增长模型有了初步的了解，而对于把数学问题从特殊过渡到一般、解题中的换元思想使用比较吃力.

（三）教学内容

1.学生用几何画板作图，通过图像直观感知函数y=xn（n>0）与y=logax（a>1）图像关系；

2.借用導数设置相应的问题，师生共同讨论一起探究函数y=xn（n>0）与y=logax（a>1）图像关系；

（四）教学重点与难点

1.教学重点：理解并掌握由特殊函数的研究到对一般函数的研究过程.

2.教学难点：体会由定性描述到定量研究函数y=xn（n>0）与y=logax（a>1）图像关系的过程.

（五）教学方法与手段

教法：问题引导法、问题探究法

教学手段：几何画板

（六）教学过程

教学流程设计如下：

问题引入问题探究问题小结

教学过程：

问题引入

对数函数y=logax（a>1）和幂函数y=xn（n>0），总会存在一个x0，当x>x0时，就有logax

【预设答案】只能通过图像进行“直观感知”，但会给我们带来困惑：（1）我们看到的这部分图像是否可靠？（2）看不到的部分图像是否真的如我们想象中的样子？所以引入“定量分析”是必要的，这也是用数学研究问题的方式.

[设计意图]学生分小组讨论后，通过图像直观感知函数y=logax（a>1）和幂函数y=xn（n>0）的图像关系.

问题探究：

问题1：证明：存在x0，当x>x0时，有x>lnx.（教材习题）

[设计意图]教师通过最特殊的幂函数和对数函数入手进行研究.学生通过教师设置的问题，进行思考，并回答问题.

问题2：是否存在x2≥0，使得当x∈（x2，+∞），x>lnx？（分小组进行讨论.）

【预设答案】

令t=x，t>0.所以x=t2.

证明：存在t0，当t>t0时，有t>2lnt.

记f（t）=t-2lnt（t>0），f′（t）=t-2t，令f′（t）=0t=2，

当t∈（0，2）时，f′（t）<0，f（t）单调递减；当t∈（2，+∞）时，f′（t）>0，f（t）单调递增.

所以，f（t）min=f（2）=2-ln4>0，故对任意x∈（0，+∞），有x>lnx.

【设计意图】教师通过设置对不同的幂函数与自然对数函数图像关系的研究，再次强化学生利用导数对函数图像关系进行定量研究.学生通过动手计算，利用导数工具进行证明.

问题3：证明：当n>0，存在x0，当x>x0时，有xn>lnx.

【预设答案】

令t=xn，t>0，

即证明：当n>0时，存在t0，当t>t0时，t>1nlnt，

记f（t）=t-1nlnt（t>0），f′（t）=nt-1nt（t>0），

令f′（t）=0t=1n，

当t∈0，1n时，f′（t）<0，f（t）单调递减；

当t∈1n，+∞时，f′（t）>0，f（t）單调递增.

所以，f（t）min=f1n=1n1-ln1n.

[设计意图]教师通过到一般的幂函数与自然对数函数图像关系的研究，在处理问题的过程中，合理的利用已得结论解决问题的意识，学生完成后续的解题过程.

问题4：证明：当n>0，存在x0，当x>x0时，就有logax

【预设答案】

换底公式：logax=lnxlna，

原问题转化为证明：当n>0，存在x0，当x>x0时，就有lnx

令t=xn，t>0，则x=t1n，

原问题转化为证明：

当n>0，存在t0，当t>t0时，就有lnt

[设计意图]通过前面对特殊问题的解决，最后得到对一般性的问题的解决：幂函数与自然对数函数图像关系的研究，要增强利用已得结论解决问题的意识，学生完成后续的解题过程.

问题5：讨论函数f（x）=lnxx的性质.

问题6：（2014湖北卷）π为圆周率，e=2.71 828…为自然对数的底数，求e3，3e，eπ，πe，3π，π3这六个数的最大数与最小数.

问题7：证明：当n>0，存在x0，当x>x0时，就有xn

五、教学反思

在课堂中学习共同体的活动需要助学者不断地变换角色，因此，要求教师具备更强的组织能力、交流能力和更为完善的学科知识体系.“学习共同体”在探究、交流的过程中完成一定的教学任务需要较多的时间，而课堂教学中哪一类型的教学任务更适合于这种学习组织形式有待于进一步研究.

六、结语

在高中课程改革的背景下，要更加关注课堂教学，服务课堂教学.每位教育工作者在课堂改革的道路上为提高课堂教学质量进行探索与实践.本文就构建了基于学习共同体下的高中数学课堂模式，并提出实施策略，包括实施的总体框架、基本内容、需突破的重点以及需解决的关键问题等，期待为课堂教学优化提供一种可借鉴的模式.