欣赏绽放的函数之花,体验动态的数学之美
2017-04-18董正武
董正武
【摘要】在“幂函数”的教学中,当学生自主探究完y=x-1,y=x0,y=x,y=x2等幂函数的图像与性质时,有一个明显的感受是:幂函数的图像与指数函数、对数函数的图像相比情形较为复杂.本文借助幾何画板,动态地探究幂函数(其中α≠0,1)在第一象限的图像与性质,以飨读者.
【关键词】幂函数;几何画板;动态;图像与性质
一、利用几何画板画幂函数的图像
(1)在x轴的负半轴构造一点A,过A作x轴的垂线j.
(2)在j上构造一点B,选中点A,B,构造线段AB,隐藏垂线j.
(3)度量点B的纵坐标,将标签设置为α.
(4)单击【绘图】中的【绘制新函数】,键入y=xα.
二、幂函数之花即将绽放
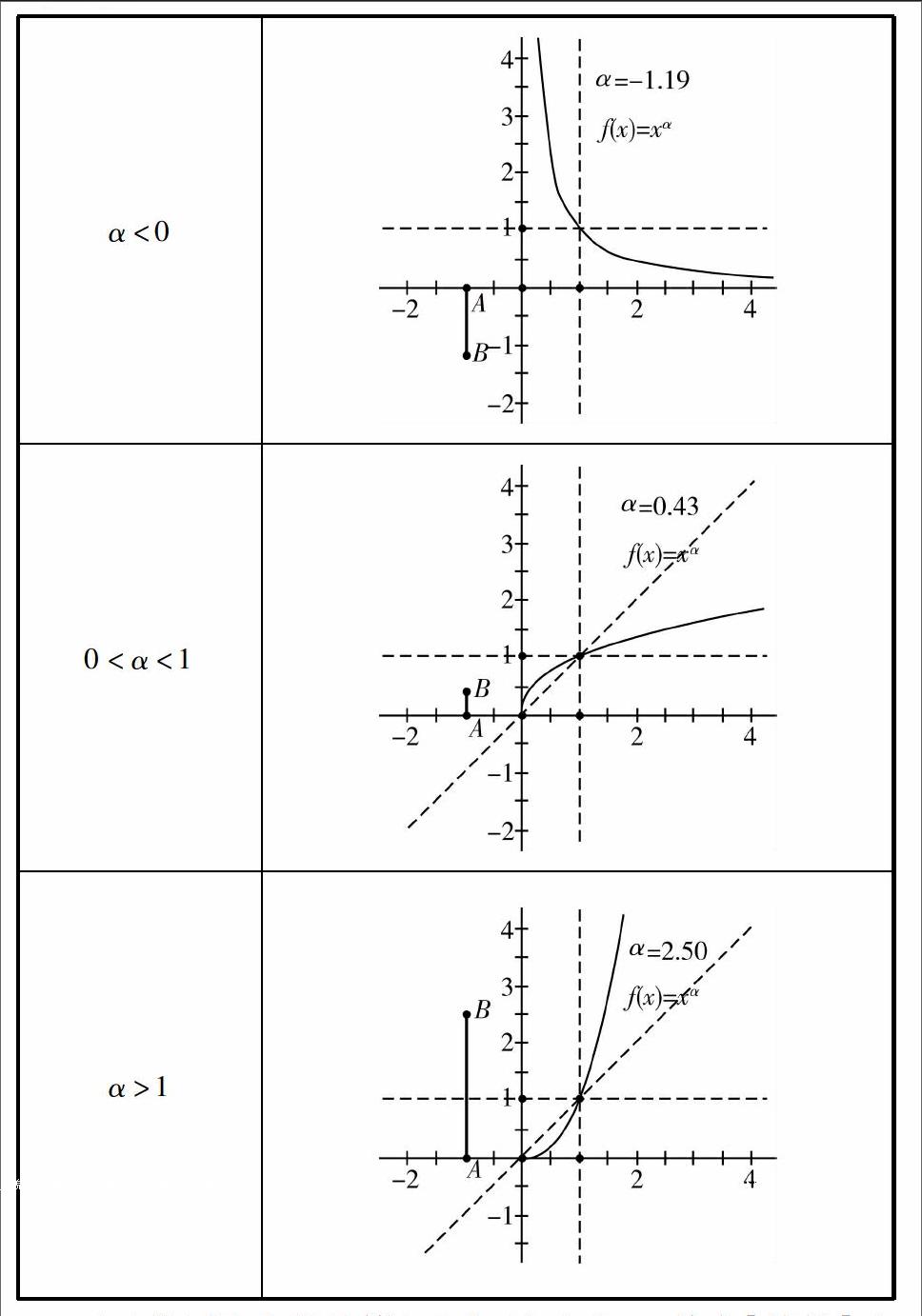
(5)上下拖动点B,改变α的值,观察y=xα的图像变化情况如下.
α<0
0<α<1
α>1
(6)接画法步骤的第(5)步,选中点B,单击【编辑】中的【操作类按钮】,选择动画.
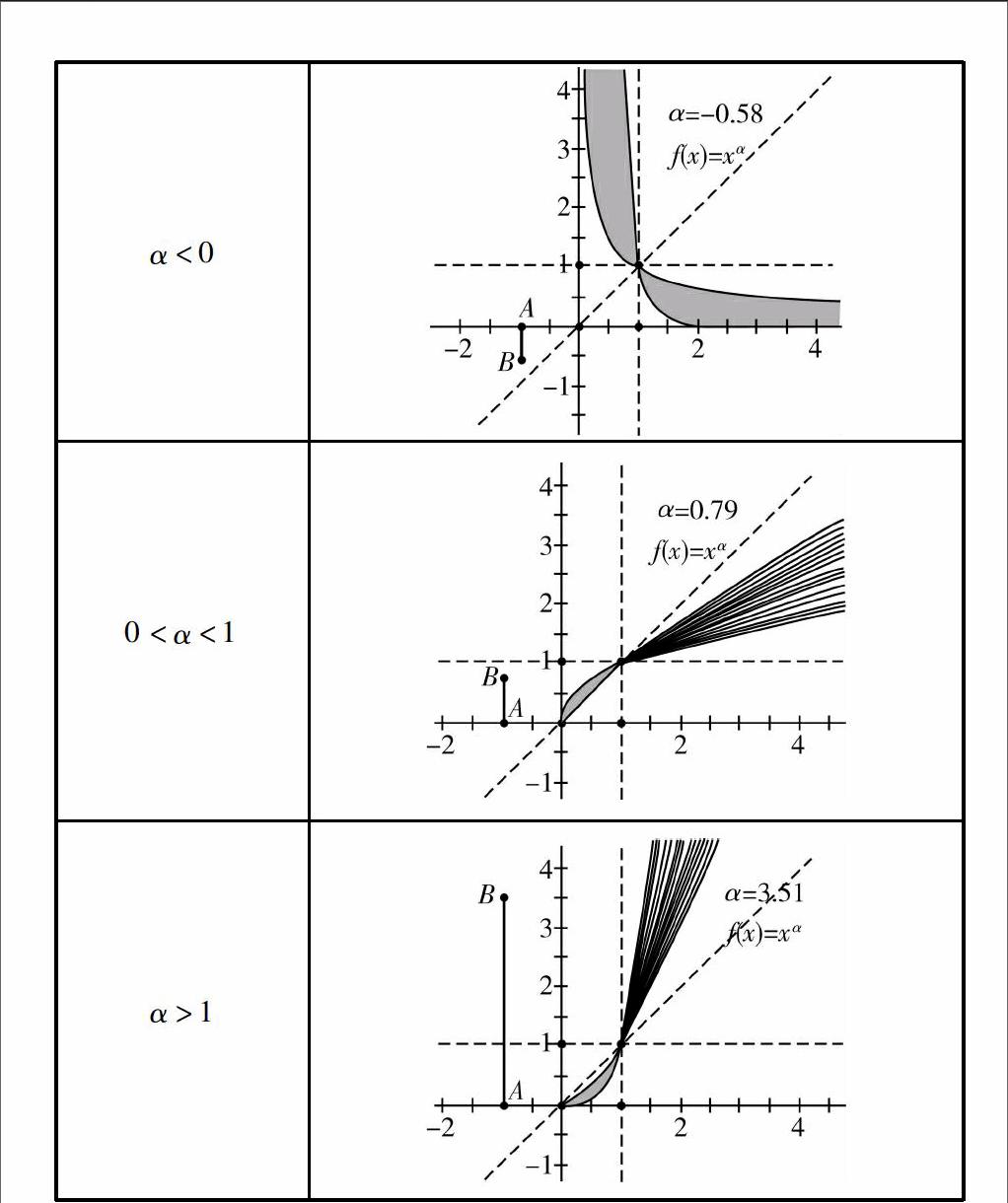
(7)选中点B及图像,单击【构造】中的【轨迹】,观察幂函数图像的动态变化.
α<0
0<α<1
α>1
三、幂函数的性质
(一)相同点:过定点(1,1).
(二)不同点:
(1)单调性:当α<0时,在区间(0,+∞)上单调递减,当α>0时,在区间(0,+∞)上单调递增.
(2)函数值变化:当α<0时,若x∈(0,1),则y∈(1,+∞);若x∈(1,+∞),则y∈(0,1).当α>0时,若x∈(0,1),则y∈(0,1);若x∈(1,+∞),则y∈(1,+∞).
(3)图像形态特征:当0<α<1时,若x∈(0,1),则图像在y=x上方(称为上凸);若x∈(1,+∞),则图像在y=x下方.图像先陡峭、后平缓,增长速率是先快后慢.当α>1时,若x∈(0,1),则图像在y=x下方(称为下凸);若x∈(1,+∞),则图像在y=x上方.图像先平缓、后陡峭,增长速率是先慢后快.
(三)图像随α变化情况:当α<0时,随着α逐渐增大,在(0,1)上的图像越来越靠近y轴,在(1,+∞)上的图像越来越远离x轴;如果α→0,那么图像趋近于y=1.
当0<α<1时,随着α逐渐增大,在(0,1)上的图像突出y=x的部分越来越少;如果α→1,那么图像趋近于y=x.
当α>1时,随着α逐渐增大,在(0,1)上的图像突出y=x的部分越来越多.
四、授课感受
波利亚说道:“观察可能导致发现,观察将揭示某种规则模式和定律.”当我们观察幂函数图像的变化时,我们就会体验到无穷的动态之美,体会“数与形”的高度统一,让我们用“运动”的观点研究数学吧!
【参考文献】
[1]陶维林.几何画板课件制作教程[M].北京:人民教育出版社,2005.
