用分子动力学方法预测硅纳米薄膜的热导率
2017-04-17白素媛李晶晶王立凡支明蕾
白素媛, 李晶晶, 王立凡, 支明蕾, 王 斌
(辽宁师范大学 物理与电子技术学院,辽宁 大连 116029)
用分子动力学方法预测硅纳米薄膜的热导率
白素媛, 李晶晶, 王立凡, 支明蕾, 王 斌
(辽宁师范大学 物理与电子技术学院,辽宁 大连 116029)
采用非平衡分子动力学方法,基于优化的集成势函数COMPASS力场,预测了室温下(300 K)硅纳米薄膜的热导率.模拟结果表明:厚度约4~10 nm的硅薄膜的热导率在3.06~7.28 W/(m·K)范围,并且随着膜厚的增加而增大,表现出明显的尺度效应.在所计算的薄膜厚度范围内,硅纳米薄膜的热导率与薄膜厚度呈现近似线性变化的关系.应用气动理论对产生的尺度效应进行了初步的理论分析,当薄膜厚度在几纳米到十几纳米时,有效声子平均自由程与膜厚有关,不再等于体材料的平均自由程.同时也将本文的预测结果与其他研究者采用Stillinger-Weber势所进行的模拟结果进行了比较.为分子动力学方法在低维材料热物性方面的研究提供了有益的参考.
分子动力学方法;热导率;硅纳米薄膜;尺寸效应
薄膜作为二维低维材料广泛应用于微电子器件及微机电系统,伴随着器件特征尺寸的不断减小,薄膜厚度已经进入到纳米量级.薄膜热物性通常不同于体材料.热物性,特别是热导率直接影响器件和系统的稳定性和可靠性.由于现阶段商用的热物性测试仪器对于微纳米薄膜热导率测试还存在非常大的困难,采用分子动力学方法对纳米尺度薄膜的热导率进行预测成为行之有效的方法.该方法按照分子系统的时间演化来进行,并由此产生被研究体系内部相互作用分子的详细运动轨迹,进而可以求出平衡或偏离平衡情况下分子体系的动力学性质.在分子动力学方法中,研究的分子体系是确定的,分子体系又严格遵守物理定律.由于该方法不需要对几何对称、输运性行为、热力学行为等作先验假设,热力学及输运性质直接就是计算结果,因此亦被看作“计算机实验”[1-2].
硅是微电子器件和微机电系统中最重要的薄膜材料之一,因此用分子动力学方法对硅纳米薄膜热导率的研究成为当前一个研究热点[3-6].但由于人们选用的方法存在不同、采用的力场也不相同,研究系统的尺寸以及温度范围不同,这些都导致当前得到的硅纳米薄膜热导率的相关结果存在差异性及数据的零散性,还需要进一步验证和明确.
针对厚度范围约在4~10 nm的硅薄膜在室温下(300 K)的热导率进行了分子动力学模拟计算,采用的是非平衡动力学方法,在作用势的选择上,采用了优化的集成的势函数COMPASS力场[7].
1 非平衡分子动力学方法
依据模拟过程中体系所处的热力学状态,分子动力学方法分为两大类别:第一种是平衡分子动力学方法;第二种是非平衡分子动力学方法.平衡分子动力学方法主要根据线性响应理论中Green-Kubo公式所建立的输运系数与平衡时间相关联来获得模拟体系的热导率;非平衡分子动力学方法主要根据体系内的温度分布和热流密度情况由Fourier定律获得热导率.由于本文选择了第二种方法,所以下面将重点介绍它.
在非平衡分子动力学方法中,需要建立起一个非平衡输运模型.这个非平衡输运模型通过对系统施加扰动来形成,比较常用的扰动方式是加入温度梯度或者加入热流.图1即为本文模拟体系所建立起来的模型.模拟体系用三维空间坐标X、Y、Z表示,3个坐标方向上都取周期性边界条件,在待考查的薄膜厚度Z方向上建立起稳态的非平衡热输运过程.实现的具体方法是:沿Z方向将体系均匀地分成多个层,使每层中所包含的原子数目相等或接近相等,将处于Z坐标1/4和3/4处的层分别作高温控制层和低温控制层(控温层可以是1个或多个).当然,由于采用了周期性边界条件,控温层不是必须选在前面所述的位置上的,只需要选择满足2个控温层的中心处相距等于模拟体系厚度的一半就可以.本文所提到的薄膜厚度即为模拟体系厚度的一半.

图1 非平衡输运模型
2 COMPASS力场
正确选择被模拟材料系统的相互作用势,是使用分子动力学方法进行准确模拟的前提.相互作用势一般由势函数来描述,它实际上描述的是电子云重叠的量子力学作用结果.由于材料的复杂性,大多数原子的排列的精确势函数目前仍不明确,因此经验或半经验的势函数常被采用,比如应用最为广泛的对势L-J势[8]、包括两体项及三体项的Stillinger-Weber势[9]和Tersoff势[10]等.另外还有集成的势函数文件,被叫作力场,比如UNIVERSAL[11]、DERIDING[12]、COMPASS力场[7]等.由于COMPASS是新近发展起来的适合凝聚态应用的一个全新力场,具有更多的优点和先进性,因此本文选择了该力场.
COMPASS力场是采用从头计算方法并结合实验数据经验参数化技巧而研发出来的.分子内的键参数主要由从头计算方法得到;范德华非键合参数通过分子动力学模拟结果和实验数据相结合方法而获得,也就是:除了像一般的分子力场通常所要考虑的两个实验数据(X光和振动光谱)作为参照之外,COMPASS力场还采用对液态分子动力学模拟得到的结合能、液态密度等同时作为参数化的实验标准,从而得到了更加优化的力场性能.COMPASS力场的势函数形式如下:
函数展开式由13个统计求和项构成,其内容可划分为两种项目:键合项和非键合项.键合项由展开式的前11个统计求和项构成,包括对角和非对角的交叉耦合项,主要由键长(b)、键角(θ)、二面角(φ)、面外角(χ)及含有上述参数两个以上的耦合项构成.非键合项对应展开式中最后两个统计求和项,包括范德华能和库仑能.非键合项中,q为电荷量,rij为i原子与j原子间的距离.函数展开式中其他参数的意义为:k、H、V、A、B为力常数,ε为能量参数.
3 结果与讨论
采用非平衡分子动力学方法模拟计算了厚度分别为4.344、5.430、6.516、7.602、8.688、9.744 nm(分别对应在Z方向上取16、20、24、28、32、36个基本单元的超级晶胞)的硅薄膜的热导率,系统温度为300 K,时间步1.5 fs,计算步数300万步.
以厚度为8.688 nm的硅薄膜为例,经300万步计算后得到各层的温度分布曲线如图2所示.由图2可以看到,各层的温度分布在高低控温层之间所形成的曲线是比较光滑的.浅色圆点分布区域即为控温区,控温区内存在温差,但这是合理的,因为有热流从该区域通过,因此必然也有温差.
在非平衡动力学方法中,稳态的非平衡过程的建立十分关键,它也可以通过检查得到的薄膜热导率随计算步数的变化而趋于不变得以确认.仍以8.688 nm的硅薄膜为例,图3所示的是它的热导率随计算总步数的变化情况.可以看到,80万步(横坐标刻度乘以200×103等于总计算步数)之前,热导率波动较大,而到了约160万步之后,热导率变化已经非常微小,因此300万步的计算时间是满足建立稳态非平衡过程的.
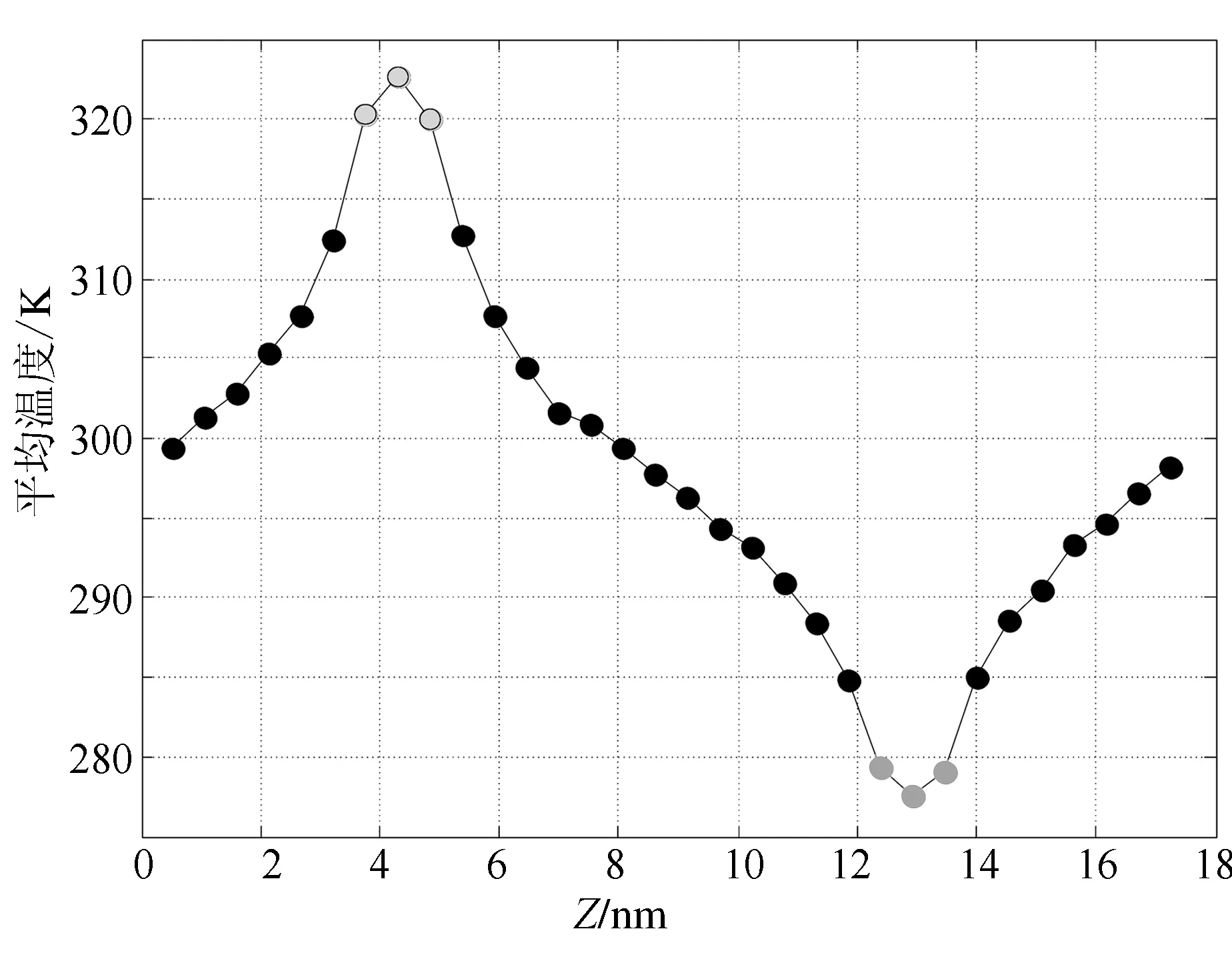
图2 厚度为8.688 nm的硅薄膜中各层的温度分布情况
温度300 K下硅纳米薄膜的热导率的模拟结果列在表1中.厚度范围在4.344~9.744 nm 的硅薄膜的热导率在3.06~7.28 W/(m·K)范围.热导率随膜厚的变化关系如图4所示.由图4可以看到,在所计算的厚度范围内,硅薄膜的热导率随着薄膜厚度的增加而增加,接近于线性变化,表现出明显的尺度效应,且远低于体材料值.

表1 硅纳米薄膜的热导率的计算结果

图4 热导率随膜厚的变化
由气体动力学理论导出的介质导热系数表达式为[13]
(2)
其中,c是体积比热容,v是声子的平均速度,leff是材料的有效声子平均自由程.当薄膜的厚度d远大于体材料的声子平均自由程l∞时,leff=l∞;当薄膜厚度d只有几个纳米到十几个纳米时,leff远小于声子平均自由程l∞,此时,有效声子平均自由程leff由膜厚d所决定,因此,热导率与膜厚呈现出近似的线性关系.在声子气动理论中,影响晶格热导率的决定因素是声子的有效平均自由程leff,而影响有效声子平均自由程的因素很多,如边界对声子的散射、缺陷和杂质对声子的散射、声子与声子间的散射等.
文献[6]中利用Stillinger-Weber势计算了300K下厚度在2.715~54.30nm的硅薄膜的热导率,他们在低于20nm的厚度范围内,观察到了热导率与膜厚呈近似线性关系,20nm以上厚度的薄膜的热导率仍随厚度增加而增加,但增加趋势变缓.在与本文研究相近的厚度范围内,他们得到3~10nm的硅薄膜的热导率约在3.5~12W/(m·K),本文采用COMPASS力场得到的结果与之相接近,并且同样得到了热导率与膜厚之间近似线性变化的关系,可见本文的预测是合理的和可信的,至于还存在差异性,是由于选择不同力场的原因.后继工作将对更大厚度范围内硅薄膜的热导率开展进一步的研究.
4 结 论
采用COMPASS力场,运用非平衡分子动力学方法计算了室温下硅纳米薄膜的热导率.稳态的非平衡过程的建立十分关键,通过选择合适的时间步和计算总步数,通过观察模拟系统各层温度分布情况以及热导率随计算时间趋于稳定来确保非平衡过程进入稳态.模拟结果表明,厚度为4.344~9.774nm范围的硅薄膜的热导率在3.06~7.28W/(m·K)范围,并且随着膜厚的增加而增大,呈近似线性变化的关系.对于观察到的尺度效应,用气动理论进行了初步的理论分析.研究结果与采用Stillinger-Webber势研究硅薄膜热导率的文献中的结果基本一致,为分子动力学方法在低维材料热物性研究的应用提供了有益的参考.
[1] KOTAKE S,WAKURI S. Molecular dynamics study of heat conduction in solid materials[J].Fluids and Thermal Engineering,1994,37(1):103-108.
[2] 杨小震.分子模拟与高分子材料[M].北京:科学出版社,2002:2-5.
[3] 肖鹏,冯晓利,李志信.单晶硅薄膜法向热导率分子动力学研究[J].工程热物理学报,2002,23(6):195-199.
[4] 吴国强,孔宪仁,孙兆伟,等. 单晶硅薄膜法向热导率的分子动力学模拟[J].哈尔滨工业大学学报,2007,39(9):1366-1369.
[5] 华钰超,董源,曹炳阳. 硅纳米薄膜中声子弹道扩散导热的蒙特卡罗模拟[J].物理学报,2013(24):178-186.
[6] WANG Z H,LI Z X. Research on the out-of-plane thermal conductivity of nanometer silicon film[J].Thin Solid Films,2006,515:2203-2206.
[7] SUN H. COMPASS:An ab initio force-field optimized for condensed-phase applications-overview with details on alkane and benzene compounds[J].J Phys Chem B,1998,102(38):7338-7364.
[8] LENNARD-JONES J E. On the determination of molecular fields[J].Proc R Soc A,1924,106(738):463-477.
[9] STILLINGER F H,WEBER T A. Computer simulation of local order in condensed phases of silicon[J].Physical Review B,1985,31(8):5262-5271.
[10] TERSOFF J. Empirical interatomic potential for silicon with improved elastic properties[J].Physical Review B,1988,38(14):9902-9905.
[11] DAUBER-OSGUTHORPE P,ROBERTERS V A,OSGUTHORPE D J, et al. Structure and energetics of ligand binding to proteins:Escherichia coli dihydrofolate reductase-trimethoprim,a drug-receptor system[J].Proteins:Structure,Function,and Genetics,1988,4(1):31-47.
[12] MAYO S L,OLAFSON B D,GODDARD W A. DREIDING:A generic force field for molecular simulations[J].J Phys Chem,1990,94(26):8897-8909.
[13] TAMMA K K,ZHOU X. Macroscale and microscale thermal transport and thermo-mechanical interactions-some noteworthy perspectives[J].Journal of Thermal Stress,1998,21(3/4):405-449.
Prediction of the thermal conductivity of nanometer silicon films by molecular dynamics simulations
BAISuyuan,LIJingjing,WANGLifan,ZHIMinglei,WANGBin
(School of Physics and Electronic Technology, Liaoning Normal University, Dalian 116029, China)
Thermal conductivities of a serial of nanometer silicon films with thickness of 4~10 nm are calculated by no-equilibrium molecular dynamics method and an ab-initio force field, COMPASS. At room temperature (300 K), the thermal conductivities are 3.06~7.28 W/(m·K). The calculated results show that the thermal conductivity of nanometer silicon film decreases with the decrement of film thickness and is significantly lower than the bulk value. A notable size effect is observed due to the approximate linear relationship between the thermal conductivity and the film thickness. Phonon aerodynamic theory is employed to explain the size effect. The predicted results agree well with the results of other researcher’s obtained with Stillinger-Weber potential model. This work will be helpful in applying molecular dynamic simulations to study the thermal properties of low dimension materials.
molecular dynamics simulation;thermal conductivity;nanometer silicon film;size effect
2016-11-20 基金项目:辽宁省自然科学基金资助项目(2015020079) 作者简介:白素媛(1971-),女,辽宁海城人,辽宁师范大学副教授,博士.Email:dl_bsy@163.com
1000-1735(2017)01-0030-05
10.11679/lsxblk2017010030
O484;TK124
A
