具有随机保费离散半马尔可夫风险模型的生存概率

包振华, 王 翠

(辽宁师范大学 数学学院, 辽宁 大连 116029)

具有随机保费离散半马尔可夫风险模型的生存概率

包振华, 王 翠

(辽宁师范大学 数学学院, 辽宁 大连 116029)

半马尔可夫风险模型通过构造一个外在的马尔可夫环境来刻画保险公司所处环境的变化,可以用来处理保险公司在实际运营过程中出现的各种相依关系.考虑到保险实践中保费收入具有不确定性，构建一类具有随机保费收入的离散半马尔可夫风险模型,其中保费收入由一个独立的二项过程来刻画.利用概率生成函数的技巧,给出生存概率所满足的递归计算公式.建立了生存概率在零初值时所满足的2个线性方程，通过求解线性方程组可以给出零初值时生存概率的解析表达式，进而利用递归公式得到任意初值的生存概率.作为应用,最后对理论结果做了数值分析.

半马尔可夫风险模型;随机保费;生存概率

在风险理论中,马尔可夫调节的风险模型通过构造一个马尔可夫外在环境来处理保险公司实际运营中出现的各种相关关系,因而受到了保险精算理论和实践者的广泛关注.离散半马尔可夫风险模型假设索赔额受一个环境马尔可夫链控制,此类模型最早由Reinhard和Snoussi[1-2]提出,他们得到了破产前盈余分布的递归计算公式.最近,Chen等[3-4]放松了文献[1-2]中关于模型的一些设置条件,分别得到了期望贴现红利以及生存概率满足的递归公式.然而,上述文献中都假设单位时间的保费收入为常数,这种限制一般不符合保险实践.Temnov[5]最早在模型中使用一个复合泊松过程来描述保费收入,而用另一个独立的复合泊松过程刻画索赔额,得到了破产概率所满足的卷积公式.此后,有众多保险精算文献研究具有不同形式的随机保费收入模型,参见文献[6-7]及所引文献.本文考虑具有随机保费收入的半马尔可夫风险模型,得到了生存概率满足的递归计算公式,并对理论结果做数值分析.

1 模型结构

(1)

其中，u∈为保险公司的初始盈余,非负整值随机变量序列{Yi,i=1,2,…}表示索赔过程,并且Yt的分布是受环境马尔可夫链影响,即Yt和Jt的条件联合分布为

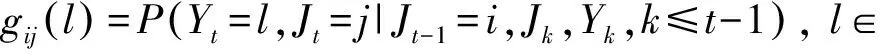
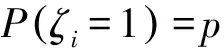
2 生存概率满足的递归公式

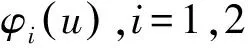
(2)

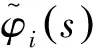
(3)

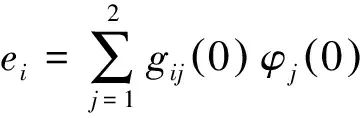
(4)

解线性方程组(4)得

(5)

为了简化符号,定义

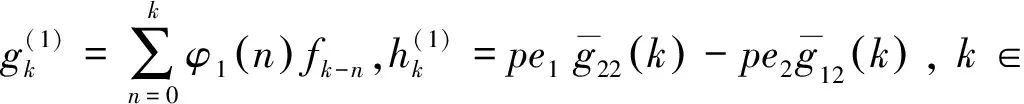
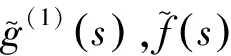
(6)

由式(6)得

(7)

(8)

定理1 对于i=1,2以及k∈+,生存概率满足递归计算公式:

(9)

证 由式(7)和式(8),只需说明当f0=0且f1=0时不等式π1μ1+π2μ2≥1成立.注意到

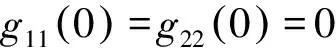
(10)

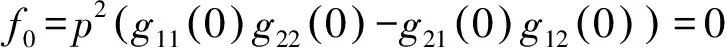
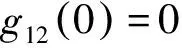
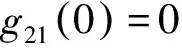
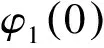
等价地

(11)

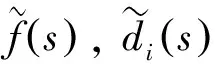
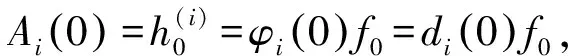
(12)

在式(12)两边关于s求导得

(13)

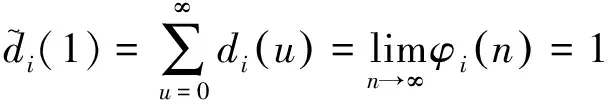
(14)

其中，

经计算得

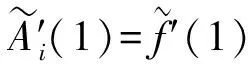
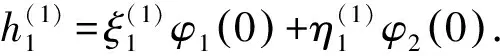
(15)

其中，

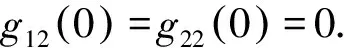
(16)

现在考虑f0>0.令

(17)

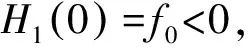
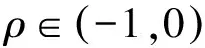
3 数值分析

数值分析只考虑f0=0的情形,其他情形类似.索赔分布(表1)引自文献[4].注意到当p=1时，模型(1)即退化为文献[4]中的风险模型.

表1 索赔的分布

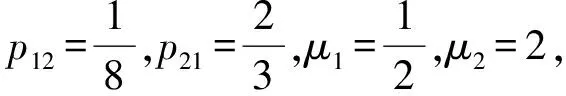
表和的数值结果

[1] REINHARD J M，SNOUSSI M.On the distribution of the surplus prior to ruin in a discrete semi-Markov risk model[J].ASTIN Bull，2001，31(2):255-276.

[2] REINHARD J M，SNOUSSI M.The severity of ruin in a discrete semi-Markov risk model[J].Stochastic Models，2002，18(1):85-107.

[3] CHEN M，GUO J，WU X.Expected discounted dividends in a discrete semi-Markov risk model[J].Journal of Computational and Applied Mathematics，2014，266(2):1-17.

[4] CHEN M，YUEN K C，GUO J.Survival probabilities in a discrete semi-Markov risk model[J]. Applied Mathematics and Computation，2014，232(2):205-215.

[5] TEMNOV G.Risk process with random income[J].Journal of Mathematical Sciences，2004，123(1):3780-3794.

[6] BAO Z H，LIU H.The compound binomial risk model with delayed claims and random income[J].Mathematical and Computer Modeling，2012,55(3/4):1315-1323.

[7] GAO J W，WU L Y.On the Gerber-Shiu discounted penalty function in a risk model with two types of delayed-claims and random income[J].Journal of Computational and Applied Mathematics，2014,269:42-52.

Survival probabilities with random premiums in a discrete semi-Markov risk model

BAOZhenhua，WANGCui

(School of Mathematics, Liaoning Normal University, Dalian 116029, China)

The semi-Markov risk model describes the changes for the insurance company by constructing an external Markov environment, which can be used to deal with the dependencies arisen in the operation of insurance company. Noting that the premiums received by the insurer are uncertain, we propose a class of discrete semi-Markov risk model with random premiums, in which the premiums are modeled by an independent binomial process. By using the technique of probability generating function, the recursive formulae for survival probabilities are obtained. We set up two linear equations satisfied by the survival probabilities with zero initial and the corresponding analytic expressions can be derived by solving the system of linear equations, then we can get the survival probabilities with arbitrary initials. As an application, the theoretical results are analyzed by a numerical example.

semi-Markov risk model;random premium;survival probability

2016-10-20 基金项目：教育部人文社会科学青年基金资助项目(15YJC910001)；辽宁省高等学校优秀人才支持计划项目(LR2014031)

包振华(1976-),男,辽宁大连人,辽宁师范大学教授,博士.

1000-1735(2017)01-0001-05

10.11679/lsxblk2017010001

O211.67

A