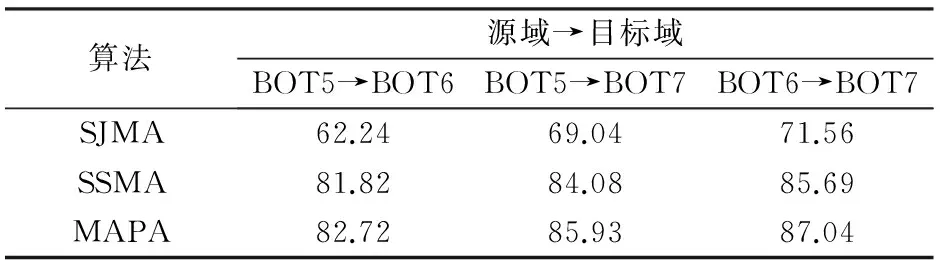
基于流形对齐的高光谱遥感图像降维和分类算法
2017-04-17鲁锦涛马丽
鲁锦涛, 马丽
(中国地质大学(武汉)机械与电子信息学院,武汉 430074)
基于流形对齐的高光谱遥感图像降维和分类算法
鲁锦涛, 马丽
(中国地质大学(武汉)机械与电子信息学院,武汉 430074)
多时相的高光谱遥感图像数据处理中会出现地物光谱特征漂移的现象。为了提高源域数据已有知识对目标域数据分类的精度,采用了基于流形对齐的分类算法。先用一个标准的线性或非线性的降维方法将2个高光谱遥感数据集映射到低维(流形)空间中,再用Procrustes分析方法将其低维嵌入之间的平移、旋转和缩放因子剔除,得到数据集间的最优对齐,最后用最近邻算法进行分类。对多个不同时相高光谱遥感图像进行实验,并对比了已有的流形对齐算法,结果表明本算法具体较好的迁移能力和分类效果。
Procrustes; 流形对齐; 多时相; 高光谱遥感图像; 降维; 分类
0 引言
目前,高光谱遥感已经成为遥感领域的重要分支,其中高光谱遥感影像分类技术更是高光谱遥感处理领域的研究热点。但是高光谱影像分类中存在着这样的难题: 一方面,样本标记的获取需要专家实地考察和标注,这些工作所花费的人力、物力和时间成本往往是非常昂贵的; 另一方面,对于多时相的遥感数据,如果已经标注了部分区域或者某个时间获取的遥感影像,那么对于其他时相的影像,不确定能否在新影像标签数据不足或者没有标签的情况下,利用已有的知识对其进行分类。然而,对于高光谱影像分类,把一个区域或者时间获取的地物特征和标签信息直接应用到同一个场景的另一个区域或者时间获取的影像中可能会出现一些问题,因为对于同一种地物,在不同地理位置或者不同时间,其光谱可能会有比较大的变化,引起这种变化的可能因素包括植被密度和组成、土壤水分、地形和光照条件等等。这种变化将会造成源域高光谱图像中的标签数据的可用性受限。在这种情况下,传统的分类算法无法取得好的分类效果。
近年来,一种被称为流形对齐的迁移学习方法被证明能有效地解决这个问题[1]。流形对齐的主要思想是把不同域特征映射到一个新的共享特征空间,在这个特征空间中,2个域的对应样本数据的特征一致,并且每个域各自的局部或全局几何结构得以保持。实现这种目标的流形对齐算法能够使得源域和目标域数据在新的特征空间中具有相同或相似的分布。
领域适应性研究中,在非遥感领域,如自然语言处理、人脸识别和情感分析等,涌现了很多与流形对齐思想相近的方法。Pan等[2]利用最小化源领域数据与目标领域数据在特征空间上的最大均值偏差求解降维后的特征空间。在这个不同的领域具有相同或者非常接近的数据分布的新特征空间,可直接利用监督学习算法训练模型对目标领域数据进行预测。而Blitzer等[3]通过一种结构对应学习算法把各领域特有的特征映射成所有领域共享的特征,然后在这个特征下进行训练学习。Gu等[4]则探讨了多个聚类任务的学习,提出了一种寻找各个领域的数据共享聚类中心的共享特征子空间的框架。Kan等[5]提出了一种新的目标化源领域数据的领域适应性方法并将其应用于人脸识别。该方法首先将目标领域数据和源领域数据映射到一个共享的子空间,但在该子空间中,源领域数据由目标领域数据线性表示,而且保持稀疏重构特性以及领域本身的结构。而Ham等[6]通过源领域和目标域数据集联合一起同时映射到一个共享的空间中,在这个空间中,来自不同数据集的对应点被设为同一个点。Lafon等[7]先用漫射方法将数据集嵌入低维空间,最后用仿射变换方法来对齐低维嵌入。Wang等[8]则提出了基于Procrustes分析的流形对齐方法,但仅将其应用于蛋白质分子对齐和跨语言信息检索。在遥感图像分类领域,Yang等[9]于2011年利用局部流形降维将2个遥感数据集同时映射到一个共享的流形空间进行一步对齐后采用K近邻分类的方法,但该算法需要有足够多的对应点; 2013年又提出了同时保持局部与全局几何结构的流形降维代替仅仅局部流形降维进行流形对齐的方法,虽然提高了性能却增加了算法的复杂度[10]。Tuia等[11]则充分利用源域和目标域的有标签数据点来构建相似图和不相似图,求解联合的拉普拉斯矩阵特征值分解,实现半监督流形对齐,扩展了流形对齐的应用范围,然而由于其算法采用标签对齐(可一对多或多对多)的方式,故不能实现精确的数据点和数据点之间的对齐。
本文采用基于Procrustes分析的流形对齐算法(Manifold alignment using procrustes analysis,MAPA),将其应用于多时相高光谱遥感图像分类。不同于上文中已在遥感领域用到的在流形降维中一步对齐的方法,本文的流形对齐算法分2步,首先对源域和目标域数据分别进行降维,然后再进行对齐,使得对齐后的2个域数据具有相同分布。因为在对齐过程中能得到显式的变换映射,所以该算法对新测试样本具有泛化能力。算法具体过程是先用一个标准的线性或非线性的降维方法将2个高光谱遥感数据集映射到低维(流形)空间中,再利用Procrustes分析方法将其低维嵌入之间的平移、旋转和缩放因子进行剔除,从而得到数据集间的最优对齐,最后用最近邻算法进行分类。
1 基于流形对齐的降维和分类算法
1.1 问题描述
流形对齐算法假设源域和目标域数据之间存在少量的对应点对,算法的目标是对2个域数据进行降维,使得降维后数据具有相同分布,从而可以找到这2个数据集中剩下的样本数据点之间的对应关系。假设目标域数据表示为

(1)
式中m为样本个数,源域数据表示为

(2)
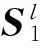
基于流形对齐的分类算法包括3个步骤: ①基于流形学习算法,分别将源域数据S1和目标域数据S2进行降维; ②利用Procrustes分析方法将这2个降维数据之间的平移、旋转和缩放因子进行剔除,从而可获得降维数据集间的最优对齐(使得降维数据具有同分布); ③对对齐后的降维数据采用最近邻分类算法对目标域数据进行分类。将原始数据变换到新的共享特征空间在第一和第二步中实现。第一步流形降维找到各自数据集的本真结构,第二步Procrustes分析进行对齐使得本真结构特征对齐,从而使新特征分布一致。
1.2 基于流形学习的数据降维
非线性降维是通过特征的非线性组合达到降维的目的,由于高光谱数据存在本质的非线性特性,所以非线性降维能更好地挖掘数据的非线性信息,提高后续图像分析的性能。对于线性化的流形学习,其计算简单,既能够保持数据局部结构,还具有泛化性能。因此,基于流形学习的数据降维对高光谱数据非常适用。
2000 年 Science 期刊上2篇流形学习文章的发表引领了流形学习算法研究的热潮,目前众多学者已经提出了多种不同的流形学习算法,以及这些算法的线性化和有监督形式的扩展。从几何形式来看,流形学习相当于将低维的流形结构嵌入到一个高维的欧氏空间中,所以也把这种映射称为嵌入映射。所谓的嵌入映射即相当于通过某种映射关系,把未知的、待求解的低维子空间中的流形嵌入到高维欧氏空间中。流形学习算法分为全局算法和局部算法,本文仅讨论局部算法。局部算法保持各相互重叠的局部结构内数据点之间的原有关系,对于不同的局部算法,其区别在于如何表述数据的局部结构,以及如何将各局部结构排列为一个整体流形结构(如何在低维流形中保持这些局部结构)。
流形学习算法都可以在图嵌入[12-13]框架下进行描述,不同的降维算法对应不同的拉普拉斯矩阵。设原数据为
S=[s1,…,sN]T∈RN×D,
(3)
式中:N为样本个数;D为数据维数,降维数据为
Z=[z1,…,zN]T∈RN×d,
(4)
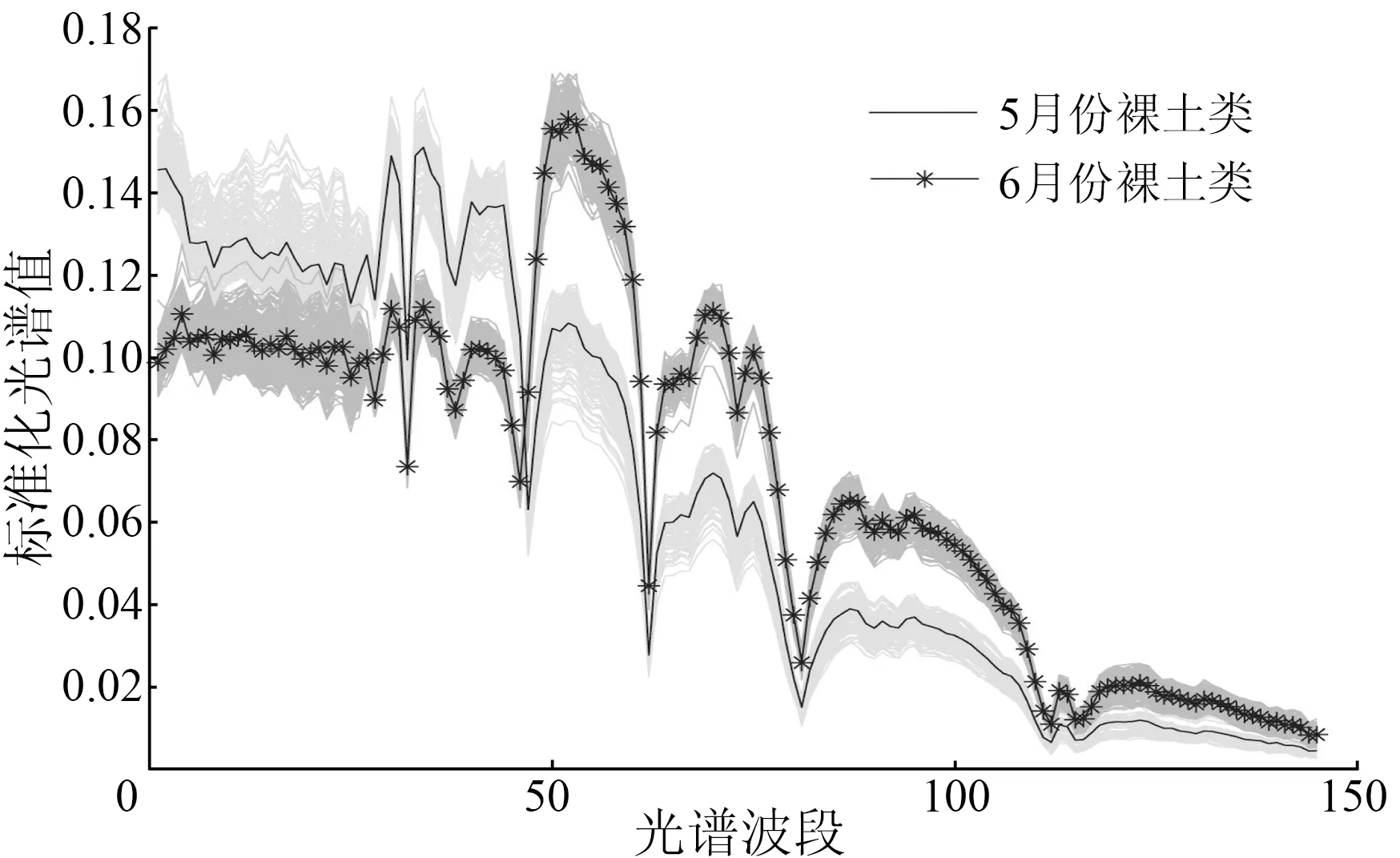
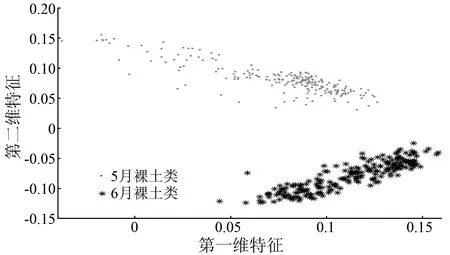
维数是d(d L=D-W, (5) 式中D为对角的程度矩阵, Dii=∑jWij,∀i。 (6) 图G的图嵌入定义为能够保持数据间相似性关系的最优低维数据表示,对于降至一维的情况(d=1),设流形坐标为z=[z1,z2,…,zN]T,目标函数为 (7) 式中m是常数,依赖于降维算法。可以看到,对于相似度高的点对(xi,xj),具有较大权值Wij,在此目标函数作用下,会使得降维数据(zi,zj)尽量接近。 该最优化问题可以转化为广义特征值分解问题,即 Lz=λDz。 (8) 降维结果z就是最小非零特征值对应的特征向量(最小的零特征值对应的特征向量为全1向量,舍去)。将一维情况扩展到多维目标函数,即 (9) 类似一维情况,d维流形坐标Z对应于最小的d个非零特征值对应的特征向量。 1.3 Procrustes分析 图像获取时间不同,其反映的植物长势、土壤条件、地形和光照条件等就可能不同,所以不同时间获取的源域和目标域高光谱数据可能具有不同的光谱特征。对于2个本质相似的高维数据集通过流形学习降维后,虽然保持了高维数据本真几何结构,但其低维嵌入间可能还存在旋转、平移和缩放等因素,可通过求得一个变换,使得2个域数据在变换后的特征空间,对应类别数据能够具有相似的特征,而Procrustes分析恰好能很好地解决这一问题。该分析是一种多元统计学中的形状比较分析方法,它试图寻找2组几何结构在旋转、平移、映像和缩放下的最佳逼近[14]。即通过固定某组结构,而对另外的结构选择进行合适的刚性变换,以估计2组结构之间的差别。因此,可以通过Procrustes分析直接比较2个本质相似的数据集的低维嵌入。 X=[x1,…,xn]T∈RN×d, (10) Y=[y1,…,yn]T∈RN×d。 (11) 首先固定X,然后对Y进行平移、缩放和旋转变换来匹配这2个结构,其结构差异为 (12) 式中‖·‖F是Frobenius范数。Procrustes算法的目的是将Y做线性变换,即 Y*=YΩ, (13) 式中Ω为线性变换矩阵,使得变换后的结构Y*和X具有最小的结构差异。 1.4 基于流形对齐的降维和分类算法的实现步骤 基于流形对齐的降维和分类算法,先用一个标准的线性或非线性的降维方法将2个高光谱遥感数据集映射到低维(流形)空间中,再利用Procrustes分析方法将其低维嵌入之间的平移、旋转和缩放因子进行剔除,从而得到数据集间的最优对齐,最后用最近邻法算法进行分类。 1.4.1 基于流形学习的数据降维 1) 假设S1和S2分别是目标域和源域数据集,分别对S1和S2中每个样本点xi和yi搜索其k个近邻点,近邻之间以边相连,构建邻域图。 2) 分别对S1和S2邻域图中相连的边计算权重矩阵W1和W2。权值可以设为1或者采用热核函数,即 (14) 1.4.2 用Procrustes分析寻找X和Y的最优对齐 1) 分别平移X,XU,Y和YU,使其中心在原点处。 2) 对YTX进行奇异值分解,即U∑VT=SVD(YTX)。 1.4.3 目标域分类 2.1 数据描述 不同时相高光谱遥感图像是迁移学习的一个典型应用场景。本文实验分别采用的是2001年5月、6月和7月在Okavango Delta, Botswana(BOT)地区采集的3幅Hyperion多时相高光谱遥感影像数据。该BOT遥感影像数据具有242个波段,光谱范围是357~2 576 nm,具有10 nm 的光谱分辨率和30 m的空间分辨率,去除未校准波段、噪声波段以及光谱重叠波段后剩余145个波段。该地区包括湿地和高地2个生态系统,3幅遥感影像具有9个相同的类别地物。实验人员在图像上获取了这9个类别的标记样本点数据,如表1所示。 表1 BOT影像标记样本数据数量 在3幅遥感影像中,由于卫星位置的变化,使得6月份和7月份数据包含了相同的地区,而5月份遥感影像和其他2个月份影像数据并不是精准的在同一地区位置。实验数据对由一个源域数据(5月份或6月份)和一个目标域数据(6月份或7月份)组成。因此,考虑到在空间和时间上光谱都漂移的情况,用5月/6月和6月/7月数据进行分类是更具挑战性的实验。光谱漂移以5月和6月的第9类裸土为例,如图1所示。 图1 5月和6月裸土类的光谱特征曲线比较 2.2 实验结果及分析 在实验中,把源域的带标签数据作为训练数据,把目标域的带标签样本作为测试数据,用来验证预测标签的正确性。实验分为3组,第一组是BOT数据5月影像(简称BOT5)和6月影像(简称BOT6)分别作为源域和目标域; 第二组为BOT5和BOT7分别作为源域和目标域; 第三组为BOT6和BOT7分别作为源域和目标域。基分类方法是对源域和目标域联合数据集通过降维方法,如主成分分析(principal component analysis,PCA)、局部保留投影(locality preserving projection,LPP)、拉普拉斯特征映射(laplacian eigenmaps,LE)和局部线性嵌入(locally linear embedding,LLE),学习流形后直接用K近邻分类,称为联合数据集流形学习(joint datasets manifold learning,JDML)算法。而本文算法MAPA是在流形降维后用Procrustes分析对齐,再用K近邻分类。 本文实验PCA,LPP,LE和LLE降维维度d选取范围为5︰5︰100,LPP和LE热核参数取值范围为0.25,0.5,0.75和1,构图近邻数k取值范围为5,7,9和11,LLE构图近邻数k取值范围为5︰5︰50,这些降维方法参数采用遍历法寻优。实验最后采用K近邻算法分类。因为是为了验证算法的有效性,所以对于K值并没有进行寻优,而取K=1。实验重复20次,对所有结果求平均值,作为算法的分类准确度。实验结果如表2—4所示。 表2 BOT5对BOT6分类结果比较 ①“-”表示JDML基分类算法用全部源域数据对目标域数据分类,即对应点比例不影响分类结果。表3和4中同此含义。 表3 BOT5对BOT7分类结果比较 表4 BOT6对BOT7分类结果比较 从表2—4中可分析得到,本文算法优于基分类方法,其中用LLE流形降维方法效果最好。随着先验信息给出的对应点数量增加,其准确率基本也随之增加,但如BOT5对BOT7用LPP和LE来流形对齐时并没有一直增加,这是因为先验给出的对应点是人工给出的,所以为了满足对应点数量上的要求,把实际上对应不是很好的点强制匹配,从而导致分类精度有所下降。在BOT6对BOT7的流形对齐方法比基分类方法提升的并不是很多,是由于这2幅影像覆盖的地区完全一样只有时间上的变化,从而导致的光谱漂移并不大,因此,当选择降维效果更好的LLE方法时,基分类器效果略高一点。 为体现原始数据特征经本文算法变换后特征分布是否一致,以5月和6月中的第9类裸土类为例,为直观反应原始数据特征分布,降维方法使用PCA。图2和图3对比了原始数据流形降维特征分布和流形对齐后新的特征分布,可以看出,在原始数据流形降维特征分布中,特征分布有一定的漂移,但经过本文流形对齐算法后新的特征分布变得一致。 图2 5月和6月原始数据裸土类流形降维特征分布 图3 5月和6月原始数据裸土类流形对齐特征分布 为体现本文算法的优势,对比了在高光谱遥感领域适应性分类研究已有的经典一步流形对齐算法。Yang等[9]的半监督联合流形对齐(semisupervised jonit manifold alignment,SJMA)算法和Tuia 等[11]的半监督流形对齐(semisupervised manifold alignment,SSMA)算法。实验流形降维方法采用论文中用到的LPP,对应点比例取5%,其他参数设置和上述实验中相同。实验结果如表5所示。 表5 BOT数据集的分类结果比较 分析表5可知,在对应点比较少只有5%的情况下,在实验数据组中MAPA方法分类准确率都优于SJMA和SSMA算法。这是因为相对于SJMA算法,本文MAPA算法的优势在于更适用于先验信息少的情况,对于减少人工参与是非常有意义的。对于SSMA算法,先验信息表现为源域和目标域数据的标签信息,由于源域和目标域的每个类别包含多个标签数据点,因此,SSMA采用标签对齐,可一对多或多对多的对齐方式,不能实现精确的数据点和数据点之间的对齐; 而本文MAPA算法利用对应点先验信息,使得数据点对之间实现一对一的对齐,具有更好的迁移学习效果。 针对多时相高光谱遥感图像中光谱漂移造成的分类困难,本文采用了一种基于流形对齐的域适应分类算法,利用数据集间相似的本真几何结构特性,先用线性或非线性降维算法将数据集映射到低维空间,然后用Procrustes分析法移除平移、旋转和缩放因子后得到低维嵌入的最优对齐,最后用最近邻法算法进行分类。实验表明,在光谱特征相似但分布不同的多时相高光谱遥感数据分类中,本文算法优于对联合数据集直接流形学习降维后用K近邻进行分类的JDML算法,而且对比了几种降维方法,其中LLE优于PCA,LPP和LE 降维后对齐的结果,同时,在对应点比例比较少的情况下,本文算法优于经典的一步流形对齐SJMA和SSMA算法。因此,探索优秀的降维算法将是下一步的研究内容。 [1] Wang C.A Geometric Framework For Transfer Learning Using Manifold Alignment[D].Amherst,Massachusetts:University of Massachusetts Amherst,2010. [2] Pan S J,Kwok J T,Yang Q.Transfer learning via dimensionality reduction[C]//Fox D,Gomes C P.Proceedings of the 23rd Conference on Artificial Intelligence.Chicago:AAAI Press,2008:677-682. [3] Gu Q Q,Zhou J.Learning the shared subspace for multi-task clustering and transductive transfer classification[C]//Proceedings of the Ninth IEEE international conference on data mining.Miami,FL:IEEE,2009:159-168. [4] Blitzer J,McDonald R,Pereira F.Domain adaptation with structural correspondence learning[C]//Proceedings of the 2006 Conference on Empirical Methods in Natural Language Processing.Stroudsburg,PA,USA:Association for Computational Linguistics,2006:120-128. [5] Kan M N,Wu J T,Shan S G,et al.Domain adaptation for face recognition:Targetize source domain bridged by common subspace[J].International Journal of Computer Vision,2014,109(1/2):94-109. [6] Ham J,Lee D D,Saul L K.Semisupervised alignment of manifolds[C]//Ghahramani Z,Cowell R.Proceedings of the Annual Conference on Uncertainty in Artificial Intelligence. Edinburgh,Scotland,UK:UAI,2005,10:120-127. [7] Lafon S,Keller Y,Coifman R R.Data fusion and multicue data matching by diffusion maps[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2006,28(11):1784-1797. [8] Wang C,Mahadevan S.Manifold alignment using Procrustes analysis[C]//Proceedings of the 25th International Conference on Machine Learning.New York,NY,USA:ACM,2008:1120-1127. [9] Yang H L,Crawford M M.Manifold alignment for multitemporal hyperspectral image classification[C]//Proceedings of 2011 IEEE International Geoscience and Remote Sensing Symposium(IGARSS).Vancouver,BC,Canada:IEEE,2011:4332-4335. [10]Yang H L,Crawford M M.Learning a joint manifold with global-local preservation for multitemporal hyperspectral image classification[C]//Proceedings of 2013 IEEE International Geoscience and Remote Sensing Symposium(IGARSS).Melbourne,Australia:IEEE,2013:1047-1050. [11]Tuia D,Volpi M,Trolliet M,et al.Semisupervised manifold alignment of multimodal remote sensing images[J].IEEE Transactions on Geoscience and Remote Sensing,2014,52(12):7708-7720. [12]Yan S C,Xu D,Zhang B Y,et al.Graph embedding and extensions:A general framework for dimensionality reduction[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2007,29(1):40-51. [13]Yan S C,Xu D,Zhang B Y,et al.Graph embedding:A general framework for dimensionality reduction[C]//Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition.San Diego,CA,USA:IEEE,2005,2:830-837. [14]Sibson R.Studies in the robustness of multidimensional scaling:Procrustes statistics[J].Journal of the Royal Statistical Society.Series B(Methodological),1978,40(2):234-238. (责任编辑: 李瑜) Manifold alignment for dimension reduction and classification of multitemporal hyperspectral image LU Jintao, MA Li (SchoolofMechanicalEngineeringandElectronicInformation,ChinaUniversityofGeosciences(Wuhan),Wuhan430074,China) For multitemporal hyperspectral images, the spectral characteristics of the same land cover object may vary significantly. Therefore, manifold alignment algorithm was employed to find a feature space in which data distributions of both images become the same. The method includes three steps. Firstly, a standard linear or nonlinear dimension reduction method is used to reduce the dimensionality of hyperspectral images. Secondly, the Procrustes analysis method is utilized to remove the translational, rotational and scaling components from one set so that the optimal alignment between the two data sets can be achieved. Finally, the nearest neighbor algorithm is applied for classification. Experimental results using multitemporal hyperion images demonstrate that the proposed approach can obtain performances which are superior to those of several popular manifold alignment methods. Procrustes; manifold alignment; multitemporal; hyperspectral image; dimension reduction; classification 10.6046/gtzyyg.2017.01.16 鲁锦涛,马丽.基于流形对齐的高光谱遥感图像降维和分类算法[J].国土资源遥感,2017,29(1):104-109.(Lu J T,Ma L.Manifold alignment for dimension reduction and classification of multitemporal hyperspectral image[J].Remote Sensing for Land and Resources,2017,29(1):104-109.) 2015-09-14; 2016-02-18 国家自然科学基金项目“基于流形学习进行图结构设计的高光谱图像分类技术研究”(编号: 61102104)资助。 鲁锦涛(1990-),男,硕士研究生,主要从事图像处理和机器学习等方面的研究。Email: lujintao2016@163.com。 马丽(1982-),女,讲师,博士,主要从事遥感影像分析、计算机视觉和机器学习等方面的研究。Email: maryparisster@gmail.com。 TP 751.1 A 1001-070X(2017)01-0104-06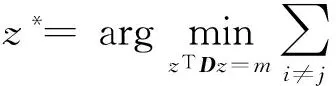
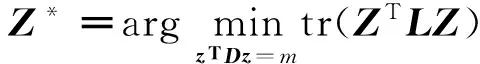
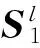
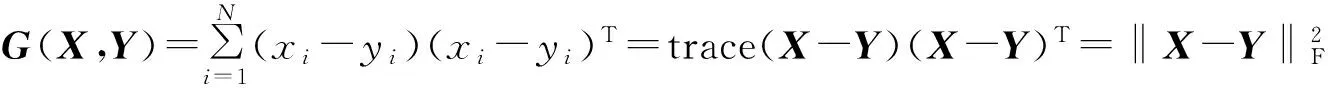
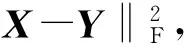
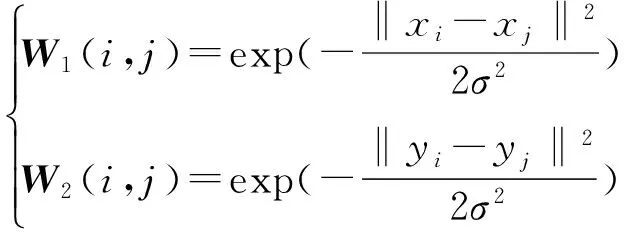
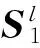
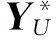
2 实验结果与分析





3 结论
