基于Hapke模型混合岩矿粉末反射率光谱模拟

王喆， 赵哲， 闫柏琨， 杨苏明

(1.中国国土资源航空物探遥感中心，北京 100083； 2.河北省煤田地质局，石家庄 050085)

基于Hapke模型混合岩矿粉末反射率光谱模拟

王喆1， 赵哲2， 闫柏琨1， 杨苏明1

(1.中国国土资源航空物探遥感中心，北京 100083； 2.河北省煤田地质局，石家庄 050085)

Hapke岩矿二向反射率光谱定量模型是研究混合矿物光谱的有利工具，而国内对该模型的基础研究较少。通过4组室内混合矿物光谱数据来研究该模型在模拟混合矿物光谱时的准确性与存在的问题，进而探讨混合矿物光谱的特征规律。研究表明，在模拟混合矿物光谱方面不论是各向同性，还是各向异性的Hapke模型均有很高的精度，权重调整后4组各向同性模型的模拟结果均方根误差(RMSE)均值为0.014 4，相关系数(R)均值为0.994 7，4组各向异性模型的模拟结果RMSE均值为0.008 4，R均值为0.994 4，说明该模型是优异的混合光谱分析手段； 但模型对暗色矿物适用性较差，如当混合矿物中含有黑云母时模拟精度较低； 混合矿物的光谱谱形需要针对矿物组成进行具体分析，其中所占质量分数较高的矿物并不一定能主导混合矿物的光谱谱形，而低反射率的矿物在混合矿物光谱中发挥的作用远大于其质量分数的比重。

Hapke模型； 混合光谱； 反射光谱； 模拟光谱； 矿物

0 引言

可见光-近红外波段(0.4～2.5μm)是研究地球表面矿物组成和含量的重要波段范围，随着高光谱技术逐渐普及，在该波段区间可获取更加丰富的土壤、岩石理化等信息。由于传感器空间分辨率的限制以及自然界地物的复杂多样性，混合像元普遍存在于遥感图像中[1]。裸露地表也多是由不同类型土壤和矿物等混合而成[2]。混合矿物光谱通常是非线性混合的，并且非常复杂[3]。如何提升对混合光谱的认识，研究混合矿物光谱的规律，以便更好地分析地物光谱特征是遥感人员需要面对的问题。

作为研究混合矿物光谱的有利工具，Hapke岩矿二向反射率光谱模型[4-5](简称Hapke模型)是以Chandrassekhar辐射传输理论[6]为基础，考虑了多次散射和粒子相互阴影效应的用于行星表面风化土体光散射特性研究的二向性反射模型[7]。其主要用途为： ①通过光谱模拟作为影像标准参考光谱或进行图像光学校正； ②混合光谱解混，估算矿物组成和丰度； ③推测土体表面物理性质[8-9]。混合矿物二向反射率光谱模拟为Hapke模型的正用方式(forward model)，而后2点利用该模型进行矿物丰度等方面的定量分析则属于逆用方式(inverse model)。虽然正用方式是逆用方式的基础，但在实际应用中常侧重后2点的作用而忽视了该模型在模拟混合矿物光谱方面的优势。Li等[10]对月壤样品反射率光谱开展了模拟，结果表明模拟光谱和实测光谱相关系数优于0.99，均方根误差(root mean square errors,RMSE)最大为0.008 49； Mustard等[11]对月壤常见矿物的混合光谱进行模拟，结果显示模拟光谱与真实光谱误差在7%以内； Cheek等[12]对月壤常见矿物进行两两混合测试，结果表明模拟光谱中含有橄榄石的一组误差大于10%。从以上前人研究结果可以看出，虽然该模型应用范围较广，但对模型模拟精度与可靠性的研究较少，研究结果也存在一定分歧，且多以行星表面矿物为研究对象[8-10]。行星表面矿物与地表常见矿物有较大差异，如月壤主要矿物以橄榄石、辉石、斜长石、钛铁矿和熔融玻璃为主[13]。

基于上述思考，本文以石英、斜长石、黑云母、辉石、橄榄石和透闪石等地表常见矿物粉末样品为研究对象，主要针对Hapke模型在模拟混合矿物光谱方面的准确性进行研究。在实验室中通过对多组混合矿物反射率光谱进行测试，采用Hapke各向同性模型(IMSA)和各向异性模型(AMSA)分别对混合矿物光谱进行模拟及评价。从而加深对该模型参数的理解，掌握其在模拟地表混合矿物光谱方面的优势与不足，为混合光谱研究提供理论依据。

1 Hapke模型

1.1 Hapke IMSA和AMSA模型参数

Hapke模型由Hapke于1981年首次提出，其原始模型为各向同性多次散射近似Hapke模型，其多次散射部分是基于粒子表面反射各向同性的假设； 2002年Hapke模型对多次散射部分采用各向异性多次散射近似解[14-15]，考虑了颗粒各向异性对光散射的影响，从而提高了多次散射部分的模拟精度。但是，IMSI模型中散射相函数(p(g))为1，后向效应函数(B(g))经常被忽略或简化，因此IMSA模型公式要比AMSA模型公式简化许多。基于Hapke IMSA和AMSA模型矿物反射率r(i,e,g)的表达式分别为

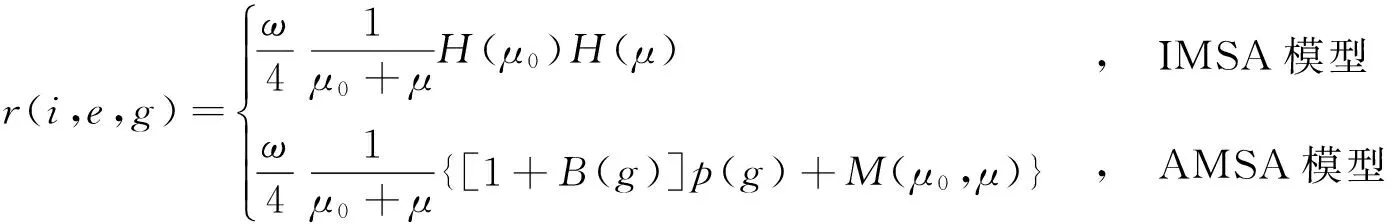
(1)

式中：i,e和g分别表示入射光天顶角、出射光天顶角和相位角，如图1所示。

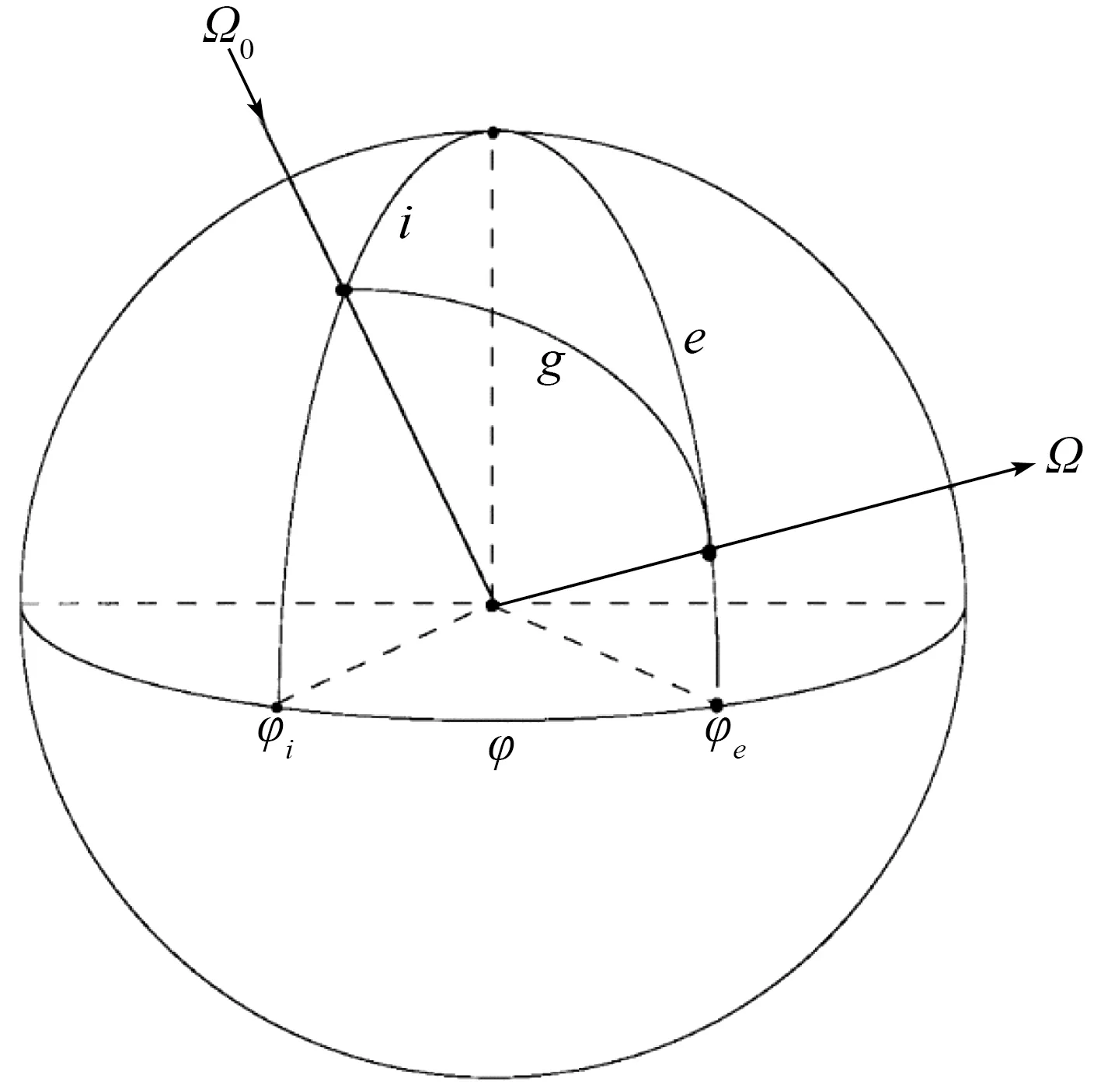
图1 双向反射几何原理

ω表示单次散射反照率(average single-scattering albedo)；μ0=cosi；μ=cose；H(x)为计算颗粒多次散射部分的函数，在AMSA模型中做出了改进，表现为更接近辐射传输方程精确解的近似表达式，即

(2)

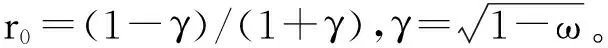
B(g)表示后向散射函数(backscatterfunction)，代表后向效应对光谱的作用，后向效应主要用于描述小相位角时传感器接收反射能量出现非线性增加的现象[16]，其为后向效应宽度h、相位角g以及后向效应振幅B0的函数，即

B(g)=B0/[1+(1/h)tan(g/2)]。

(3)

p(g)是单次散射相函数(phasefunction)，用来描述散射能量在不同方位角的分布规律，反映了颗粒散射特性。依据物质表面的特性，相函数通常符合各向同性散射、前向散射和后向散射。其表达式经常采用一阶或二阶勒让德多项式或单参数、双参数Henyey-Greenstein函数表示，本文采用二阶勒让德多项式拟合函数，计算公式为

(4)

M(μ0,μ)是AMSA模型中新引入的计算多次散射的函数，具体表达式参见文献[14]。

1.2 混合矿物光谱模拟与评价方法

由于ω表征一束光线照射到单个矿物颗粒表面时散射能量与入射能量之比，不包含多次散射辐射，遵循线性混合规律[17]。求解混合矿物光谱反射率时，需要先求解出每个矿物端元的ω，之后带入式(5)，即

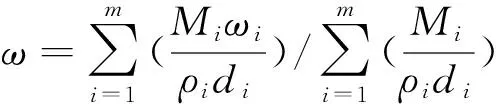
(5)

式中： Mi,ωi,ρi和di分别为第i种矿物质量分数、单次散射反照率、密度和平均粒径； m为混合矿物中矿物种数。

混合矿物光谱模拟结果与实测结果采用RMSE和相关系数(R)进行评价，用以确定模型模拟结果的准确性。

RMSE是用来衡量观测值同真值之间的偏差。公式为

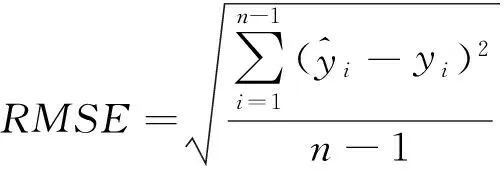
(6)

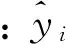
R是用以反映变量之间相关关系密切程度的统计指标。公式为

(7)

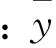
2 材料和实验

2.1 岩矿粉末样品准备

为了测试Hapke模型对混合矿物反射率光谱模拟的准确性，针对地球表面常见矿物，选取实验室中4组比例不同、矿物成分不同的混合样品进行测试(表1)。4组混合矿物使用不同的矿物组合、质量分数、粒径和矿物组成数，有利于更准确、全面客观地评价该模型的模拟结果。

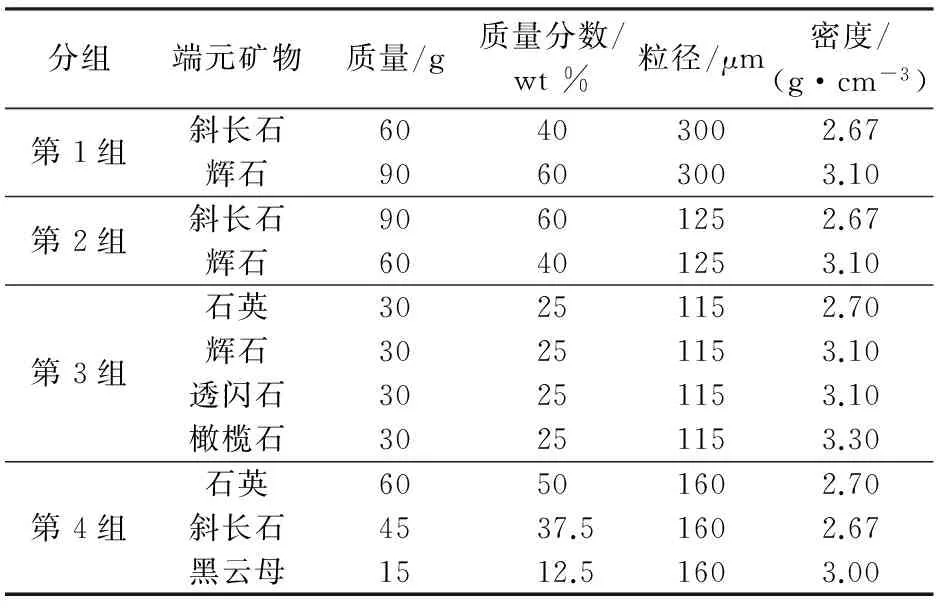
表1 各组矿物端元组成

由式(5)可知，模型中矿物混合需要使用质量分数计算，根据选取好的混合矿物组成，使用天平秤对矿物颗粒质量进行精准称量，并放入器皿中充分混合摇匀。之后装入半径为4 cm，深为2 cm的深色容器中，以消除容器过浅对矿物光谱波动性和离散性的影响[18]。最后使用直尺轻轻将样品表面刮平，保证样品表面足够平整。

2.2 室内岩矿粉末样品二向反射率光谱测定

在实验室黑暗环境中，使用美国ASD FieldSpec FR Pro便携式分光辐射光谱仪对岩矿粉末二向反射率光谱进行测量。在实验室光谱数据采集时，需要同时测量白板和岩矿样品反射辐射。白板由硫酸钡(BaSO4)等材料压制或烧制而成，当观测天顶角小于45°时接近朗伯体，其性能稳定、表面均匀，具有各向同性[19]。将矿物样品水平置于光学角度自动调整仪上(图2)，25°视场角探头距样品表面垂直距离为12 cm，50 W卤光灯距离样品表面直线距离为40 cm。光学角度自动调整仪可通过软件操作对各光学角度进行精确调整，最大程度保证光源天顶角、探头天顶角和方位角的准确性。由于本次光谱采集不涉及多种光学角度的二向反射率问题，因此仅设定1组角度： 入射光天顶角为30°，探头天顶角为0°。每组混合矿物光谱数据均采集5次，对5组数据取均值以减少误差。由于光谱仪存在噪声，需将光谱重采样至0.4～2.25 μm之间。

图2 光学角度自动调整仪

3 结果和分析

3.1 混合矿物反射率光谱模拟结果

分别采用Hapke IMSA和AMSA模型对4组混合矿物的二向反射率进行模拟。为更加直观展现混合矿物光谱非线性混合的特性，在对比结果中加入按照质量分数进行线性混合的模拟反射率光谱曲线。并利用RMSE和相关系数为(R) 2个指数进行评价，误差统计结果如表2所示。模拟结果如图3所示。

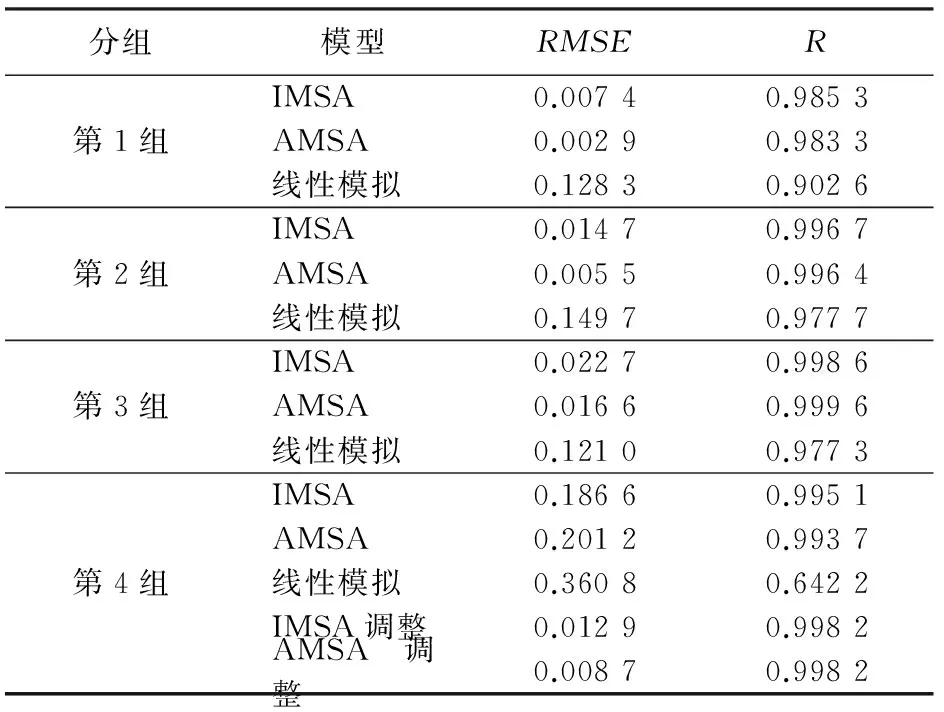
表2 模拟结果误差统计

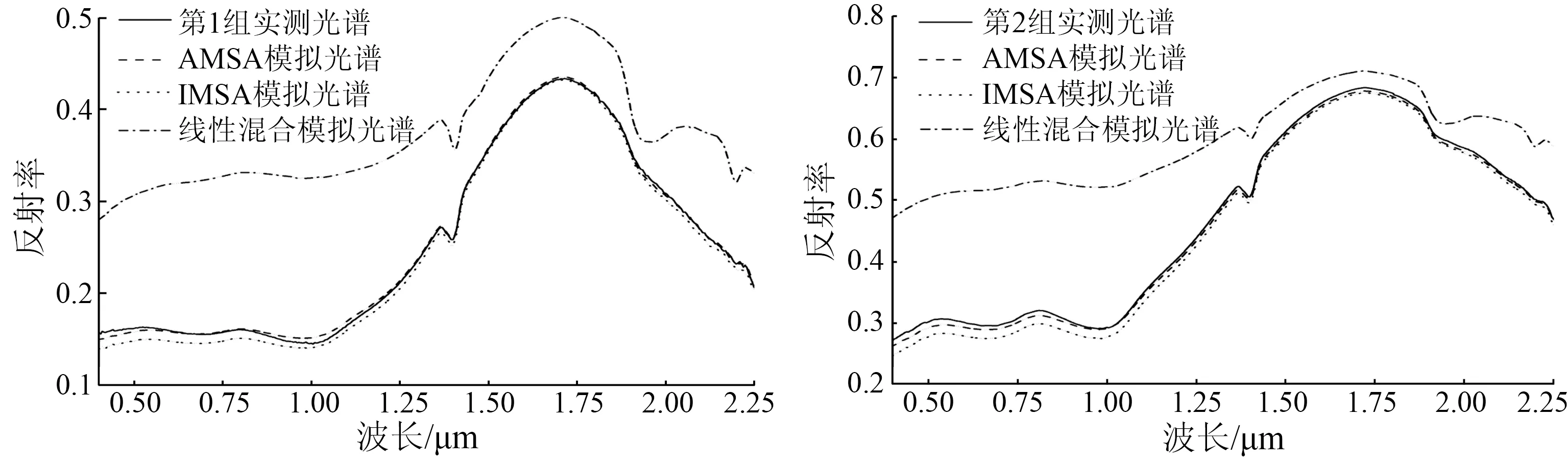
(a) 第1组 (b) 第2组

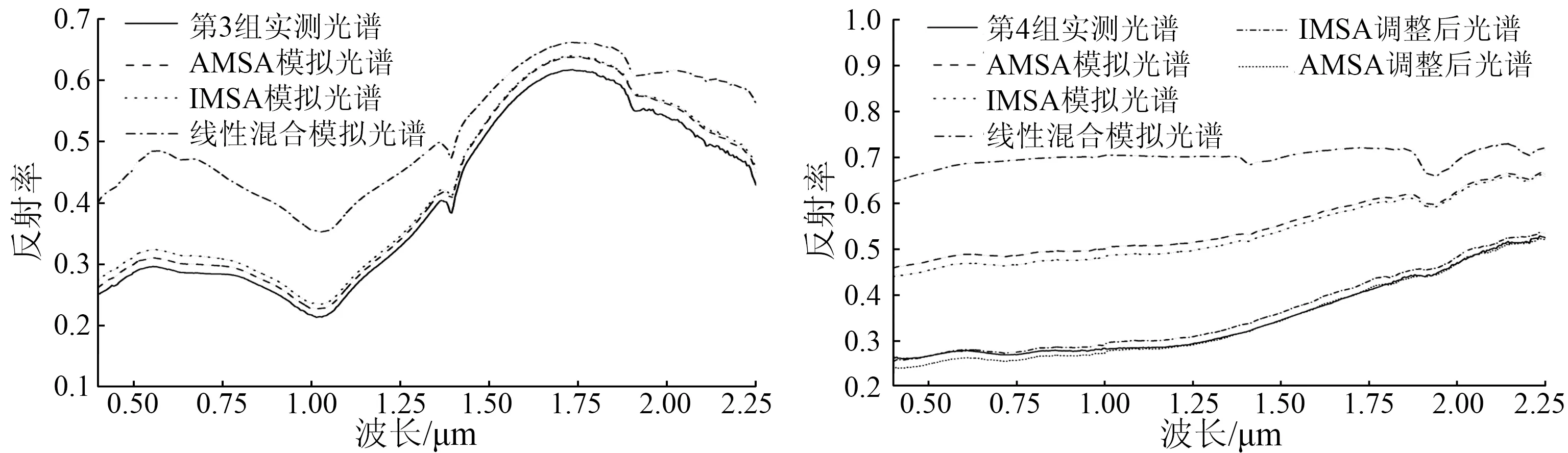
(c) 第3组 (d) 第4组

图3 4组混合矿物模拟结果对比

Fig.3 Four groups of simulation results

从表2和图3中可以看出，与线性混合模拟结果相比，IMSA与AMSA模型在4组模拟结果中均具有较高的精度。其中，前3组IMSA模型模拟结果的RMSE和R均值分别为0.014 9和0.993 5，前3组AMSA模型模拟结果的RMSE和R均值分别为0.008 3和0.993 1，模拟精度极高。而第4组模拟精度明显低于前3组数据，主要原因在于混合矿物中加入了黑云母，而Hapke模型中ω仅对透明矿物(折射系数虚部k<<1)适用性良好[20]，因此混合矿物中含有暗色矿物会降低模拟精度，黑云母是片状矿物也可能是导致误差较大的原因之一。但研究中发现只需调整黑云母在式(5)中的权重值，即可提升模型模拟的精度，可见模型低估了不透明矿物的作用。黑云母权重调整后IMSA和AMSA模型RMSE和R均值分别为0.010 8和0.998 2，模拟精度较之前有了很大提升。通过以上结果可知： ①虽然Hapke AMSA模型比IMSA模型复杂很多，但在模拟单一角度混合矿物反射率光谱时，2种模型模拟结果差异很小，选择IMSA模型可大大简化计算量。但应注意到，当涉及到多种角度的二向反射率模拟时，AMSA模型的模拟精度会更高； ②Hapke模型对黑云母(不透明矿物)的模拟结果并不理想，后续研究应着重解决此问题以提升模型对暗色矿物的模拟精度； ③Hapke模型在模拟混合矿物反射率光谱方面准确性非常高，其模拟结果具有很高的参考价值。

3.2 混合矿物反射率光谱特征分析

以第1组和第2组混合矿物为例(表1)，第1组混合矿物中斜长石为40 wt%，辉石为60 wt%，第2组混合矿物中斜长石提升为60 wt%，辉石降低为40 wt%。从图4中可以看出，不论斜长石质量分数为40 wt%或60 wt%，混合矿物反射率光谱都与辉石谱形极为相似，只是混合矿物反射率略高于辉石反射率，仿佛斜长石并没有在混合矿物光谱中发挥作用似的。

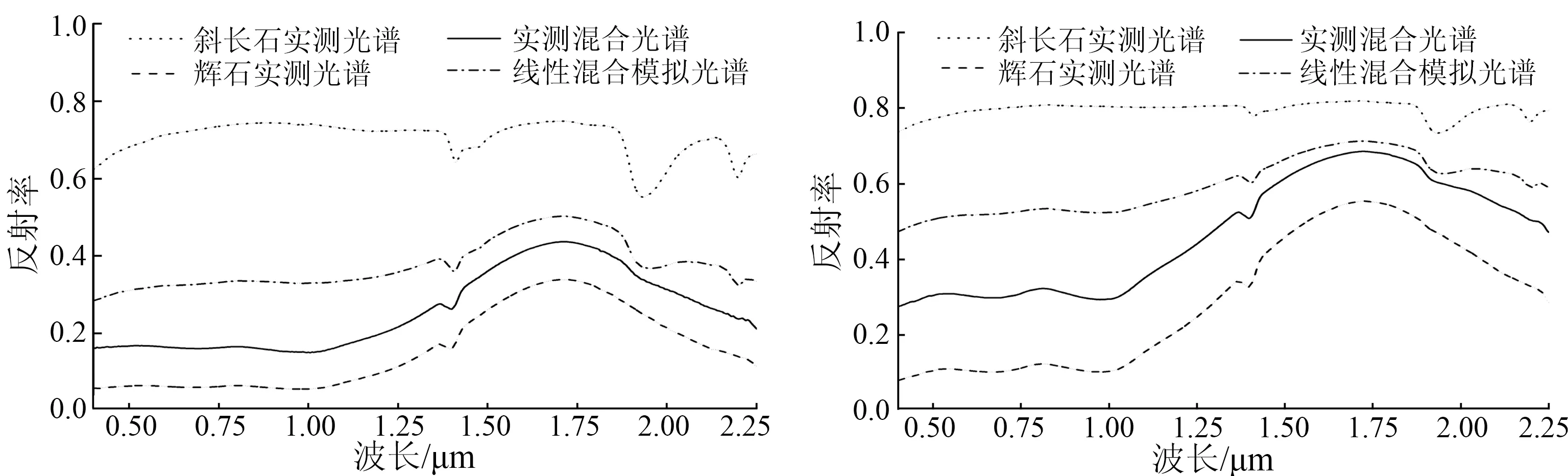
(a) 第1组 (b) 第2组

图4 斜长石与辉石以2种不同比例混合而成的矿物反射率光谱对比

Fig.4 Plagioclase and pyroxene and their mixed bidirectional reflectance spectra

从图4中可知，斜长石在1.9 μm和2.2 μm处均有非常明显的吸收特征，但在实测的混合光谱中并没有明显的体现。人们主观判断混合矿物光谱往往与线性混合结果非常相似，常常认为由于斜长石在1.9 μm和2.2 μm有吸收特征，在混合光谱中也一定会有明显的吸收特征，但图4真实混合光谱与线性混合光谱存在着很大差异。斜长石与辉石在1.4 μm处均有显著吸收特征，混合光谱在该波段处并没有因为2种矿物均有吸收而有所加强。以上结果表明： ①混合矿物的光谱是非线性的，简单以质量分数进行线性混合的结果与真实反射率差异很大，不能用惯性的线性思维去思考； ②某一矿物在某一波段有强烈吸收，并不一定会对混合矿物光谱造成吸收特征； ③多种矿物在某一波段均有明显吸收特征，并不表示混合矿物光谱在此处吸收特征会增强，至于是哪种矿物主导该处的吸收或反射特征，需要进行深入分析； ④在混合矿物光谱中，质量分数占有较高权重的矿物并不一定能主导混合矿物的光谱谱形，应针对混合矿物组成、含量等进行具体分析； ⑤混合矿物中低反射率的矿物所发挥的作用远大于其质量分数的比重，具体原因仍有待深入研究。

4 结论

针对地表常见矿物，在实验室内对4组混合矿物二向反射率光谱进行测定，采用Hapke模型对混合矿物反射率光谱进行模拟，通过均方根误差RMSE和相关系数R对模拟结果进行评价，得出以下结论：

1)Hapke模型在模拟混合矿物反射率光谱方面具有很高的精度，虽然AMSA模型模拟准确性略高于IMSA模型，但采用IMSA模型可简化计算量，提升计算效率。

2)当混合矿物中含有黑云母时，模型模拟精度较低，表明该模型对暗色矿物适用性较差。

3)混合矿物反射率光谱是非线性混合的，光谱的吸收谷与反射峰位置需要针对矿物组成和含量进行具体分析，质量分数所占较高的矿物并不一定能主导混合矿物的光谱谱形，低反射率的矿物在混合矿物光谱中所发挥的作用大于其质量分数的比重。

本文对Hapke模型在模拟混合矿物反射率光谱方面进行了初步研究，但实验中仍存在一些不足，如仪器噪声、模拟的矿物种类较少、仅有黑云母一种低反射率片状矿物等。未来研究将进一步改进模型，以提升其在模拟含有黑云母等暗色矿物的混合矿物光谱时的准确性。

[1] 代晶晶,李庆亭.基于Hapke和Shkuratov模型的斑岩铜矿蚀变带混合波谱研究[J].地质与勘探,2013,49(3):505-510. Dai J J,Li Q T.Study on mixed spectra of alteration zones in porphyry copper deposits based on the Hapke and Shkuratov models[J].Geology and Exploration,2013,49(3):505-510.

[2] Foody G M,Cox D P.Sub-pixel land cover composition estimation using a linear mixture model and fuzzy membership functions[J].International Journal of Remote Sensing,1994,15(3):619-631.

[3] Clark R N,Swayze G A,Livo K E,et al.Imaging spectroscopy:Earth and planetary remote sensing with the USGS Tetracorder and expert systems[J].Journal of Geophysical Research,2003,108(E12):5131.

[4] Hapke B.Bidirectional reflectance spectroscopy:1.Theory[J].Journal of Geophysical Research,1981,86(B4):3039-3054.

[5] Hapke B,Wells E.Bidirectional reflectance spectroscopy:2.Experiments and observations[J].Journal of Geophysical Research,1981,86(B4):3055-3060.

[6] Chandrasekhar S.Radiative Transfer[M].New York:Dover Publications,1960.

[7] 徐元柳.基于裸露地表辐射传输模型的粗糙度反演与地形校正[D].北京:中国地质大学(北京),2009. Xu Y L.Roughness Retrieval and Topographic Correction Based on Bare Surface Radiative Transfer Model[D].Beijing:China University of Geosciences(Beijing),2009.

[8] Shepard M K,Helfenstein P.A test of the Hapke photometric model[J].Journal of Geophysical Research,2007,112(E3):E03001.

[9] Ciarniello M,Capaccioni F,Filacchione G,et al.Hapke modeling of Rhea surface properties through Cassini-VIMS spectra[J].Icarus,2011,214(2):541-555.

[10]Li S,Li L.Radiative transfer modeling for quantifying lunar surface minerals,particle size,and submicroscopic metallic Fe[J].Journal of Geophysical Research,2011,116(E9):E09001.

[11]Mustard J F,Pieters C M.Photometric phase functions of common geologic minerals and applications to quantitative analysis of mineral mixture reflectance spectra[J].Journal of Geophysical Research,1989,94(B10):13619-13634.

[12]Cheek L C,Pieters C M.Reflectance spectroscopy of plagioclase-dominated mineral mixtures:Implications for characterizing lunar anorthosites remotely[J].American Mineralogist,2014,99(10):1871-1892.

[13]Papike J J,Simon S B,Laul J C.The lunar regolith:Chemistry,mineralogy,and petrology[J].Reviews of Geophysics,1982,20(4):761-826.

[14]Hapke B.Bidirectional reflectance spectroscopy:5.The coherent backscatter opposition effect and anisotropic scattering[J].Icarus,2002,157(2):523-534.

[15]Hapke B.Theory of Reflectance and Emittance Spectroscopy[M].New York:Cambridge University Press,2005.

[16]陈明.基于分形理论的岩矿光谱模型研究[D].武汉:华中科技大学,2010. Chen M.Study on the Spectral Model of Rocks and Minerals Based on Fractal[D].Wuhan:Huazhong University of Science and Technology,2010.

[17]闫柏琨,李建忠,甘甫平,等.一种月壤主要矿物组分含量反演的光谱解混方法[J].光谱学与光谱分析,2012,32(12):3335-3340. Yan B K,Li J Z,Gan F P,et al.A spectral unmixing method of estimating main minerals abundance of lunar soils[J].Spectroscopy and Spectral Analysis,2012,32(12):3335-3340.

[18]程街亮,史舟,李洪义.不同类型土壤的二向反射光谱特性及模拟[J].光谱学与光谱分析,2008,28(5):1007-1011. Cheng J L,Shi Z,Li H Y.Observation and simulation of bi-directional spectral reflectance on different type of soils[J].Spectroscopy and Spectral Analysis,2008,28(5):1007-1011.

[19]田丰.全波段(0.35～25μm)高光谱遥感矿物识别和定量化反演技术研究[D].北京:中国地质大学(北京),2010. Tian F.Identification and Quantitative Retrival of Minerals Information Integrating VIS-NIR-MIR-TIR(0.35～25μm) Hyspectral Data[D].Beijing:China University of Geosciences(Beijing),2010.

[20]Lemelin M,Morisset C E,Germain M,et al.Ilmenite mapping of the lunar regolith over mare australe and mare ingenii regions:An optimized multisource approach based on Hapke radiative transfer theory[J].Journal of Geophysical Research:Planets,2013,118(2):2582-2593.

(责任编辑： 陈理)

Simulation of bi-directional reflectance on mixed minerals based on Hapke photometric model

WANG Zhe1, ZHAO Zhe2, YAN Bokun1, YANG Suming1

(1.ChinaAeroGeophysicalSurveyandRemoteSensingCenterforLandandResources,Beijing100083,China;2.HebeiBureauofCoalGeologicalExploration,Shijiazhuang050085,China)

Hapke photometric model is a useful tool for studying the spectra of mixed minerals. However, there are still some improvable things, and domestic research still lags far behind that of foreign countries. This paper focuses on the characteristics of surface minerals through 4 groups of spectroscopic tests in laboratory, and then discusses and points out the accuracy of the Hapke photometric model when simulating the spectra of mixed minerals. The mean of root mean square errors (RMSE) of the 4 groups by using IMSA model is 0.014 4, and the mean of correlation coefficients (R) is 0.994 7. The mean ofRMSEof the 4 groups by using AMSA model is 0.008 4, and the mean ofRis 0.994 4. These data suggest that IMSA model and AMSA model have a very high precision and can be a good means to simulate spectral mixture of mixed minerals. Nevertheless, the experiment results show that, when the mixed minerals contain biotite, the accuracy is not satisfactory, but the accuracy of simulation can be improved by adjusting the weight of biotite. Spectral shape of mixed minerals needs a specific analysis of compositions of the mixed mineral, for instance, a particular mineral which possesses a higher mass fraction in the mixed minerals may not play the leading role in the spectral shape, while the mineral of low reflectivity may play a more important role.

Hapke model; mixed spectra; reflectance spectra; simulation spectra; mineral

10.6046/gtzyyg.2017.01.28

王喆,赵哲,闫柏琨,等.基于Hapke模型混合岩矿粉末反射率光谱模拟[J].国土资源遥感,2017,29(1):186-191.(Wang Z,Zhao Z,Yan B K,et al.Simulation of bi-directional reflectance on mixed minerals based on Hapke photometric model[J].Remote Sensing for Land and Resources,2017,29(1):186-191.)

2015-09-08；

2015-11-03

中国地质调查局地质调查项目“高光谱地质调查技术方法研究”(编号： 12120115040801)资助。

王喆(1989- ),助理工程师,主要从事遥感地质应用研究。Email： wangzhe_cnbj@163.com。

闫柏琨(1977- ),博士,高级工程师,主要从事高光谱与遥感地质应用研究。Email： yanbokun_2006@yahoo.com.cn。

TP 79

A

1001-070X(2017)01-0186-06