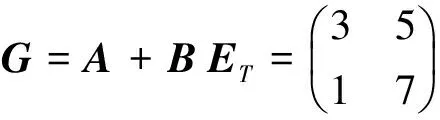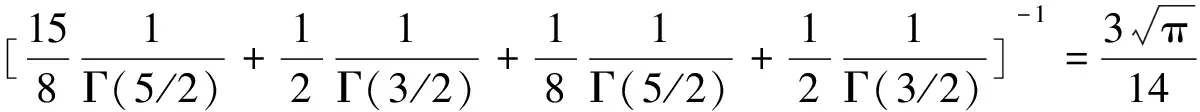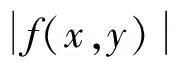Caputo型分数阶微分方程边值问题解的存在唯一性
2017-04-17张淑琴
杨 帅, 张淑琴
(1.中国矿业大学(北京) 力学与建筑工程学院 北京 100083; 2.中国矿业大学(北京) 理学院 北京 100083)
Caputo型分数阶微分方程边值问题解的存在唯一性
杨 帅1, 张淑琴2
(1.中国矿业大学(北京) 力学与建筑工程学院 北京 100083; 2.中国矿业大学(北京) 理学院 北京 100083)
主要探讨一类Caputo型分数阶微分方程边值问题解的存在唯一性. 通过将边值问题转化为等价的Fredholm积分方程,在巴拿赫空间上运用不动点定理,证明了积分方程解的存在性和唯一性.
Caputo型分数阶微分方程; 边值问题; Fredholm积分方程; 不动点
0 引言
分数阶微分方程已经广泛应用于分数物理学、分子动力学、自动控制、电化学等各个科学研究领域[1-3].关于分数阶微分方程的边值问题也一直是分数阶微积分理论的一个重要研究课题,其在模拟工程、物理和生命科学等应用科学领域的许多现象中具有很大的优势,如非线性扩散、气体的燃烧和热交换、布朗运动等问题[4-5]. 此外,诸多学者都独立地探讨了各类分数阶微分方程初值问题[6-9].
本文主要讨论一类Caputo型分数阶微分方程边值问题:
(1)
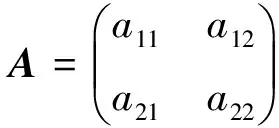
1 预备知识
首先,我们来介绍几个基本概念和一些Caputo分数阶导数的性质以及相关引理.
定义1[1]设Ω=[a,b]是R中的有限区间,∀α∈R+,则连续函数f(x)的α阶Riemann-Liouville分数阶积分定义为
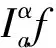

定义2[1]设Ω=[a,b]是R中的有限区间,∀α≥0,且n=[α]+1,则α阶Riemann-Liouville分数阶导数定义为
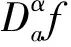
当α∉N时,n=[α]+1;当α∈N时,n=α.
定义3[1]设Ω=[a,b]是R中的有限区间,∀α∈R+,则连续函数f(x)的α阶Caputo分数阶导数定义为
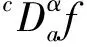
当α∉N时,n=[α]+1;当α∈N时,n=α.
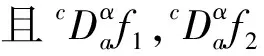
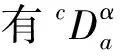
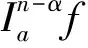
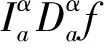
2 主要结果
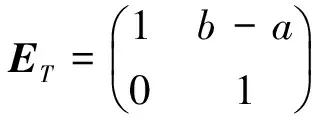
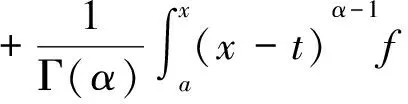
(2)
的解,即式(1)与(2)等价.其中λ1,λ2由线性方程
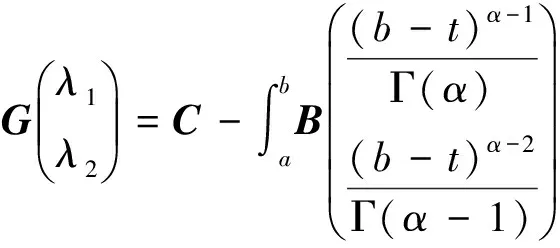
决定.
证明 首先证明必要性.由定义2和3可知
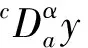
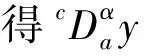
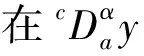
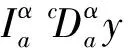
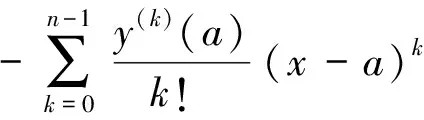
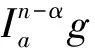
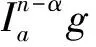
因为1<α<2,n=[α]+1=2,于是有
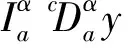
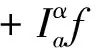
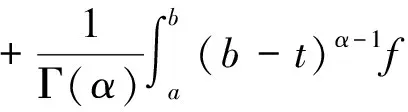
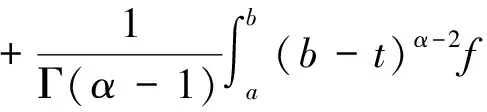
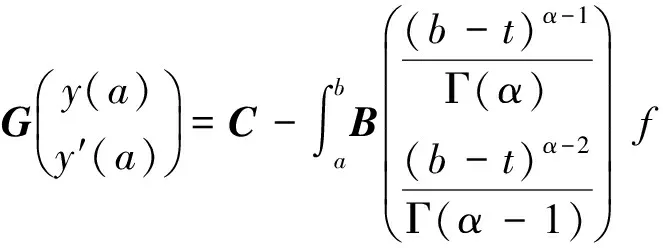
由此可知y∈C[a,b]是Fredholm积分方程(2)的解.
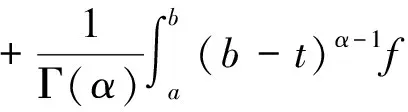
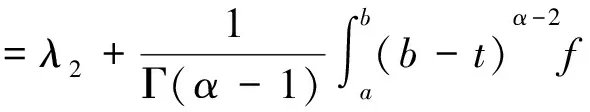
于是可以得到
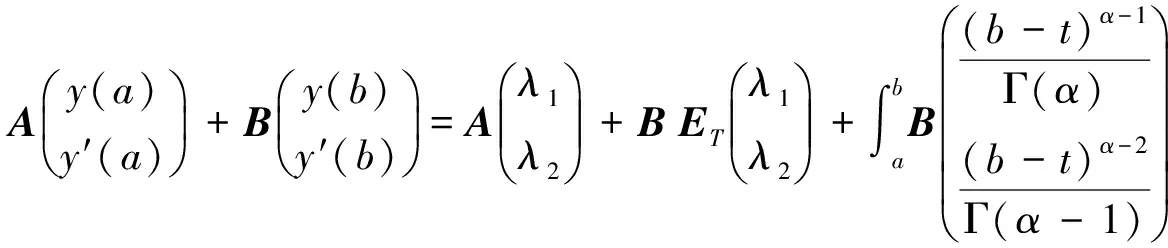
因此,y∈C[a,b]是Caputo型分数阶微分方程边值问题(1)的解.
定理2 在定理1的假设条件下,若f:[a,b]×R→R一致有界,则Caputo型分数阶微分方程边值问题(1)至少有一个解y∈C[a,b].
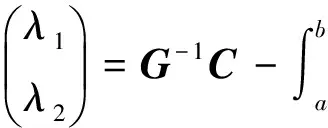
令U={y∈C[a,b]:‖y‖≤R},其中:
显然U是C[a,b]中的有界闭凸子集.
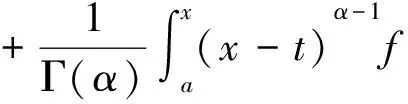
第一步:算子F是U→U的.
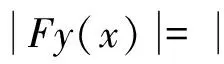
又由算子F的定义以及f的连续性知Fy∈C[a,b],则F:U→U.
第二步:算子F是连续的. 事实上,设{yn}∈U,且存在y∈U,使得yn→y(n→∞),则对任意的x∈[a,b],有
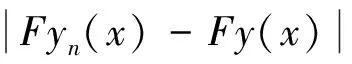
因为yn→y(n→∞),所以由f的连续性知‖f(t,yn(t))-f(t,y(t))‖→0(n→∞),故由‖Fyn(x)-Fy(x)‖→0(n→∞),由此说明算子F是连续的.
第三步:F(U)是一致有界的. 由第一步的证明以及U的定义,显然F(U)是一致有界的.
第四步:F(U)是等度连续的.任意的x1,x2∈[a,b],不妨设x1 由Ascoli-Arzela定理知F(U)是相对紧集,因此F:U→U全连续.根据Schauder不动点定理知F在U中至少有一个不动点. 综上,我们就证明了Caputo型分数阶微分方程边值问题(1)至少有一个解y∈C[a,b]. 则Caputo型分数阶微分方程边值问题(1)有唯一的解y∈C[a,b]. 证明 在C[a,b]上定义算子F:C[a,b]→C[a,b], 则在假设条件下算子F成为压缩算子,根据Banach不动点定理,Caputo型分数阶微分方程边值问题(1)有唯一的解y∈C[a,b]. 注:以上讨论了1<α<2时,Caputo型分数阶微分方程边值问题(1)的解的存在唯一性问题,事实上,当n-1<α 我们考虑如下Caputo型分数阶微分方程边值问题: 通过简单的计算,我们可以得到 [1] KILBAS A A, SRIVASTAVA H M,TRUJILLO J J. Theory and applications of fractional differential equations[M]. Amsterdam: Elsevier, 2006. [2] KENNETH S M, BERTRAM R. An introduction to the fractional calculus and fractional differential equations[M].New York: Wiley, 1993. [3] RAY S S.Fractional calculus with applications for nuclear reactor dynamics[M].Boca Raton:CRC Press,2015. [4] SABATIER J,SABATIER J, ALLGEMEIN H. Advances in fractional calculus[M]. Beijing:Beijing World Publishing Corporation,2014. [5] PODLUBNY I. Fractional differential equations[M].London: Academic Press, 1999. [6] ZHOU Y. Basic theory of fractional differential equations[M]. London:World Scientific, 2014. [7] JOHNNY H, RODICA L. Boundary value problems for systems of differential,difference and fractional equations[M]. New York:Elsevier,2016. [8] 刘东利,杨军,崔更新. 高阶分数阶微分方程边值问题正解的存在性[J]. 郑州大学学报(理学版),2014,46(1):16-20. [9] 梁秋燕. Banach空间分数阶微分方程边值问题解的存在性[J]. 郑州大学学报(理学版),2013,45(3):37-41. (责任编辑:王海科) Existence and Uniqueness of Solutions of Boundary Value Problem for a Caputo-type Fractional Differential Equation YANG Shuai1, ZHANG Shuqin2 (1.SchoolofMechanics&CivilEngineering,ChinaUniversityofMining&Technology,Beijing100083,China; 2.CollegeofScience,ChinaUniversityofMining&Technology,Beijing100083,China) The existence and uniquness of solutions of boundary value problem for a Caputo-type fractional differential equation were investigated. By transforming the boundary value problem into an equivalent Fredholm integral equation, and employing fixed point theorem in a Banach space, the existence and uniqueness of the solutions of the integral equation was proved. Caputo-type fractional differential equation; boundary value problem; Fredholm integral equation; fixed point 2016-10-21 国家自然科学基金项目(11371364). 杨帅(1990—),男,陕西榆林人,博士,主要从事应用数学与力学研究,Email:haotianwuji2@sina.com. O175.14 A 1671-6841(2017)02-0001-06 10.13705/j.issn.1671-6841.2016287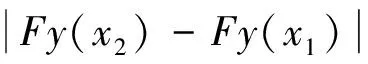
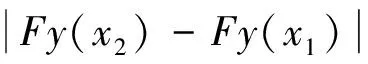
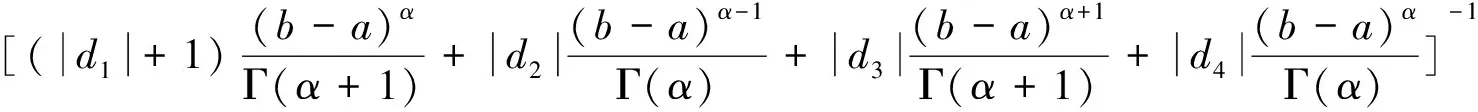
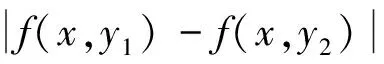
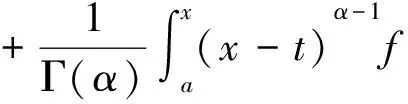
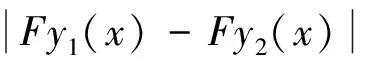
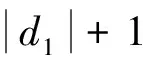
3 例子