基于离散粒子群算法的测试用例优先排序

张卫祥，齐玉华，李德治

(1.北京跟踪与通信技术研究所，北京 100094; 2.中国宇航学会 飞行器测控专委会，北京 100094)

(*通信作者电子邮箱vxiang@126.com)

基于离散粒子群算法的测试用例优先排序

张卫祥1,2*，齐玉华1,2，李德治1,2

(1.北京跟踪与通信技术研究所，北京 100094; 2.中国宇航学会 飞行器测控专委会，北京 100094)

(*通信作者电子邮箱vxiang@126.com)

测试用例优先排序技术能够有效提高回归测试效率，是软件测试的热点研究课题之一。针对基于需求的测试用例优先排序方法可操作性差的问题，提出了一种改进的基于测试点覆盖和离散粒子群优化算法的求解方法(TCP-DPSO)。首先，把影响排序的各种因素分为测试收益型因素和测试成本型因素两大类，通过加权平均的方式进行归一化，得到基于需求的通用测试平均收益率评价指标；然后，利用交换子和基本交换序列定义粒子的位置和速度，借鉴遗传算法(GA)变异策略引入变异算子，采用时变惯性权重调整粒子的探索能力和开发能力，促进可持续进化和逼近优化目标。实验结果表明，TCP-DPSO在最优解质量上与遗传算法相当，大幅优于随机测试，在最优解成功率和平均求解时间上优于遗传算法，具有更好的算法稳定性。

软件测试；测试用例优先排序；离散粒子群优化；评价指标；黑盒测试

0 引言

在软件的开发、维护过程中，由于修复软件缺陷、改进软件功能、增强软件性能或者重构部分代码等原因，经常需要对软件进行更动。近年来，随着增量式或迭代式软件开发方式的流行，软件更动得愈加频繁。回归测试可有效验证软件更动以及更动影响到的软件原有功能或模块的正确性，是保证软件质量的不可或缺的技术手段。但有数据表明，回归测试费用一般占软件维护预算的50%以上[1]。如何开展自动和高效的回归测试，已成为软件测试甚至软件工程领域的一个重要研究课题。

在回归测试中，测试用例的维护策略是一个核心问题[2]。一种简单的维护策略是重新执行全部已有的测试用例，但经常由于存在项目预算紧张、工程进度不允许、部分测试用例已失效、已有测试用例不能覆盖新增测试需求等诸多原因，导致重新执行全部用例是不可行的。为此，学术界和工业界对测试用例维护进行研究，提出了包括失效测试用例的识别和修复、测试用例选择、测试用例优先排序(Test Case Prioritization, TCP)、测试用例集缩减和测试用例集扩充等[3-4]在内的一系列典型技术。

TCP技术按照给定的排序准则对测试用例进行排序，通过优化测试用例的执行次序来达到提高软件测试效率的目的，一直是回归测试的研究热点之一[5]。Wong等[6]早在1997年进行了相关研究，结合测试用例历史覆盖信息和代码修改信息识别出冗余测试用例，对非冗余测试用例根据覆盖能力进行排序。Elbaum等[7]在2000年给出了TCP问题的一般性描述。Rothermel等[8]指出，除最大化测试用例集的早期缺陷检测速率外，还可以以代码覆盖率、高风险缺陷的检测率和系统可靠性等其他指标作为测试用例排序目标。陈翔等[5]把TCP技术分为基于代码的、基于模型的和基于需求的TCP等3类，目前基于代码的TCP技术研究较为充分，从贪婪法、机器学习法、融合专家知识法等不同角度已有不少的研究成果，相对而言基于需求的TCP技术的研究成果还不多见。

粒子群优化(Particle Swarm Optimization, PSO)算法是在1995年由Kennedy等[9]首先提出的。在PSO中，用一组多维向量表示不同粒子，根据个体最优解和群体最优解不断修正粒子的飞行方向和速度。由于相对简单、易于实现、参数少和不需要梯度信息等特点，PSO在连续优化问题和离散优化问题中都可取得良好效果，已成为智能优化领域近年来的一个研究热点。

在离散粒子群优化(Discrete PSO, DPSO)算法研究方面，Kennedy等[10]提出了一种针对0-1规划问题的二进制粒子群优化算法，每个粒子用一个二进制变量来表示，粒子的速度表示为二进制变量的翻转概率，通过变量翻转来实现粒子在空间中的移动。Hu等[11]给出了一种求解置换排列问题的方法，用置换排列表示粒子，用粒子的相似度来定义速度并决定粒子位置变化的概率。Clerc[12]给出一种求解TSP问题的方法，粒子位置用所有城市的一个排列来表示，所有城市的全部排列就构成了粒子的搜索空间。DPSO在电力系统、超大规模集成电路设计、无线传感器网络以及数据挖掘等领域中也有不少的应用研究[13]。

由于TCP问题本质上是寻找最优测试用例排列次序的离散优化问题，因此使用DPSO进行求解是可行的，但目前的研究还很少见，苏贝贝[14]提出了一种基于改进代码块覆盖的粒子群算法，用于结构测试中的TCP问题，而功能测试中的应用研究还未见到相关成果。

本文提出了一种求解TCP问题的DPSO(DPSO for TCP, TCP-DPSO)方法，主要思路是：

1)重新定义粒子的位置和速度，引入交换子和基本交换序列的概念，把粒子位置表示为所有测试用例的一个排列，把粒子速度定义为一个粒子位置变换为另一个粒子位置的基本交换序列。

2)提出基于需求的测试平均收益率评价指标，作为评估粒子位置优劣的适应度函数。

3)借鉴遗传算法(Genetic Algorithm, GA)中的变异策略，引入变异算子，促使群体可持续进化。

4)采用时变惯性权重，调整粒子的探索能力和开发能力。

实验验证及与已有成果的比较分析表明，TCP-DPSO能够有效求解TCP问题，且效果优于遗传算法和随机测试。

1 测试用例优先排序问题描述

1.1 基于需求的TCP问题

Elbaum等[7]对TCP问题给出的一般性描述为：给定测试用例集T、T的全排列集PT、排序目标函数f:PT→R，求解T′∈PT，使得对∀T″∈PT(T″≠T′)，有f(T′)≥f(T″)。

由一般性描述可知，函数f的每个输入是全部测试用例的一个特定执行次序，其输出值越大说明则排序效果越好。

按照TCP问题排序依据的不同，陈翔等[5]把TCP技术分为基于代码的、基于模型的和基于需求的TCP技术等3类。目前的研究主要集中在基于代码的TCP技术。

基于需求的TCP技术的研究成果还比较少。Srikanth等[15]考虑需求变更的可能性、客户定义的需求优先级、需求的实现复杂度和需求的缺陷倾向性等影响因素，提出了系统测试阶段的PORT排序方法。屈波等[16]基于测试用例的设计信息，提出了一组基于需求的测试用例优先级动态调整算法。Zhang等[17]提出了考虑测试需求优先级和测试用例执行开销的基于Total策略和Additional策略的TCP技术。Krishnamoorthi等[18]基于软件需求规约，考虑了包括需求优先级、需求变动信息、需求完整性、需求实现复杂度、需求可追踪性和缺陷影响程度等更多的影响因素，对测试用例进行排序。

综合考虑影响测试用例排序的各种因素，总体上可以分为两大类：测试成本型因素(Cost-Keys)，主要表现于测试用例执行花销等；测试收益型因素(Win-Keys)，主要表现于测试需求的重要程度和缺陷的潜在危害等。Cost-Keys和Win-Keys包含了上面提到的各种影响因素。有的影响因素所起的作用和测试用例次序是正相关的，有的是负相关的，有的影响大，有的影响小，但都可以通过加权平均的方式进行归一化。

不失一般性，令Cost-Keys因素全集为C={c1,c2,…,cn}，Win-Keys因素全集为W={w1,w2,…,wm}，对任一测试用例ti∈T，有：

(1)

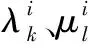
下节将利用Wi、Ci给出基于需求的TCP技术的一种通用量化指标——测试平均收益率评价指标。

1.2 评价指标APWC

与随机测试相比，TCP技术的一个显著优点是能够更快地检查出错误。基于此，Elbaum等[19]给出APFD(AveragePercentageofFaultDetection)评价指标,采用测试用例使用个数和检测错误个数之间的关系来量化测试用例序列的优劣。当给定测试用例的执行次序时，可用APFD指标计算测试用例执行过程中检测到缺陷的平均累计比例，但需要事先知晓测试用例的缺陷检测信息。一般地，缺陷检测信息在测试用例全部执行前是不可能知道的，所以APFD存在着明显不足。

Li等[20]随后提出APBC(AveragePercentageofBlockCoverage)、APDC(AveragePercentageofDecisionCoverage)和APSC(AveragePercentageofStatementCoverage)等系列指标，分别量化测试用例序列对程序块、分支和语句的覆盖速率。由于在测试用例执行之前可以通过覆盖率分析工具得到覆盖率信息，故可在测试用例全部执行之前使用APBC、APDC和APSC等指标，但是这些指标显然更适合于基于代码的结构测试。

在基于需求的功能测试中，测试人员以软件规格说明为依据，进行测试用例的设计。一般流程是：首先将软件需求转化为测试需求；其次把测试需求细化分解为测试点；然后针对测试点进行测试用例设计；最后形成测试用例集合。张卫祥等[21]提出基于测试点覆盖的评价指标APTC(Average Percentage of Test-Point Coverage)。对于测试用例集Φ={T1,T2,…,Tn}，APTC的计算公式[21]定义为：

(2)

其中，TTi表示首个可覆盖到第i个测试点的测试用例在该用例序列中所处的次序，m为测试点个数，n为测试用例个数。APTC的取值范围为0～100%，取值越高说明对测试点覆盖的速率越快。

在这里，考虑到各因素对测试用例排序结果的影响，根据上节的分析，利用式(1)中的综合收益和综合成本对APTC进行改进。把评估目标调整为单位综合成本取得的综合收益，提出测试平均收益率评价指标APWC(Average Percentage of Win-Cost Coverage)。

APWC公式化表示为：

考虑如表 1所示的实例，共有10个测试点1～10和5个测试用例A～E，对于两个不同的测试用例序列A-B-C-D-E和E-D-C-B-A，计算可得APTC取值分别为50%、64%，故执行次序2的效果优于执行次序1。图 1中折线下方阴影面积占整个面积的比例即为各执行次序的APTC值。

表1 测试用例与测试点的对应关系的一个实例

现假设，测试用例B的综合成本CB是其他测试用例的2倍，但其综合收益WB高于其他测试用例，它所覆盖的测试点(即测试点1，5，6，7)的重要程度是其他测试点的2倍。即，在假设单位成本和单位重要程度均为1的情况下，测试用例B的综合成本为2，测试点1，5，6，7重要程度值为2。根据公式可计算测试用例序列A-B-C-D-E和E-D-C-B-A的APTW的取值分别为56%和68%，如图2所示。

可见，在不同测试用例的成本与收益差别较大时，APWC能够更为准确地反映测试用例优先执行序列的价值。

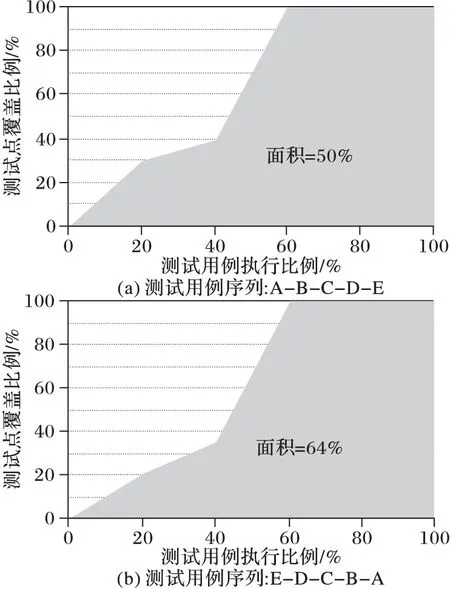
图1 不同测试用例序列对应的APTC值

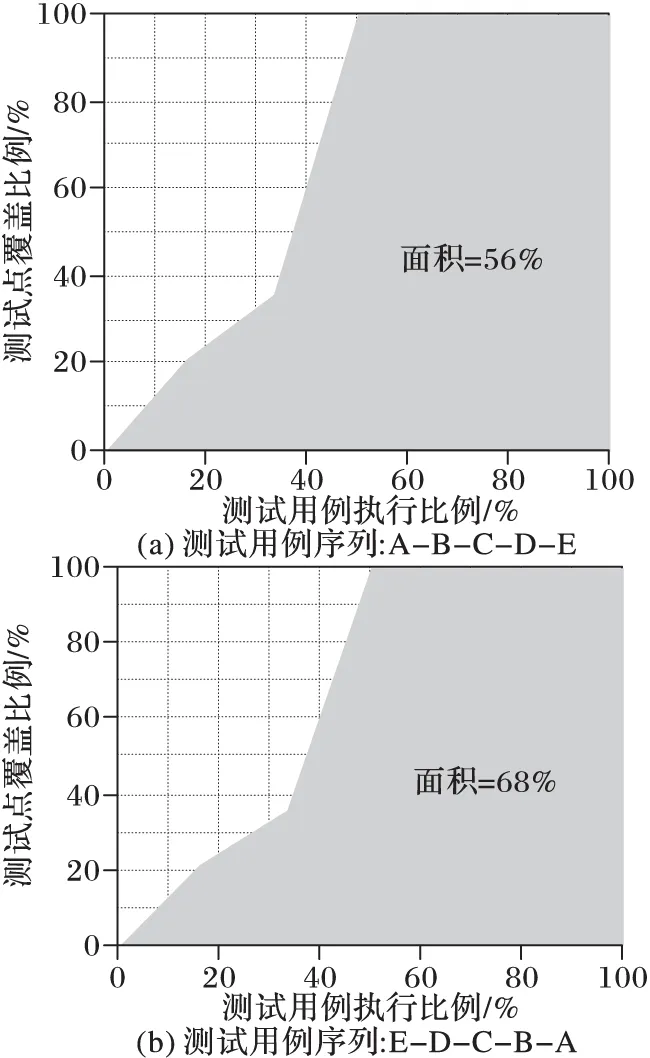
图2 不同测试用例序列对应的APWC值

2 基于离散粒子群优化的求解方法

本章给出求解TCP问题的离散粒子群优化(DPSO for TCP， TCP-DPSO)算法。首先介绍标准粒子群优化算法，随后给出TCP-DPSO算法的实现原理和基本流程。

2.1 标准粒子群优化算法

粒子群优化算法的基本思想是：由m个粒子组成的群体在D维搜索空间中以一定的速度各自飞行以寻找最佳位置(最优解)，每个粒子在搜索时，受到自身历史最好点和群体内其他粒子历史最好点的影响，不断进行自身位置优化。

假设第i个粒子的位置表示为xi=(xi1,xi2,…,xiD)，速度为vi=(vi1,vi2,…,viD)，1≤i≤m。第i个粒子的历史最好点为pi=(pi1,pi2,…,piD)，群体内所有粒子的历史最好点为pg=(pg1,pg2,…,pgD)。

粒子的位置和速度根据式(4)～(5)进行变化：

(4)

(5)

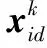
基于上述原理优化的粒子群算法被称为标准粒子群优化算法，最初用于解决连续优化问题，速度变量是连续的，但是许多实际应用问题，比如著名的旅行商问题(TravelingSalesmanProblem,TSP)，是离散的，其变量是有限的，因此需要研究离散版本的粒子群算法。最典型的两种离散策略是二进制编码和顺序编码。下节采用顺序编码策略，提出用于TCP问题的TCP-DPSO算法。

2.2 TCP-DPSO算法实现原理

2.2.1 粒子群编码

对于含有n个测试用例的测试用例集T={t1,t2,…,tn}和给定的排序目标f，TCP问题的实质是找到一个测试用例序列，使得排序目标f达到最优。

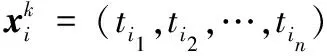
为了表示粒子速度，引入交换子和基本交换序的概念。

定义1 交换子。对于任一粒子位置，一个交换子s=s(p,q)的作用是交换其第p个和第q个元素的位置，从而形成一个新的粒子位置。

定义2 交换序列。称一个或多个交换子的有序队列为一个交换序列，记为S=(s1,s2,…,sl)。在交换序列中，各交换子的顺序是有意义的，因为一个交换序列作用于某粒子位置上，意味着此交换序列中的所有交换子依次作用于该粒子位置上。交换序列中包含的交换子的个数称为交换序列的长度。

例如，粒子位置x经S作用后变为x″，即x″=x+S=x+(s1,s2,…,sl)=[(x+s1)+s2]+…+sl。

定义3 基本交换序列。不同的交换序列作用在同一粒子位置上可能产生相同的效果，称具有相同作用效果的交换序列的集合为交换序列的等价集，称拥有最少交换子的交换序列为该等价集的基本交换序列。

可以看出，粒子速度就是从一个粒子位置变换为另一个粒子位置的交换序列。为了保证唯一性，令粒子速度取基本交换序列。

2.2.2 粒子位置与速度的迭代方程

为了给出粒子位置与粒子速度的迭代方程，需要定义减法算子(粒子位置与粒子位置相减)、加法算子(粒子位置与粒子速度相加)、乘法算子(粒子速度与实数相乘)、合并算子(粒子速度与粒子速度相加)。

定义4 减法算子-。两个粒子位置进行减法运算，其结果是一组交换子，准确地讲，是减数变成被减数所需的一个基本交换序列(粒子速度)。

例如，对粒子位置x1=(1,2,3,4,5)和x2=(3,1,5,2,4)，x2-x1=((1,3),(2,3),(3,5),(4,5))。

定义5 加法算子+。粒子位置与粒子速度相加，其结果是把粒子速度对应的交换序列作用于该粒子位置后形成的新粒子位置。加法算子满足交换律。

例如，对粒子位置x1=(1,2,3,4,5)和粒子速度v1=((1,3),(2,3),(3,5),(4,5))，其和x1+v1=v1+x1=(3,1,5,2,4)。

定义6 乘法算子×。粒子速度(长度为l的交换序列S)与实数α∈[0,1]的乘法运算，其结果是对S的交换子队列截断而形成的长度为α×l(取整)的新交换序列S′。

定义7 合并算子⊕。粒子速度的合并运算就是对它们对应的交换序列的合并操作，其结果是把后一个交换序列的交换子队列连接到前一个交换序列的交换子队列的队尾，形成一个更长的交换序列。合并运算满足分配律。

根据上述定义，对式(4)、(5)进行更新，给出TCP-DPSO算法粒子位置与速度的迭代方程：

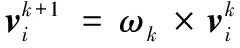
(6)

(7)

其中：ωk为惯性权重，将在下节介绍；α、β分别表示粒子自身极值和群体全局极值对粒子的影响程度，值越大说明影响程度越大。为了平衡粒子的自我总结和向群体中优秀个体学习的能力，进行如下设置：当迭代次数不大于最大迭代次数的一半时(k≤Kmax/2)，取α=Cmax,β=Cmin；否则，取α=Cmin,β=Cmax。一般地，可令Cmax=0.95,Cmin=0.35。

2.2.3 惯性权重设计

惯性权重是粒子群优化算法的重要参数，常见的设置方法有固定权重、时变权重、模糊权重等。固定权重方法赋予惯性权重一个0和1之间的常数值，有实验表明，群体规模越小需要的惯性权重越大，反之亦然。模糊权重方法使用模糊系统来动态调节惯性权重，例如Shi等[22]使用了具有9条规则、2个输入和1个输出的模糊系统。时变权重方法能使粒子群在初期具有较好的探索能力，而在后期具有较好的开发能力。

假设惯性权重的取值范围为[ωmin,ωmax]，最大迭代次数为Kmax，TCP-DPSO算法采用式(8)定义第k次迭代时的惯性权重：

ωk=ωmax-(ωmax-ωmin)×(k/Kmax)2

(8)

一般地，令ωmax=0.9，ωmin=0.4，Kmax根据实际问题确定。

2.2.4 变异策略设计

随着迭代的进行，由于排列的趋同性，在粒子到达局部最优位置附近时，不活跃粒子的速度将会越来越小，甚至停止运动。因此，在TCP-DPSO算法中引入变异策略，用随机产生的新粒子替换趋于停滞的粒子，以促进群体的可持续进化。

具体地，设置临界值SimilarDegree，在每次迭代后对粒子活跃度进行判断，当一个粒子与局域最优位置的排列相似度(测试用例个数)大于SimilarDegree时，随机生成新粒子替代该粒子。

2.2.5 适应度函数设计

以执行测试序列时单位综合成本取得的综合收益为评价目标，采用式(3)定义的测试平均收益率评价指标APWC作为适应度函数Fitness，也可采用其他评价指标。

需注意的是，APWC为一般性指标，可通过设置适当假设条件或选择特定参数使其进行简化，例如，假设所有测试用例的综合收益相同且综合成本相等，APWC就简化为文献[21]中的APTC。

2.3 TCP-DPSO算法基本流程

TCP-DPSO算法的基本步骤包括：

1)对粒子群进行随机初始化，给每个粒子赋予一个随机的初始位置和一个随机的交换序列。

2)使用适应度函数Fitness计算每个粒子的适应度值。

3)比较每个粒子的当前适应值和自身历史最优位置pi的适应值，如果当前值更优，则更新pi。

4)比较每个粒子的当前适应值和群体最优位置pg的适应值，如果当前值更优，则更新pg。

5)使用变异策略判断每个粒子的活跃度，并用随机产生的新粒子替换趋于停滞的粒子。

6)使用式(8)调整时变惯性权重ωk。

7)使用式(6)和式(7)更新粒子的速度和位置。

8)如果当前迭代次数k达到预设的最大迭代次数或者pg的适应值已足够好，算法结束；否则，k加1，返回第2)步。

3 实验验证

3.1 实验设置

实验采用三角形分类程序，并与文献[21](利用遗传算法和随机测试方法)进行结果比较。

三角形分类程序通过分析输入变量的取值及其相互关系，来判断它们将组成何种三角形。三角形分类程序共有7个测试点，如表 2所示，设计测试用例6个，测试用例与测试点的关系如表3所示。

由于粒子群算法和遗传算法都是启发式方法，不能保证在任何情况下都能得到最优解。为了检验算法的效果，从两个方面进行考虑：首先是求得的最优解的质量，其次是最优解的平均生成时间。

为了便于比较，分别采用APWC的两种简化变体APWC-1和APWC-2作为TCP-DPSO的适应度函数，其中，APWC-1的简化原则是令所有测试用例的综合收益相同且综合成本相等，即如果所有测试用例的综合收益相同且综合成本相等，APWC就简化为APWC-1，等价于文献[21]的APTC；APWC-2的简化原则是假设每个测试点的重要程度及每个测试用例的成本不等，以单位测试成本覆盖测试点的重要性程度值作为评价目标，APWC-2等价于文献[21]的APTC_C。

TCP-DPSO的主要参数配置如表4所示，其中Cmax=0.95，Cmin=0.35，ωmax=0.9，ωmin=0.4。

表2 三角形分类程序的测试点[21]

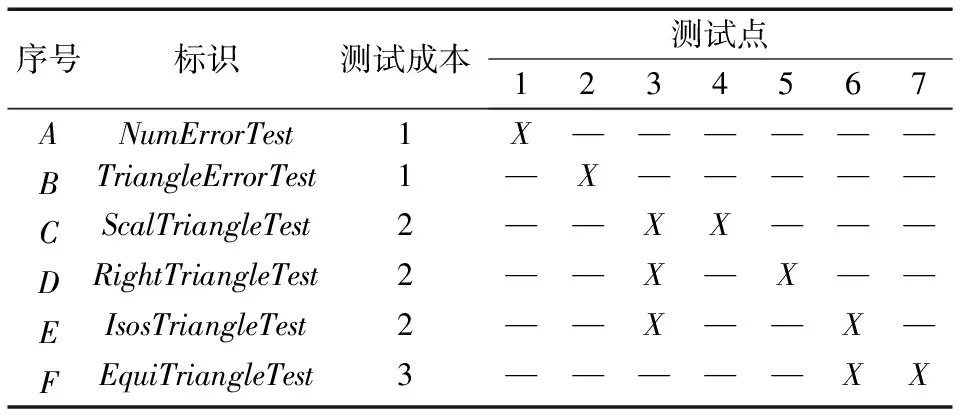
表3 三角形分类程序的测试点与测试用例的对应关系[21]

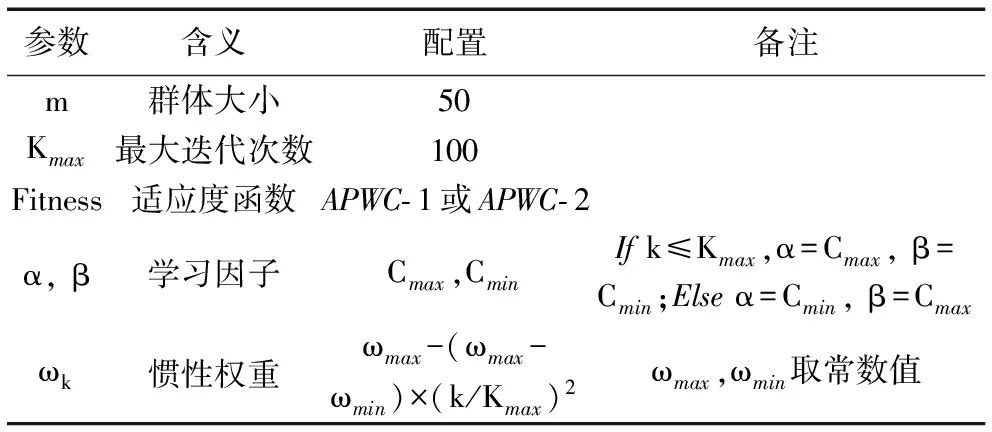
表4 TCP-DPSO的主要参数配置

3.2 结果分析

TCP-DPSO求得的最优序列及其与文献[21]的比较如表5所示。

TCP-DPSO与遗传算法(GA)[21]的最优序列的平均求解时间如表6所示。运行环境为：IntelCore2Duo1.40GHz，2.94GB内存、WindowsXP、Matlab。

由表5可见，在求解最优序列的效果方面，TCP-DPSO与遗传算法相当，大幅优于随机测试。由表6可以得到，在求解最优解即最优测试序列的成功率方面，TCP-DPSO略优于遗传算法；而在平均求解时间上，TCP-DPSO也比遗传算法要略优，说明TCP-DPSO算法的稳定性更好。

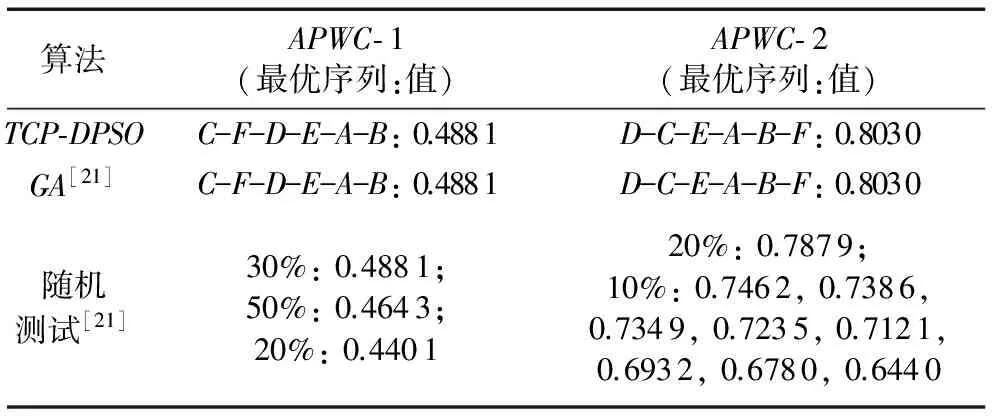
表5 不同方法最优序列比较

表6 不同方法最优序列平均求解时间比较

4 结语

测试用例优先排序问题的实质是找到一个测试用例序列，使得排序目标达到最优。粒子群优化算法能够有效减少测试用例排序过程中的盲目性，提高排序搜索的速度和效果，从而提高软件测试效率。

TCP-DPSO算法基于群体进化思想，通过个体间协作和相互竞争来寻找最优解，若粒子当前位置比所经历过的最优位置有更好的适应度值，将替换其经历的最优位置；粒子还能够从全局最优值中取得更新信息，使粒子不断地向群体经验认可好的方向飞行；另外引入变异机制，避免陷于局部最优，使得快速地达到或逼近优化目标。实验数据表明，TCP-DPSO算法效果优于遗传算法和随机测试。

利用智能优化技术求解测试用例优先排序、测试用例约简、测试自动化生成等软件测试中的热门问题，是一个可行的技术方向，具有很好的研究价值。下一步将就粒子群算法、遗传算法、蚁群算法、模拟退火等在软件测试中的应用作进一步的研究。

)

[1]AMMANNP,OFFUTTJ.IntroductiontoSoftwareTesting[M].Cambridge,UK:CambridgeUniversityPress, 2008: 9-10.

[2]ORSOA,ROTHERMELG.Softwaretesting:aresearchtravelogue(2000—2014) [C]//FOSE2014:ProceedingsoftheFutureofSoftwareEngineering.NewYork:ACM, 2014: 117-132.

[3]YOOS,HARMANM.Regressiontestingminimization,selectionandprioritization:asurvey[J].SoftwareTesting,Verification&Reliability, 2012, 22(2): 67-120.

[4]HARROLDM,ORSOA.Retestingsoftwareduringdevelopmentandmaintenance[C]//Proceedingsofthe2008FrontiersofSoftwareMaintenance.Piscataway,NJ:IEEE, 2008: 99-108.

[5] 陈翔,陈继红,鞠小林,等.回归测试中的测试用例优先排序技术述评[J].软件学报,2013,24(8):1695-1712.(CHENX,CHENJH,JUXL,etal.Surveyoftestcaseprioritizationtechniquesforregressiontesting[J].JournalofSoftware, 2013, 24(8): 1695-1712.)

[6]WONGW,HORGANJ,LONDONS,etal.Astudyofeffectiveregressiontestinginpractice[C]//Proceedingsofthe1997InternationalSymposiumonSoftwareReliabilityEngineering.Piscataway,NJ:IEEE, 1997: 264-274.

[7]ELBAUMS,MALISHEVSKYAG,ROTHERMELG.Prioritizingtestcasesforregressiontesting[C]//Proceedingsofthe2000InternationalSymposiumonSoftwareTestingandAnalysis.NewYork:ACM, 2000: 102-112.

[8]ROTHERMELG,UNTCHRH,CHUC,etal.Testcaseprioritization:anempiricalstudy[C]//Proceedingsofthe1999InternationalConferenceonSoftwareMaintenance.Piscataway,NJ:IEEE, 1999: 179-188.

[9]EBERHARTRC,KENNEDYJ.Anewoptimizerusingparticlesswarmtheory[C]//ProceedingsoftheSixthInternationalSymposiumonMicroMachineandHumanScience.Piscataway,NJ:IEEE, 1995: 39-43.

[10]KENNEDYJ,EBERHARTR.Adiscretebinaryversionoftheparticleswarmoptimization[C]//Proceedingsofthe1997IEEEInternationalConferenceonNeuralNetworks.Piscataway,NJ:IEEE, 1997: 4104-4108.

[11]HUXH,EBERHARTRC,SHIYH.Swarmintelligenceforpermutationoptimization:acasestudyofn-queens problem [C]// Proceedings of the 2003 IEEE Swarm Intelligence Symposium.Piscataway, NJ: IEEE, 2003: 243-246.

[12] CLERC M.Discrete particle swarm optimization-illustrated by the traveling salesman problem [EB/OL].[2016-03-20].http://clerc.maurice.free.fr/pso/pso_tsp/Discrete_PSO_TSP.htm.

[13] 徐华,张庭.改进离散粒子群算法求解柔性流水车间调度问题[J].计算机应用,2015,35(5):1342-1347.(XU H, ZHANG T.Improved discrete particle swarm algorithm for solving flexible flow shop scheduling problem [J].Journal of Computer Applications, 2015, 35(5): 1342-1347.)

[14] 苏贝贝.基于粒子群算法的软件测试用例优先排序方法研究[D].重庆:重庆大学,2012:13-41.(SU B B.Study on test case prioritization based on particle swarm optimization [D].Chongqing: Chongqing University, 2012: 13-41.)

[15] SRIKANTH H, WILLIAMS L, OSBORNE J.System test case prioritization of new and regression test cases [C]// Proceedings of the 2005 International Symposium on Empirical Software Engineering.Piscataway, NJ: IEEE, 2005: 64-73.

[16] 屈波,聂长海,徐宝文.基于测试用例设计信息的回归测试优先级算法[J].计算机学报,2008,31(3):431-439.(QU B, NIE C H, XU B W.Test case prioritization based on test suite design information [J].Chinese Journal of Computers, 2008, 31(3): 431-439.)

[17] ZHANG X F, NIE C H, XU B W, et al.Test case prioritization based on varying testing requirement priorities and test case costs [C]// Proceedings of the 2007 International Conference on Quality Software.Piscataway, NJ: IEEE, 2007: 15-24.

[18] KRISHNAMOORTHI R, SAHAAYA ARUL MARY S A.Factor oriented requirement coverage based system test case prioritization of new and regression test cases [J].Information and Software Technology, 2009, 51(4): 799-808.

[19] ELBAUM S, MALISHEVSKY A, ROTHERMEL G.Prioritizing test cases for regression testing [C]// Proceedings of the 2000 International Symposium on Software Testing and Analysis.New York: ACM, 2000: 102-112.

[20] LI Z, HARMAN M, HIERONS R M.Search algorithms for regression test case prioritization [J].IEEE Transactions on Software Engineering, 2007, 33(4): 225-237.

[21] 张卫祥,魏波,杜会森.一种基于遗传算法的测试用例优先排序方法[J].小型微型计算机系统,2015,36(9):1998-2002.(ZHANG W X, WEI B, DU H S.Test case prioritization method based on genetic algorithm [J].Journal of Chinese Computer Systems, 2015, 36(9): 1998-2002.)

[22] SHI Y, EBERHART R.Fuzzy adaptive particle swarm optimizer [C]// Proceedings of the 2001 IEEE International Congress on Evolutionary Computation.Piscataway, NJ: IEEE, 2001: 101-106.

This work is supported by the National Natural Science Foundation of China (61502015).

ZHANG Weixiang, born in 1979, M.S., engineer.His research interests include software testing, intelligent testing.

QI Yuhua, born in 1985, Ph.D., assistant researcher.His research interests include software testing, defect analysis and repair.

LI Dezhi, born in 1963, M.S., senior engineer.His research interests include software testing, software engineerization.

Test case prioritization based on discrete particle swarm optimization algorithm

ZHANG Weixiang1,2*, QI Yuhua1,2, LI Dezhi1,2

(1.BeijingInstituteofTrackingandTelecommunicationsTechnology,Beijing100094,China;2.CommitteeofSpacecraftTT&CTechnology,ChineseSocietyofAstronautics,Beijing100094,China)

With the ability to improve regression testing efficiency, test case prioritization has become a hot topic in software testing research.Since test case prioritization based on requirement is usually inefficient, a test case prioritization method based on discrete particle swarm optimization and test-point coverage, called Discrete Particle Swarm Optimization for Test Case Prioritization (TCP-DPSO) was proposed.Firstly, the various factors affecting prioritization were divided into two categories: Cost-Keys and Win-Keys, and then general test average yield index by normalizing was obtained.Then, particle’s position and velocity were defined by use of switcher and basic switching sequence, the mutation operator was introduced by referencing mutation strategy of Genetic Algorithm (GA), and the exploration and development capabilities were adjusted by adopting variable inertia weight, which could promote sustainable evolution and approach optimization goals.The experimental results show that TCP-DPSO is similar to GA and dramatically better than random testing on optimal solution quality and it is superior to GA on success rate and average computing time, which indicates its better algorithm stability.

software testing; test case prioritization; Discrete Particle Swarm Optimization (DPSO); evaluation index; functional testing

2016-08-24;

2016-09-04。 基金项目:国家自然科学基金资助项目(61502015)。

张卫祥(1979—)，男，山东济宁人，工程师，硕士，主要研究方向：软件评测、智能化测试； 齐玉华(1985—)，男，河南睢县人，助理研究员，博士，主要研究方向：软件评测、缺陷分析与修复； 李德治(1963—)，男，河南偃师人，高级工程师，硕士，主要研究方向：软件评测、软件工程化。

1001-9081(2017)01-0108-06

10.11772/j.issn.1001-9081.2017.01.0108

TP311.5; TP181

A