MapReduce并行加速数据流多模式相似性搜索
2017-04-17付晨,钟诚,叶波
付 晨,钟 诚,叶 波
(1.广西大学 计算机与电子信息学院,南宁 530004; 2.广西科技信息网络中心,南宁 530012)
(*通信作者电子邮箱chzhong@gxu.edu.cn)
MapReduce并行加速数据流多模式相似性搜索
付 晨1,钟 诚1*,叶 波2
(1.广西大学 计算机与电子信息学院,南宁 530004; 2.广西科技信息网络中心,南宁 530012)
(*通信作者电子邮箱chzhong@gxu.edu.cn)
设计时间序列数据在Hadoop分布式文件系统(HDFS)中的有效存储方式,利用分布式缓存工具Distributed Cache将各子序列分发到Hadoop集群的计算节点上,将动态时间弯曲距离矩阵划分成多个子矩阵,采取并行迭代计算每条反对角线上子矩阵的方法,基于MapReduce编程模型,实现高效并行计算时间序列动态弯曲距离,通过改进剪裁冗余计算方法,设计实现一种数据流多模式相似性搜索并行算法。中国雪深长时间序列数据集的实验结果表明,当每条时间序列的长度达到5 000以上时,并行计算动态弯曲距离所需时间少于串行计算所需时间,当每条时间序列的长度达到9 000以上时,参与计算的集群节点越多,并行计算所需时间越少;当模式长度达到4 000、参与计算的集群节点数达5个以上时,从数据流中并行搜索出与模式匹配的相似子序列所需时间约为串行搜索所需时间的20%。
时间序列;数据流;动态时间弯曲距离;模式搜索;Hadoop
0 引言
时间序列数据流相似性搜索在网络点击流分析、金融分析、气象监测、语音识别等诸多领域具有广泛的应用[1]。大数据环境下长时间序列数据流多模式相似性搜索十分耗时。因此,在分布式并行计算Hadoop平台上,研究设计实现高效的数据流多模式相似性搜索并行算法具有重要应用价值。
欧氏距离及其扩展的相似性度量方法针对时间序列在时间轴上拉伸、收缩、平移等变形的健壮性不强[2]。动态时间弯曲(Dynamic Time Warping, DTW)距离[3]能够度量不同步不等长的时间序列,使它们通过一定的变形进行比较,适合于时间序列相似性比较。文献[4]利用MPI(Message Passing Interface)和Open MP机制,采取均匀划分数据分配方法,设计机群计算时间序列动态弯曲距离的并行算法,获得了较好的加速。文献[5]针对无线传感器网络环境下不确定异常时间序列检测效率低下的问题,对不确定时间序列进行压缩变换,以减少不确定数据量,利用MapReduce架构实现基于期望距离的不确定时间序列动态弯曲距离算法并行化,同时提出了基于显著特征匹配的局部约束算法,对弯曲路径进行局部限制,提高了检测效率。文献[6]提出一种判断累加距离是否超出阈值的推算方法,以减少一些不必要的冗余计算。文献[7]利用值域划分柱图,将时间序列映射到k维空间,构造新的距离函数,获得动态时间弯曲距离的新的上、下界,从而缩小原始候选集,使算法仅需在小规模候选集上计算DTW距离,降低了计算复杂度。时间序列动态弯曲距离的一个重要应用是被用来搜索数据流中的相似模式。通过保存时间序列累计距离和候选序列的起始点,采取计算时间子序列匹配矩阵的方法,文献[8]的SPRING算法解决了针对数据流连续、实时、无限制等特性的时间序列的子序列匹配问题,但该算法存在冗余计算。文献[9]构造一个计分函数来降低动态时间弯曲距离的计算量,然后利用得到的时间弯曲距离来搜索发现数据流中公共的局部相似模式。
本文基于Hadoop平台,通过设计时间序列数据在HDFS中的有效存储方式和改进剪裁减少冗余计算方法,采取MapReduce并行迭代计算每条反对角线上动态时间弯曲距离子矩阵的方法,设计实现高效的数据流多模式相似性搜索并行算法,在获得较好匹配效果的同时,大大缩短计算时间。
1 MapReduce并行计算动态时间弯曲距离
1.1 递推计算动态时间弯曲距离
采用递推方法计算时间序列X={x1,x2,…,xm}和Y={y1,y2,…,yn}之间的动态弯曲距离矩阵D(X,Y)[9]:
(1)
其中c=min{d(i,j-1),d(i-1,j),d(i-1,j-1)},i=1,2,…,m,j=1,2,…,n。从动态时间弯曲距离矩阵中可以寻找出弯曲路径DTW(X,Y)={w1,w2,…,wk},从而得到X和Y之间的匹配关系。
1.2 数据存储与算法设计
1.2.1 算法设计
采用MapReduce编程模型可有效处理大规模科学计算问题[10]。为了在Hadoop平台上实现并行计算动态时间弯曲距离矩阵,将序列X划分为长度分别为「m/p⎤的p个子序列X0,X1,…,Xp-1,并将序列Y划分为长度分别为「n/q⎤的q个子序列Y0,Y1,…,Yq-1。利用Hadoop分布式缓存工具Distributed Cache将各子序列分发到Hadoop集群计算节点上,于是构造p×q个子矩阵D(f,g),f=1,2,…,p,g=1,2,…,q,每个子矩阵规模为「m/p⎤×「n/q⎤,这些子矩阵D(f,g)可以并行计算[11]。
算法1描述了Hadoop平台上并行计算动态时间弯曲距离(ParallelComputingDistancesofTimeWinding,PCDTW)算法。
算法1PCDTW算法。
输入:时间序列X和Y。 输出:动态时间弯曲距离矩阵D。Begin1) 计算子矩阵D(1,1),将其最后一行和最后一列存入HDFS中; 2) 读取HDFS中D(1,1)最后一行,存入D(2,1)的第0行,用于D(2,1)的计算;读取HDFS中D(1,1)最后一列,存入D(1,2)的第0列,用于D(1,2)的计算;将D(2,1)的最后一行与D(1,2)的最后一列存储到HDFS中; 3) 获取子矩阵D(2,1)的最后一行,存入D(3,1)的第0行;获取D(1,2)的最后一行及D(2,1)的最后一列,分别存入D(2,2)的第0行和第0列;获取D(1,2)的最后一列,存入D(1,3)的第0列;并行计算D(3,1)、D(2,2)和D(1,3); 4) 依此类推,获取子矩阵D(f-1,g)的最后一行及D(f,g-1)的最后一列,存入D(f,g)的第0行和第0列,计算D(f,g),将D(f,g)的最后一行传送给D(f+1,g)计算,将D(f,g)的最后一列传送给D(f,g+1)计算;并行计算每条反对角线上的子矩阵,每次Map/Reduce过程完成计算一条反对角线上的子矩阵; 5) 若距离累加超过事先设定的阈值,则算法结束;否则迭代k=p+q-1次,并行计算D(f,g);End
1.2.2 动态时间弯曲距离矩阵数据存储设计
HDFS文件中每一行存储动态时间弯曲距离子矩阵中每个元素的信息,子矩阵信息用坐标(子矩阵分块行号,子矩阵分块列号)表示,元素信息包括(行号,列号#元素值)。HDFS中每一行的存储格式为〈(子矩阵分块行号,子矩阵分块列号)(元素行号,元素列号#元素值)〉,即以〈(f,g)(i,j#d[i][j])〉的形式存储,f和g代表子矩阵在动态时间弯曲距离矩阵分块中的行、列号,i和j为子矩阵元素在子矩阵中的行、列号,d[i][j]代表元素值。
1.2.3Map过程的设计
并行计算Map阶段的主要工作:从HDFS文件中逐行读取动态时间弯曲距离矩阵数据〈(f,g)(i,j#d[i][j])〉;筛选出本次计算的子矩阵分块坐标(f,g),获取子矩阵的第0行元素和第0列元素。
如果上一轮迭代计算有相关子矩阵传递最后一行记录数据,那么本次计算的子矩阵用第0行接收。如果上一轮迭代计算有相关子矩阵传递最后一列记录数据,那么本次计算的子矩阵用第0列接收。
算法2 并行计算DTW距离的Map函数。
输入:〈key1,value1〉为〈行号,HDFS中每一行记录〉。 输出:中间结果〈key2,value2〉。Begin1) 逐行读取HDFS文件,获取子矩阵中每个元素信息〈(f,g)(i,j#d[i][j])〉: ①key1←行号; ②value1←〈(f,g)(i,j#d[i][j])〉。 2) 筛选出本轮迭代计算的子矩阵分块坐标(f,g),记录其第0行和第0列信息; 3) 将中间结果〈key2,value2〉写入本地节点的中间文件: ①key2←(f,g);value2←(0,j#d[0][j]); 将中间结果〈key2,value2〉以“〈(子矩阵分块行号,子矩阵分块列号)(第0行,元素列号#元素值)〉”的形式(即〈(f,g)(0,j#d[0][j])〉)写入本地中间文件; ②key2←(f,g);value2←(i,0#d[i][0]); 将中间结果〈key2,value2〉以“〈(子矩阵分块行号,子矩阵分块列号)(元素行号,第0列#元素值)〉”的形式(即〈(f,g)(i,0#d[i][0])〉)写入中间文件;End
算法2中步骤3)的中间结果key2值为本次计算的子矩阵坐标(f,g),相应的value2值为本次计算子矩阵第0行每个元素信息(0,j#d[0][j])或者第0列元素的信息(i,0#d[i][0])。通过算法2可筛选本次计算的子矩阵分块坐标(f,g),获取本次计算的子矩阵的第0行元素和第0列元素,并将其记录到中间文件。
1.2.4Reduce函数的设计
并行计算Reduce阶段的任务:根据输入的键值对〈key2,list〈value2〉〉,接收相同key2值对应的list〈value2〉得到本次计算子矩阵第0行元素集合和第0列元素集合。提取分布式缓存中本次参与计算子序列Xf和Yg。记录本轮迭代计算的反对角线上的各个DTW距离子矩阵,同时将子矩阵最后一行和最后一列写到HDFS结果文件中,以传递给下一轮迭代计算时Map函数使用。
算法3 并行计算DTW距离的Reduce函数。
输入:key2值为子矩阵坐标(f,g),list〈value2〉值为计算子矩阵第0行元素集合和第0列元素集合。 输出:结果〈key3,value3〉。
Begin1)for(相同key2值(f,g)对应的list〈value2〉)dobegin2) 获取value2,给子矩阵第0行和第0列赋值; 3) 提取分布式缓存中参与计算子矩阵D(f,g)的子序列Xf和Yg; 4) 计算并记录子矩阵中各DTW距离d[i][j];
5) 将〈key3,value3〉写入HDFS的结果文件: ①key3←本轮迭代计算的子矩阵坐标(f,g);value3←(i,j#d[i][j]);将本次计算的子矩阵结果〈key3,value3〉以“〈(子矩阵分块行号,子矩阵分块列号)(元素行号,元素列号#元素值)〉”的形式(即〈(f,g)(i,j#d[i][j])〉)写入HDFS的结果文件中; ②d[c][j] ←本次计算的子矩阵最后一行元素值;key3←下轮迭代要计算的子矩阵坐标(f+1,g);value3←(0,j#d[c][j]);将下轮迭代计算的子矩阵〈key3,value3〉以“〈(子矩阵分块行号,子矩阵分块列号)(第0行,元素列号#元素值)〉”的形式(即〈(f+1,g)(0,j#d[c][j])〉)写入HDFS的结果文件中; ③d[i][c]←本次计算的子矩阵最后一列元素值;key3←下轮迭代计算的子矩阵坐标(f,g+1);value3←(i,0#d[i][c]);将下轮迭代计算的子矩阵〈key3,value3〉以“〈(子矩阵分块行号,子矩阵分块列号)(元素行号,第0列#元素值)〉”的形式(即〈(f,g+1)(i,0#d[i][c])〉)写入HDFS的结果文件中;end
End
并行计算DTW距离矩阵的主函数迭代地启动Job调用算法2和3的Map/Reduce函数。一轮迭代过程结束则计算完成一条反对角线上的子矩阵块,迭代次数加1,输出路径编号加1。算法采用MapReduce的多目录输出,将要传递的子矩阵最后一行及最后一列与本次计算的子矩阵分开不同目录存放。仅将本次MapReduce的输出路径中存放子矩阵最后一行及最后一列的目录,作为下轮迭代计算的输入目录,从而避免了不必要的数据复制和传递。在Reduce过程中,若出现DTW距离超过阈值,则算法提前结束。所有Reduce写入的子矩阵结果集合即为最终结果的DTW距离矩阵。
2 数据流多模式相似性并行搜索
模式Q与数据流S子序列S[ts,te]之间的DTW距离为d(S[ts,te],Q),起始点位置记为sp(t,i)[8]:
(2)
其中d(t,0)=0,d(0,i)=∞,t=1,2,…,n,i=1,2,…,m。
(3)
从式(2)可看出,若min{d(t,i-1),d(t-1,i-1),d(t-1,i)}>ε且d(t,i)≥0,则d(t,i)>ε,ε为相似性阈值。因此,可以按式(2)裁剪计算,提前排除超出阈值的子序列,以提高搜索效率。
算法4描述了Hadoop平台上时间序列数据流多模式相似性并行搜索(Multi-PatternParallelSearchingOfDistributedStreams,MPPSODS)算法。
算法4MPPSODS算法。
输入:数据流S,模式Q1,Q2,Q3,…。 输出:S中与每个模式相匹配的前k条数据流子序列对应的起止点。Begin1)Map阶段。将数据流分段分配到不同的Map任务中,每个任务在相应的DataNode上采用改进的SPRING算法进行相似性搜索: ①将数据流分段S1,S2,S3,…以及模式Q1,Q2,Q3,…发送到各计算节点上,Map获取计算的数据流分段及其id号、模式及其id号; ②每个节点运行改进的SPRING算法,判断相似性阈值是否符合提前终止的条件; ③将模式id号与每次计算得到的DTW距离连接作为中间结果〈key,value〉中的key,将匹配子序列的起始点、结束点存储在value中。 2) 中间阶段。将所有中间结果〈key,value〉经过一个名为Shuffle的过程,按key值排序并分配给对应的Reducer处理; 3) Reduce阶段。输入的〈key,list〈value〉〉已按从小到大的顺序排列好,分解key中模式id与DTW距离,对于模式id相同的记录只读取前k条记录作为结果输出,同时将前k条记录匹配的数据流子序列对应的起止点写入文件;End
3 实验分析
3.1 实验数据及环境
实验数据来源于“寒区旱区科学数据中心”(http://westdc.westgis.ac.cn)的中国雪深长时间序列数据集(1978—2012)[12-14],将其中的时间序列文件预处理为时间序列的每个数值点占一行,以〈序号,数值〉的形式存储。
Hadoop平台采用通过交换机连接的6台计算机组成分布式并行计算环境,其中每台计算机的内存容量为2GB、处理器为IntelPentiumCPUG2020、主频为2.90GHz,将1台计算机的角色作为主节点(Master)、名称节点(NameNode)和作业跟踪节点(JobTracker),其余5台计算机的角色作为从节点(Slave)、数据节点(DataNode)和任务跟踪节点(TaskTracker),系统网络传输速率为100Mb/s。Hadoop版本为hadoop-1.0.4。运行的操作系统为ubuntu-10.04.4版本。开发环境为Eclipse,采用Java语言编程实现算法。
3.2 实验结果
首先测试并行计算动态时间弯曲距离(PCDTW)算法对运行时间改进的程度。
对于12个不同规模的数据集,当Hadoop平台上参与计算的节点数目逐步增多时,图1给出了PCDTW并行算法和串行算法的运行时间。
从图1的结果可以看出,当时间序列长度小于5 000时,PCDTW并行算法的运行时间多于串行算法的运行时间,且集群中参与计算节点越多反而越耗时。这是因为对于较短的时间序列,需要计算的DTW距离矩阵也相对较小,而每次计算一条反对角线上的子矩阵,都要启动一次Job调用Map/Reduce过程,通信交互和输入输出IO操作都相对耗时。
当每条时间序列的长度达到5 000以上时,在Hadoop上运行PCDTW算法的耗时低于串行算法。时间序列越长,PCDTW算法加速效果越明显。当每条时间序列的长度达到9 000以上时,集群中参与计算的节点越多,PCDTW算法所需运行时间越少。
值得注意的是,当每条时间序列的长度达到8 000以上时,运行串行算法产生内存溢出,无法获得计算结果。

图1 PCDTW算法与串行算法的运行时间
对于时间序列X和Y的长度在10 000以上的数据集A、B、C、D和E,PCDTW算法计算DTW距离矩阵需要的存储容量如表1所示。
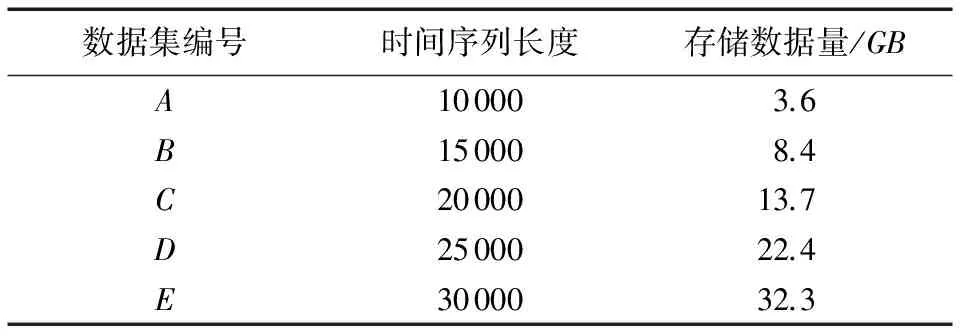
表1 计算DTW距离矩阵需要的存储容量
从表1可知,当时间序列较长时,计算两序列之间的DTW距离矩阵需要较大的存储容量。
图2给出了Hadoop集群中参与计算的节点数目分别为2,3,4,5和6时,PCDTW算法计算数据集A、B、C、D和E的DTW距离所需的时间。
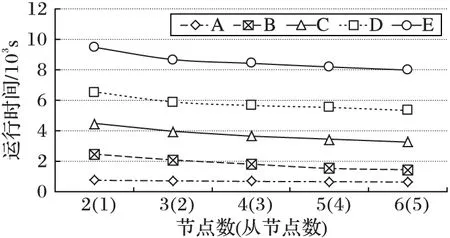
图2 参与计算节点增多时PCDTW算法的运行时间
从图2可以看出,当参与计算的节点数目固定时,时间序列数据集规模越大,PCDTW算法所需时间也越多;对于同一个数据集,当集群中参与计算的节点增多时,PCDTW算法所需时间逐渐减少。这表明,Hadoop平台上并行计算时间序列DTW矩阵的PCDTW算法能够利用集群中不断增多的节点的计算能力。
加速比反映了算法的并行性对运行时间的改进程度。Hadoop集群中参与计算的节点数目分别为2,3,4,5和6时,PCDTW并行算法获得的加速比如图3所示。
图3的结果表明,随着时间序列的增长,PCDTW算法获得的加速比逐渐提高。当每条时间序列长度达到7 000以上时,在Hadoop集群上运行的PCDTW算法加速更加明显。这说明,PCDTW并行算法适用于计算时间序列长、数据集大的动态时间弯曲距离。
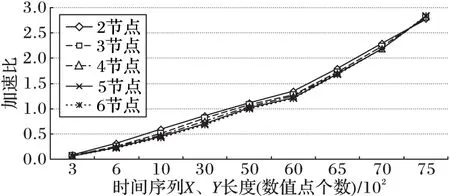
图3 参与计算节点增多时PCDTW算法的加速比
为了测试数据流多模式相似性搜索并行算法MPPSODS相对于串行算法STRING运行时间的改进程度,将包含25 000个数据点的数据流划分为5段,依次对表2中的H、I、J和K这4组模式集中每组的3个模式(查询序列)进行并行搜索,算法所需的运行时间如图4所示。
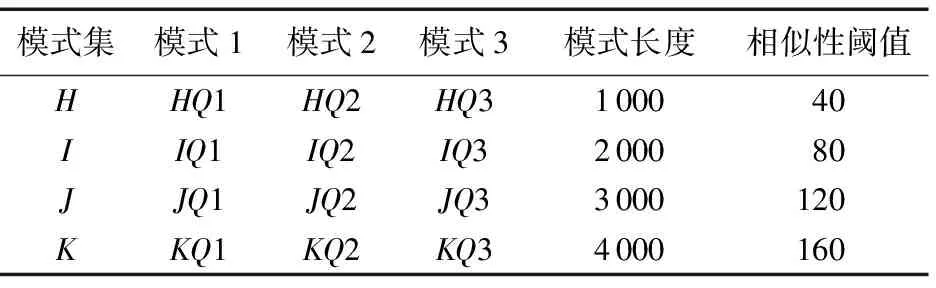
表2 模式(查询序列)集及相似性阈值
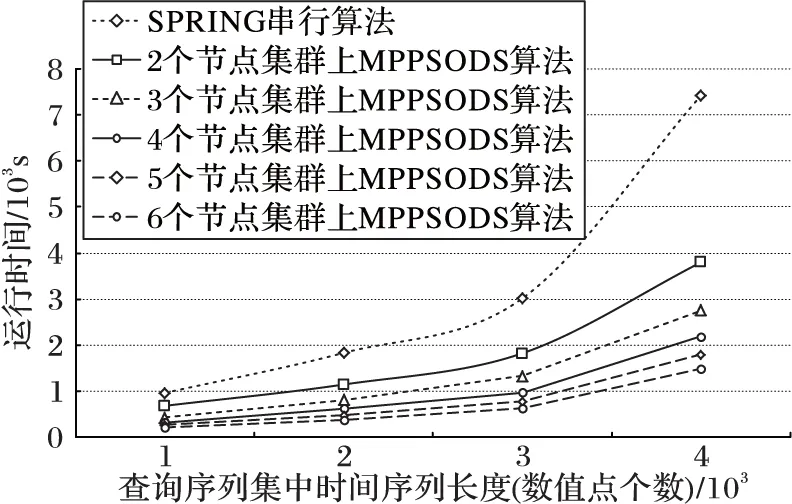
图4 MPPSODS算法与串行算法的运行时间
从图4中可看出,随着模式(查询序列)中时间序列长度的增大,并行算法MPPSODS和串行算法SPRING搜索时间也随之增长,但SPRING算法所需的运行时间增长较快,而MPPSODS算法的运行时间增长较为缓慢,且Hadoop集群中参与计算的节点越多,MPPSODS算法运行时间越少。
对于H、I、J和K这4组模式(查询序列),图5给出了Hadoop集群参与计算的节点增多时,MPPSODS算法的运行时间。
图5的结果表明,对于同一组模式(查询序列),随着Hadoop集群中参与计算的节点增多,MPPSODS算法运行时间逐渐减少;而且模式越长、参与计算的节点越多,MPPSODS算法所需时间越少。这说明,MPPSODS算法有效利用了Hadoop集群中逐步增多的节点的计算能力。
图6~8分别给出MPPSODS算法对模式(查询序列)集H中3条序列HQ1、HQ2、HQ3进行相似性搜索得到的结果。
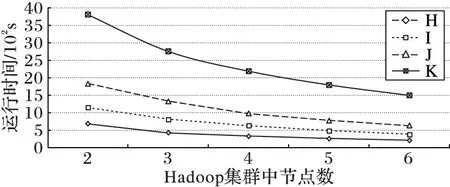
图5 参与计算节点增多时MPPSODS算法的运行时间
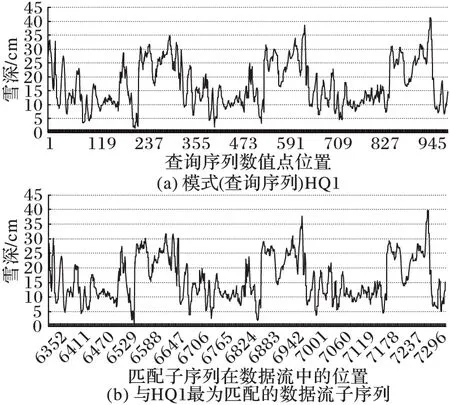
图6 MPPSODS算法对HQ1搜索的结果

图7 MPPSODS算法对HQ2搜索的结果
从图6可以看到,在数据流上搜索出与模式(查询序列)HQ1最为匹配的数据流子序列的开始位置为6 362、结束位置为7 337、长度为986。
从图7可以看到,在数据流上搜索出与模式(查询序列)HQ2最为匹配的数据流子序列的开始位置为2 008、结束位置为3 001、长度为994。
从图8可以看到,在数据流上搜索出与模式(查询序列)HQ3最为匹配的数据流子序列的开始位置为11 455、结束位置为12 425、长度为971。
图6~8的结果表明,MPPSODS算法并行搜索数据流得到匹配的子序列与模式(查询序列)在形态上具有很高的相似性。
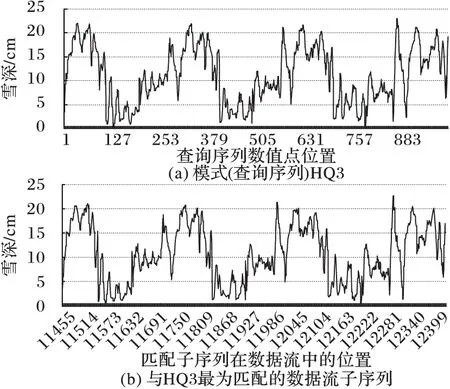
图8 MPPSODS算法对HQ3搜索的结果
4 结语
时间序列数据流具有连续、实时和无限制特性。大数据环境下长时间序列的动态弯曲距离计算和数据流多模式相似性搜索相当耗时,并行求解算法提供了有效的解决方案。基于Hadoop平台和MapReduce编程模型,本文设计实现的并行算法能够利用集群中不断增加的节点的计算能力,高效地计算动态时间弯曲距离和从数据流中搜索出与模式相似的子序列,所得到的匹配子序列与模式序列在形态上具有很高的相似性。下一步的工作将在Hadoop平台上开发一个时间序列数据流多模式相似性并行搜索软件包供人们在线使用。
References)
[1] MATSUBARA Y, SAKURAI Y, FALOUTSOS C, et al.Fast mining and forecasting of complex time-stamped events [C]// Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York: ACM, 2012: 271-279.
[2] WANG L, LEEDHAM G.Near and far infrared imaging for vein pattern biometrics [C]// Proceedings of the 2006 IEEE International Conference on Video and Signal Based Surveillance.Piscataway, NJ: IEEE, 2006: 52-52.
[3] 陈乾,胡谷雨.一种新的DTW最佳弯曲窗口学习方法[J].计算机科学,2012,39(8):191-195.(CHEN Q, HU G Y.New leaning method for optimal warping window of DTW [J].Computer Science, 2012, 39(8): 191-195.)
[4] 莫倩芸,钟诚.机群系统上并行计算时间序列的动态弯曲距离[J].微电子学与计算机,2008,25(10):155-158.(MO Q Y, ZHONG C.Parallel computing dynamic warping distances for time sequences on the cluster computing systems [J].Microelectronics & Computer, 2008, 25(10): 155-158.)
[5] 张建平,李斌,刘学军,等.基于Hadoop的不确定异常时间序列检测[J].传感技术学报,2014,27(12):1659-1665.(ZHANG J P, LI B, LIU X J, et al.Uncertain abnormal time series detection based on Hadoop [J].Chinese Journal of Sensors and Actuators, 2014, 27(12): 1659-1665.)
[6] 沙剑.基于GPU的时间序列并行检索算法研究[D].大连:大连理工大学,2011:42-55.(SHA J.The research on parallel time series retrieval method based on GPU [D].Dalian: Dalian University of Technology, 2011: 42-55.)[7] 欧阳一村.基于DTW距离的两步式时间序列相似搜索[D].广州:中山大学,2010:33-54.(OUYANG Y C.Two-step similarity search of time series based on DTW distance [D].Guangzhou: Sun Yat-sen University, 2010: 33-54.)
[8] SAKURAI Y, FALOUTSOS C, YAMAMURO M.Stream monitoring under the time warping distance [C]// Proceedings of the 23rd International Conference on Data Engineering.Piscataway, NJ: IEEE, 2007: 1046-1055.
[9] TOYODA M, SAKURAI Y, ISHIKAWA Y.Pattern discovery in data streams under the time warping distance [J].VLDB Journal, 2013, 22(3): 295-318.
[10] SRIRAMA S N, JAKOVITS P, VAINIKKO E.Adapting scientific computing problems to clouds using MapReduce [J].Future Generations Computer System, 2012, 28(1): 184-192.
[11] 钟诚,陈国良.PRAM和LARPBS模型上的近似串匹配并行算法[J].软件学报,2004,15(2):159-169.(ZHONG C, CHEN G L.Parallel algorithms for approximate string matching on PRAM and LARPBS [J].Journal of Software, 2004, 15(2): 159-169.)
[12] 寒区旱区科学数据中心.中国雪深长时间序列数据集(1978—2012) [EB/OL].[2014-09-28].http://westdc.westgis.ac.cn.(Cold and Arid Regions Science Data Center at Lanzhou.Snow depth long time series data set in China (1978—2012) [EB/OL].[2014-09-28].http://westdc.westgis.ac.cn.)
[13] CHE T, LI X, JIN R, et al.Snow depth derived from passive microwave remote-sensing data in China [J].Annals of Glaciology, 2008, 49(1): 145-154.
[14] DAI L, CHE T, WANG J, et al.Snow depth and snow water equivalent estimation from AMSR-E data based on a priori snow characteristics in Xinjiang, China [J].Remote Sensing of Environment, 2012, 127: 14-29.
This work is supported by the Natural Science Foundation of Guangxi (2014GXNSFAA118396).
FU Chen, born in 1988, M.S.Her research interests include network software engineering, high-performance computing for big data.
ZHONG Cheng, born in 1964, Ph.D., professor.His research interests include high-performance computing for big data, network software engineering.
YE Bo, born in 1974, Ph.D., senior engineer.His research interests include network software engineering, management information system.
Accelerating parallel searching similar multiple patterns from data streams by using MapReduce
FU Chen1, ZHONG Cheng1*, YE Bo2
(1.SchoolofComputer,ElectronicsandInformation,GuangxiUniversity,NanningGuangxi530004,China;2.GuangxiScientificandTechnologicalInformationCenter,NanningGuangxi530012,China)
The effective storage mode for time series was designed on Hadoop Distributed File System (HDFS), the sub-series were distributed to the compute nodes on Hadoop cluster by applying Distributed Cache tool, and the matrix of dynamic time warping distances was partitioned into several sub-matrixes.Based on MapReduce programming mode, by parallel computing sub-matrixes in each back-diagonal iteratively, the parallel computation of dynamic time warping distances was implemented, and an efficient parallel algorithm for searching similar patterns from data streams was developed by improving pruning redundant computation.The experimental results on the data set of snow depth long time series in China show that when the length of each time series is equal to or longer than 5 000, the required time of parallel computing dynamic time warping distances is less than that of the corresponding sequential computation, and when the length of each time series is equal to or longer than 9 000, the more the compute nodes used, the less the required parallel computation time; furthermore, when the length of each pattern is equal to or longer than 4 000 and the number of compute nodes is equal to or larger than 5, the required time of parallel searching similar sub-series from data streams is 20% of the corresponding sequential searching time.
time series; data stream; dynamic time warping distance; pattern searching; Hadoop
2016-08-25;
2016-09-03。 基金项目:广西自然科学基金资助项目(2014GXNSFAA118396)。
付晨(1988—),女,江西瑞昌人,硕士,主要研究方向:网络软件工程、大数据高性能计算; 钟诚(1964—),男,广西桂平人,教授,博士,CCF高级会员,主要研究方向:并行计算、大数据高性能计算、网络软件工程; 叶波(1974—),男,广西南宁人,教授级高级工程师,博士,主要研究方向:网络软件工程、管理信息系统。
1001-9081(2017)01-0037-05
10.11772/j.issn.1001-9081.2017.01.0037
TP338.6; TP301.6
A
